怎么绘制y=x^(1-x)的图像？

1、这里用到的工具，都是有相应的网页版的。

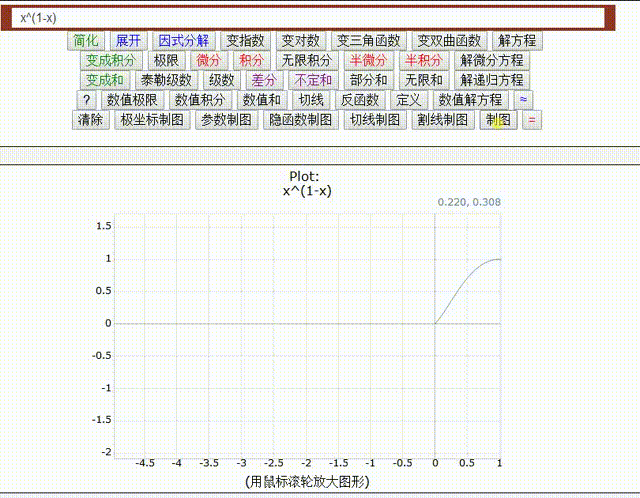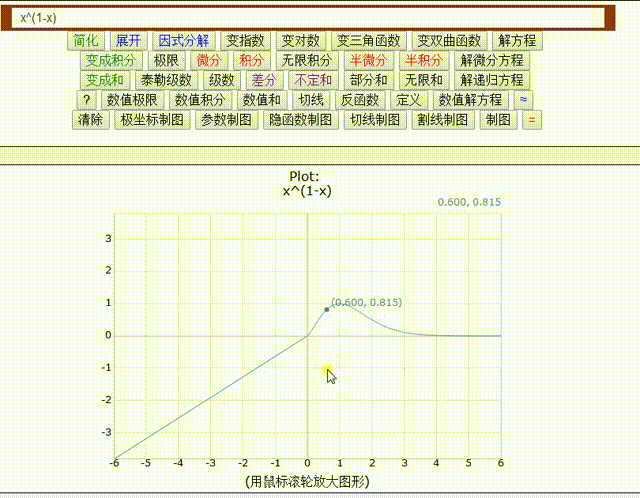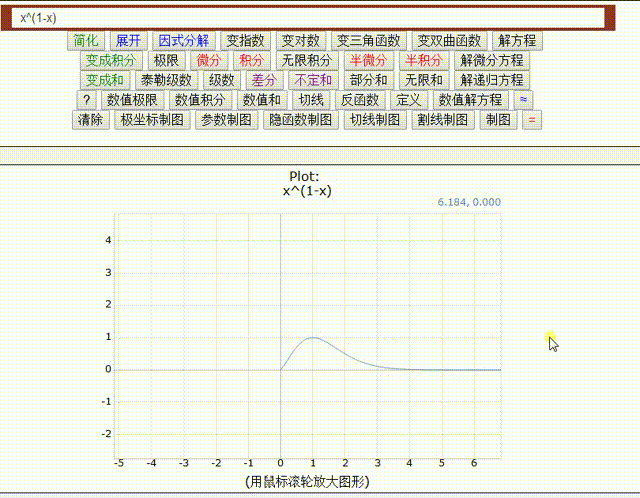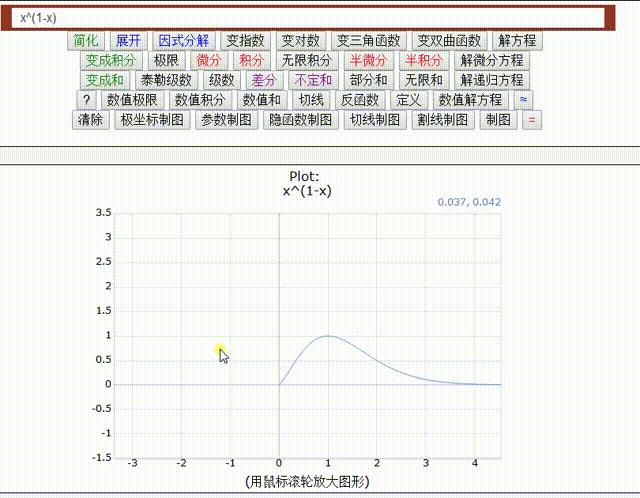
用数学手册计算器，可以不用指定绘图区间。

注意看图像，在第三象限居然也有存在，但是稍微拖动一下，那第三象限的图像就消失了。

这说明，图像在第三象限只是若干散点。

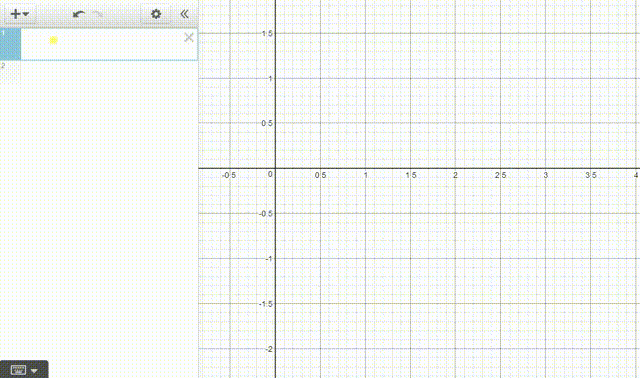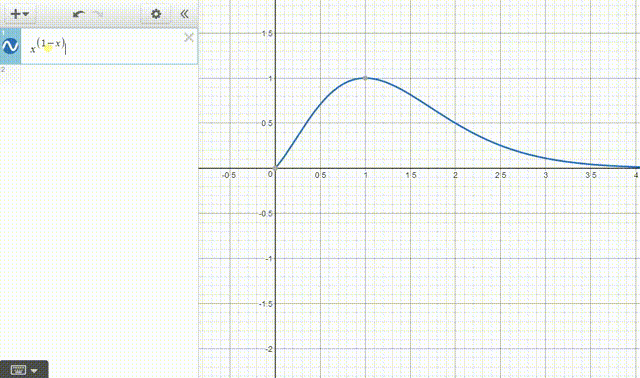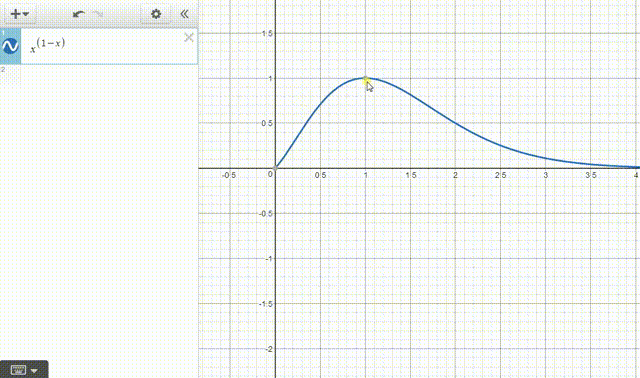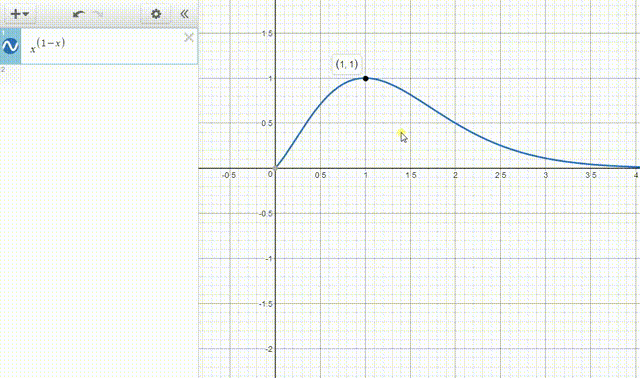
2、Desmos也不需要指定绘图区间。

x^{\left(1-x\right)}

Desmos还自动给出了函数的极值点的位置。

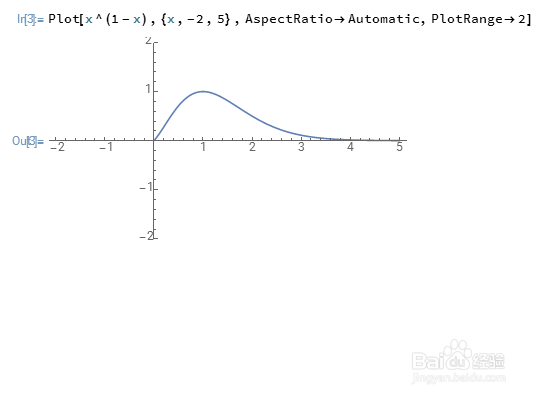
3、Mathematica绘图，需要指定绘图区间：

Plot[x^(1-x),{x,-2,5},AspectRatio->Automatic,PlotRange->2]

4、而网络画板得到的图像，则是把x<0的部分的散点图用折线连接在一起了。

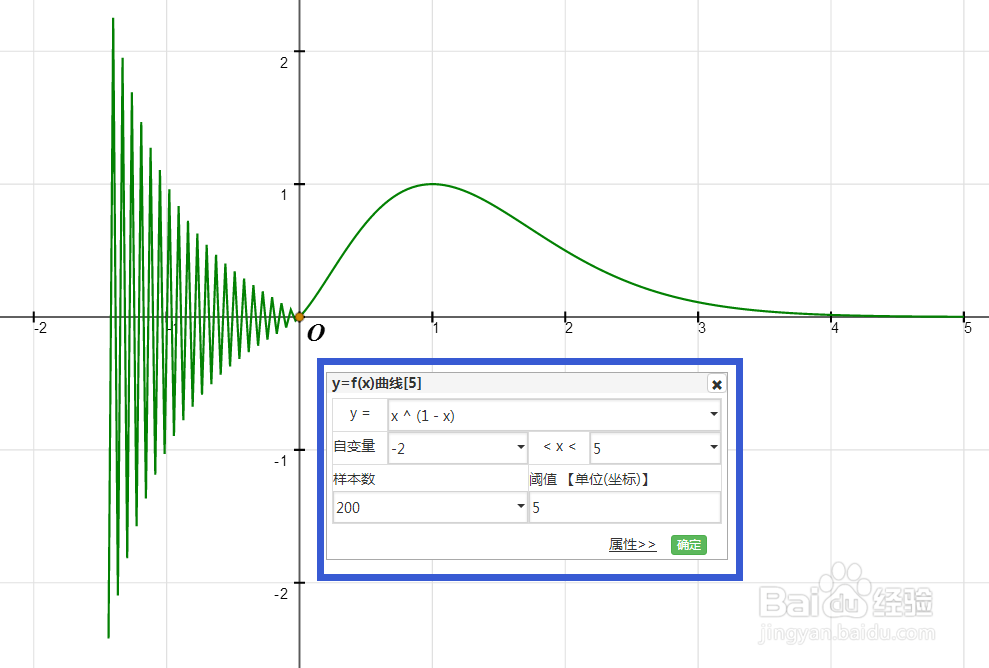
1、下面，我们专门使用Mathematica研究x<0的情况。

如果要限定y是实函数，那么我们知道，图像只能是散点图:

Table[{x,x^(1-x)},{x,0,-2,-1}]

ListPlot[%8,PlotStyle->Blue,Filling->Axis]

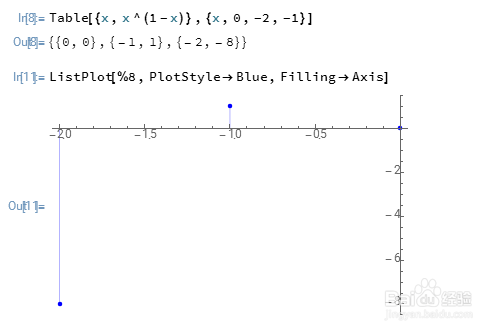
2、当x=-1/3的时候，x^(1-x)=(-1/3)^(2/3)，这个式子，在Mathematica看来，应该是一个复数。

然而，这个(-1/3)^(2/3)在实数范围内是存在的。

3、如果按照Mathematica默认的算法，(-1/3)^(2/3)是复数，我们尝试着在复平面上作图这些散点图：

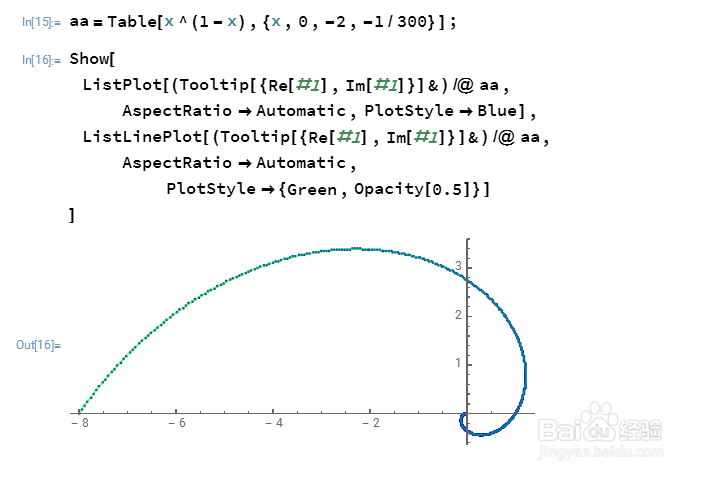
aa=Table[x^(1-x),{x,0,-2,-1/3}];

ListPlot[(Tooltip[{Re[#1],Im[#1]}]&)/@aa,       AspectRatio->Automatic,PlotStyle->Blue]

4、把散点的间隔变小一点：

aa=Table[x^(1-x),{x,0,-2,-1/300}];

ListPlot[(Tooltip[{Re[#1],Im[#1]}]&)/@aa,       AspectRatio->Automatic,PlotStyle->Blue]