【尺规作图】怎么单尺确定相交两圆的圆心？

1、首先，提供主要的核心理论依据：

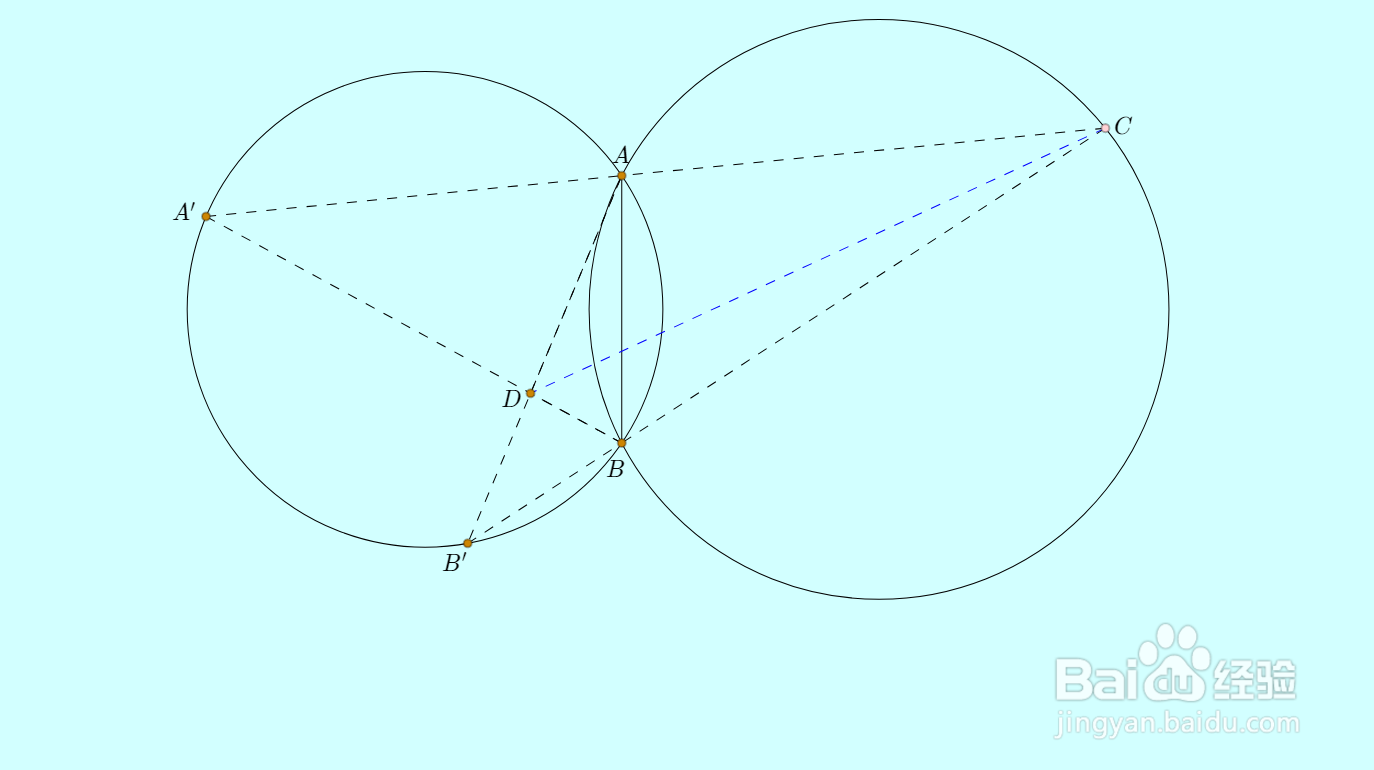
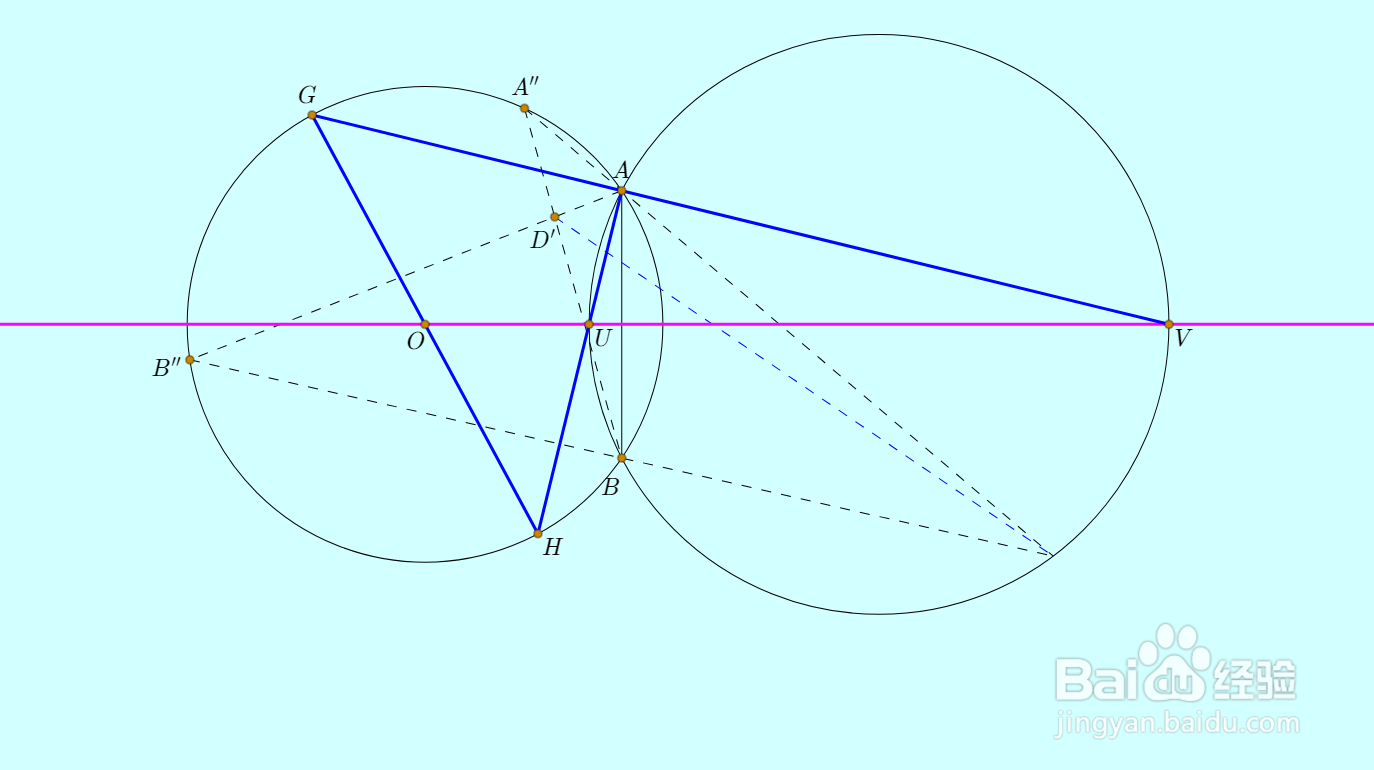
假设C是右圆上的任意一点，直线CA、CB分别交左圆于A'、B'点；

直线AB'和BA'交于D点，那么直线CD过定点。

2、再来证明上面的核心理论依据：

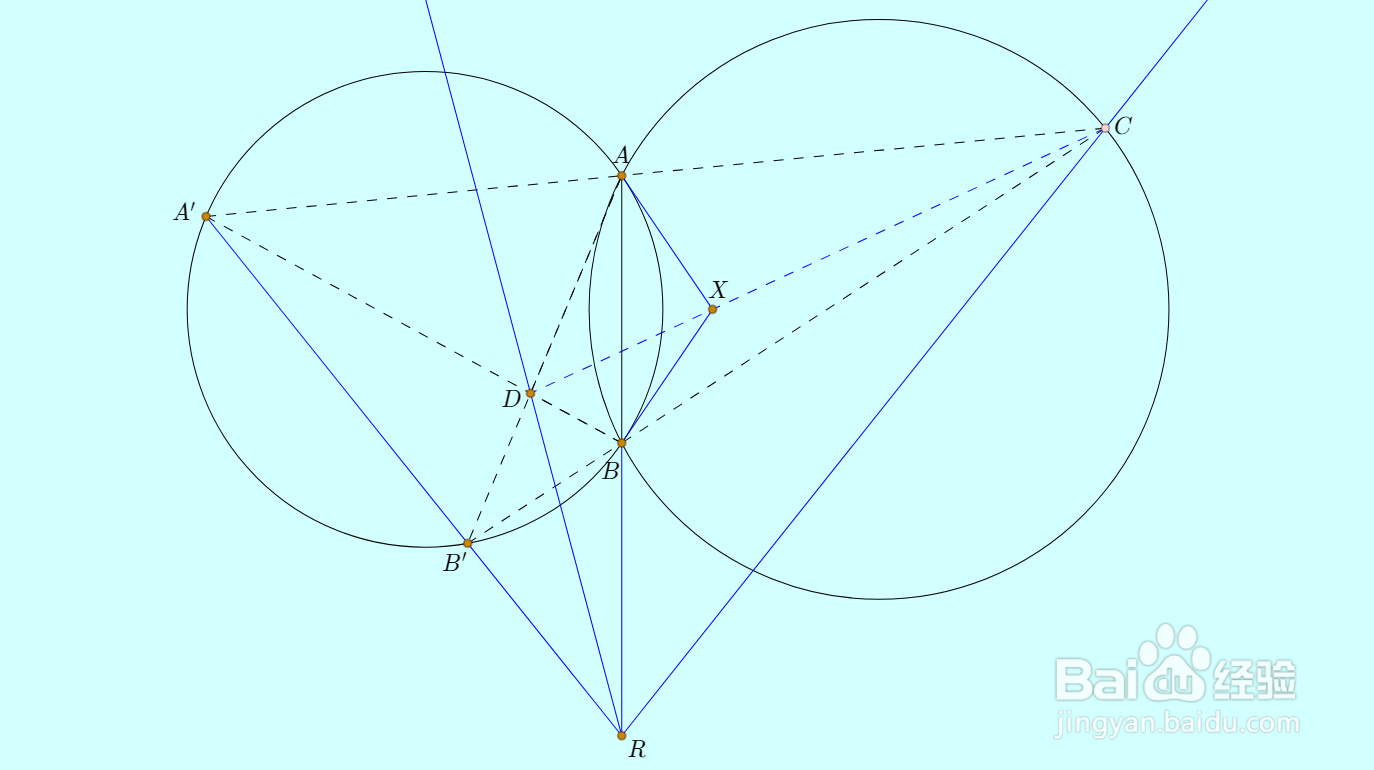
AX、BX是左圆的切线；

直线AB和A'B'的交点记为R；

D关于左圆的极线是RC；

C关于左圆的极线是RD；

X关于左圆的极线是RA；

因为三条极线共点于R，所以C、D、X三点共线。

这就说明，直线CD恒过点X。

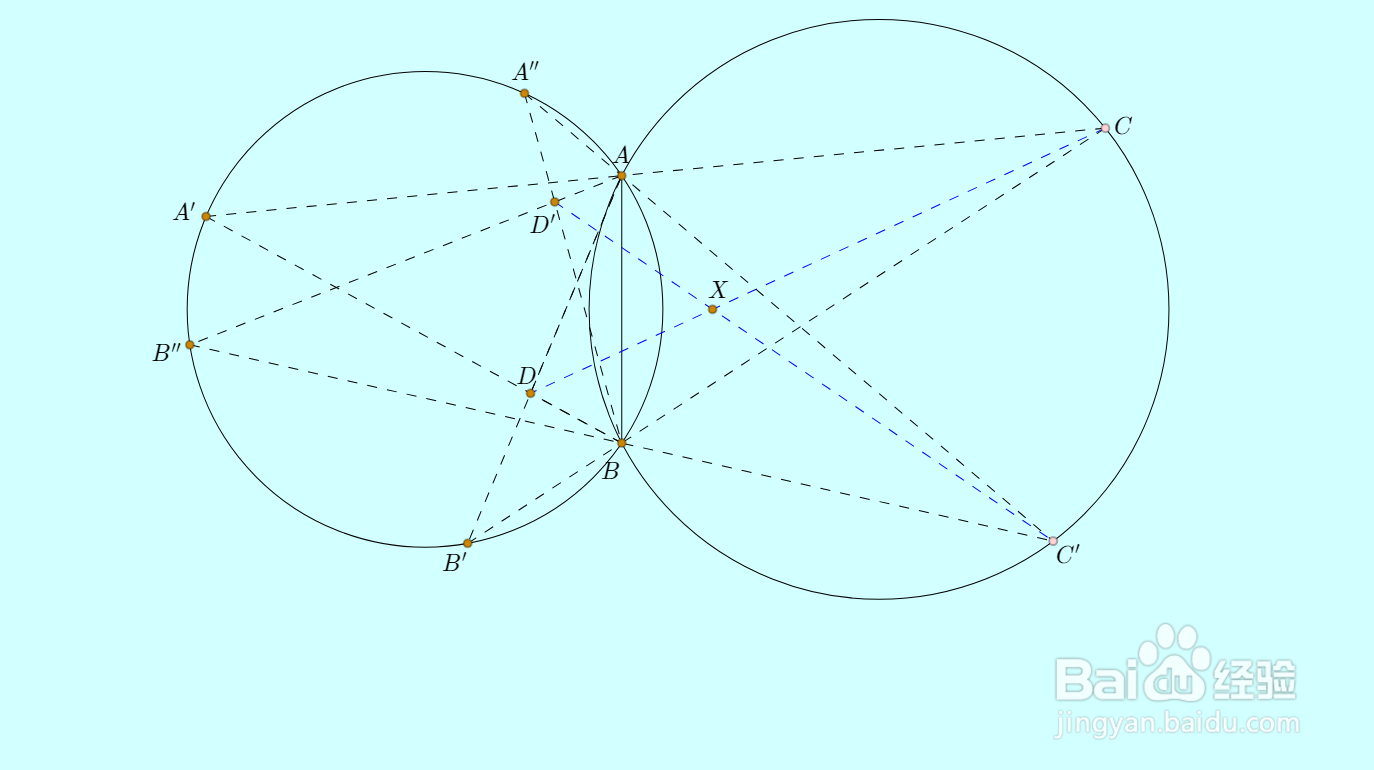
3、在右圆上取另一个点C'，作出C'D'，与CD的交点，就是上述定点X。

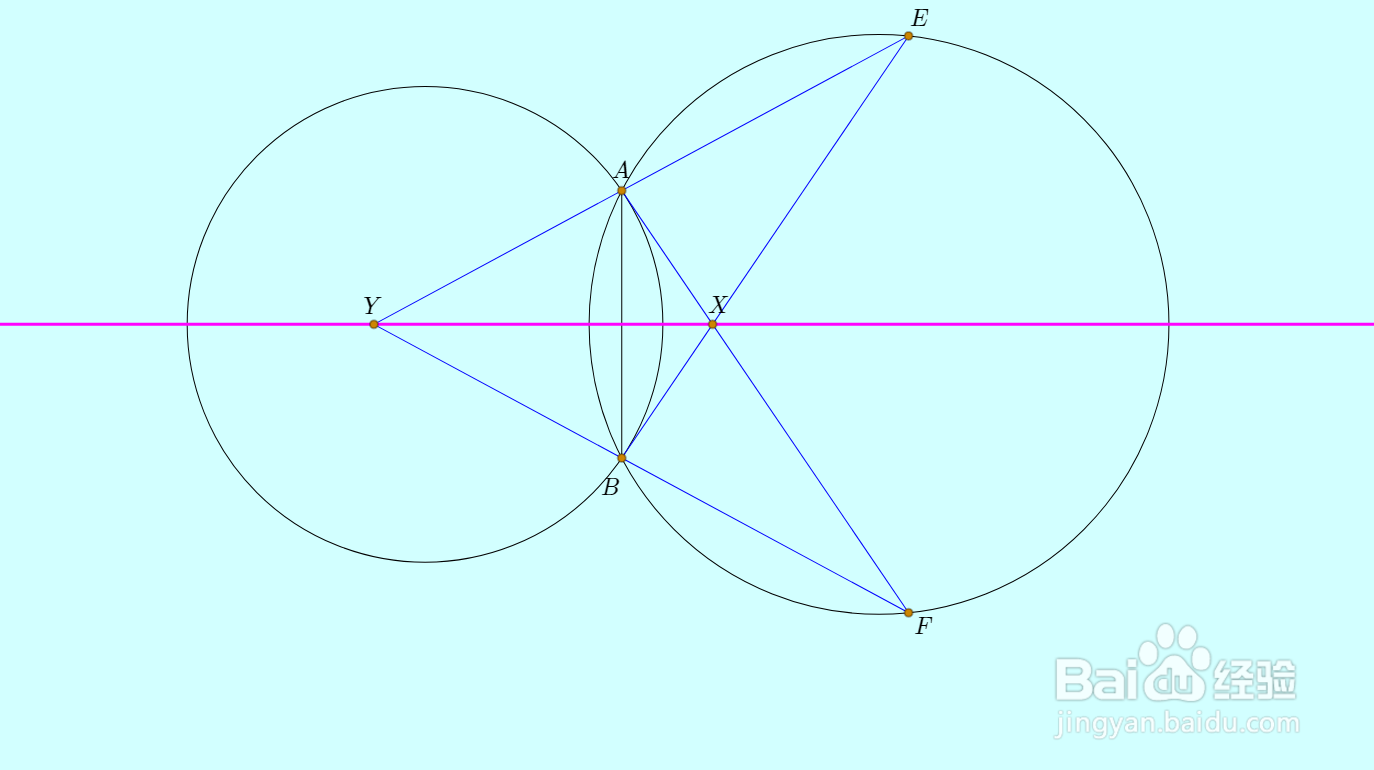
4、这个X点一定在两圆连心线上；

A、B关于连心线对称；

直线AX、BX与右圆的另一个交点记为F、E，那么E、F关于连心线对称；

EA和FB交于Y点，那么Y就在连心线上。

连接直线XY，就是连心线。

5、连心线与右圆交于U、V两点，那么UV就是直径，∠VAU是直角。

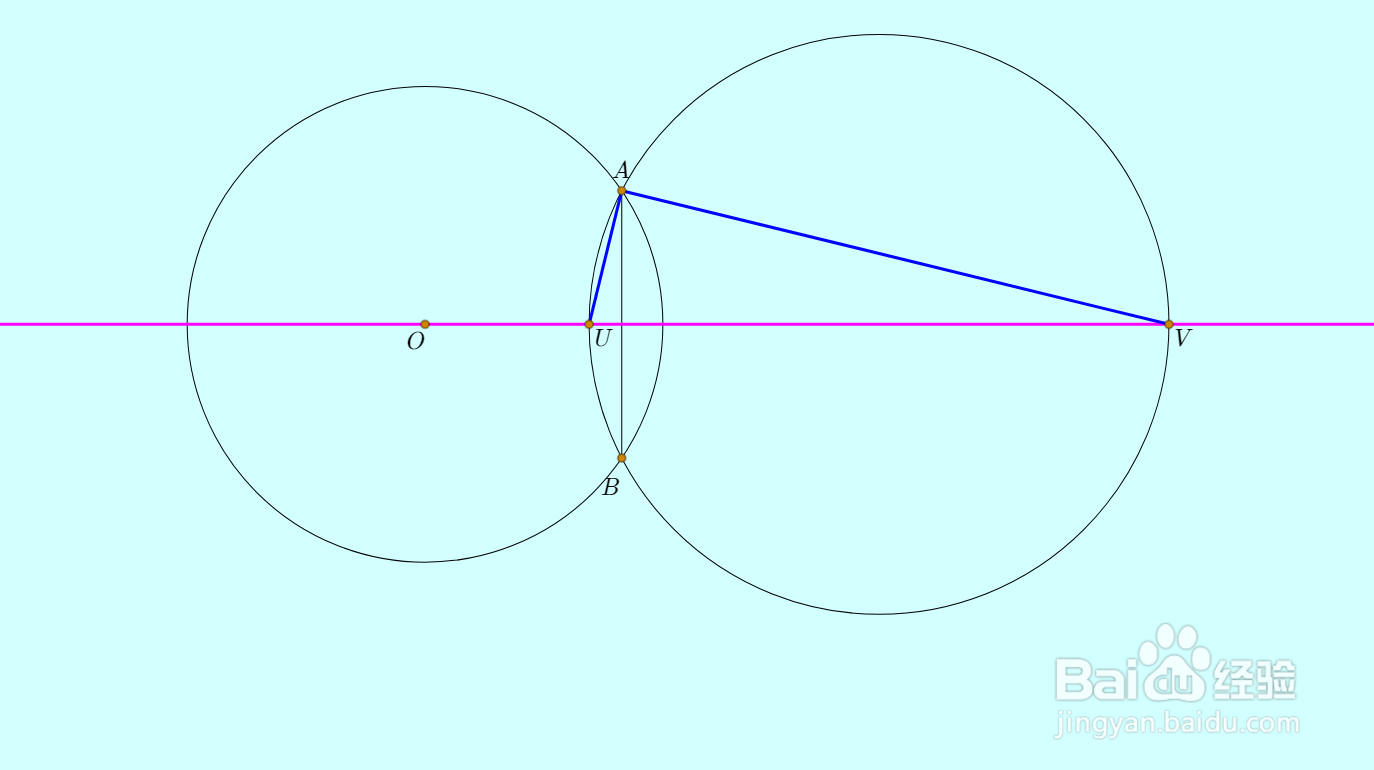
6、直线VA、UA与左圆交于另一个点G、H，那么GH就是左圆的直径；

GH与连心线的交点O，就是左圆的圆心。

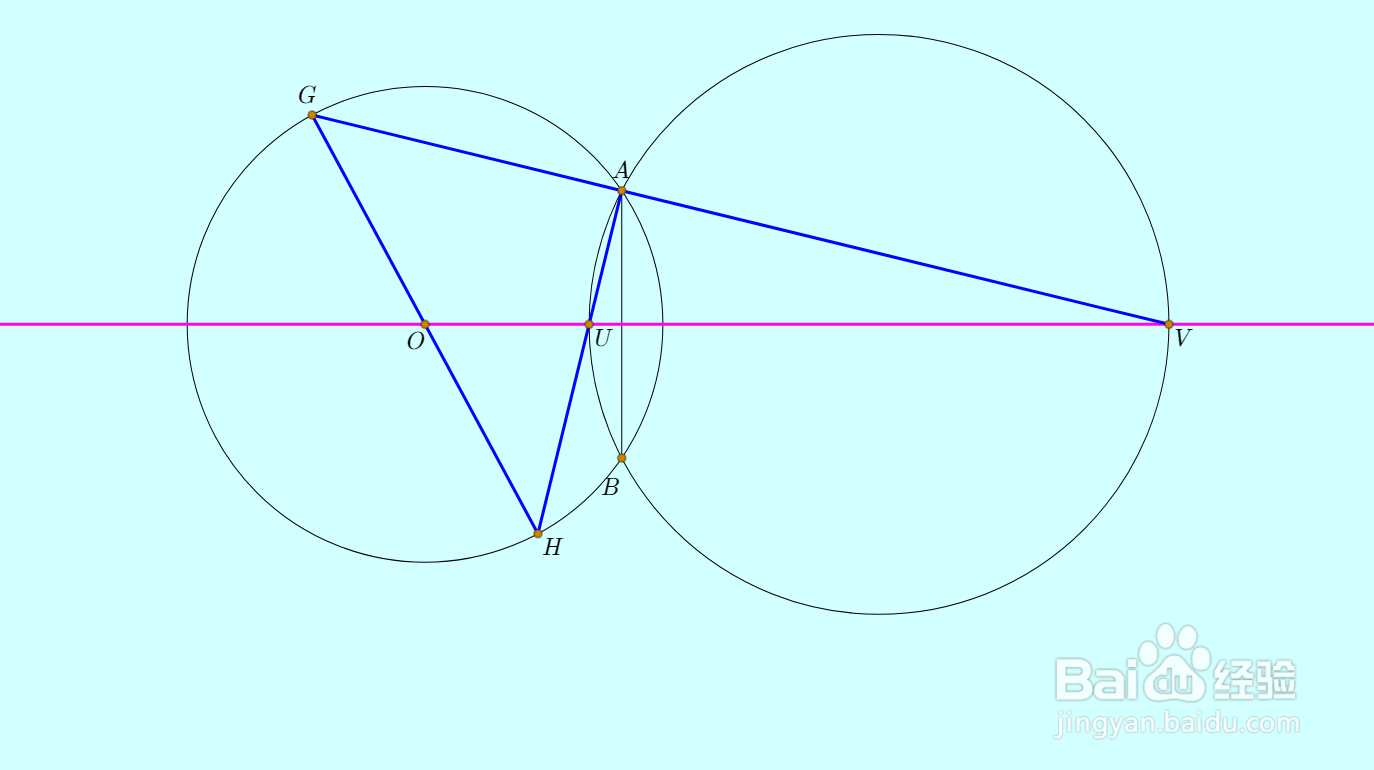
7、再留一个思考题：

如果只画出线段AB，能不能单尺确定线段AB的中点？