用Mathematica玩转莫比乌斯带
1、 莫比乌斯带的参数方程是:x=cost(3+r*cos(t/2)),y=sint(3+r*cos(t/2)),z=r*sin(t/2)。其中,r代表的是莫比乌斯带的宽度。
用Mathematica画出图形,可以使用ParametricPlot3D:
ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]),
r Sin[t/2]}, {r, -1, 1}, {t, 0, 2 Pi}
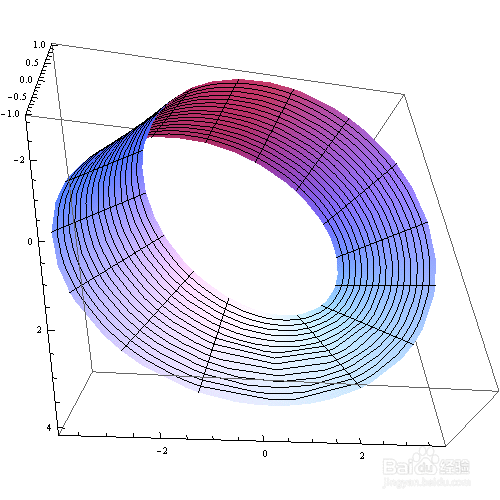
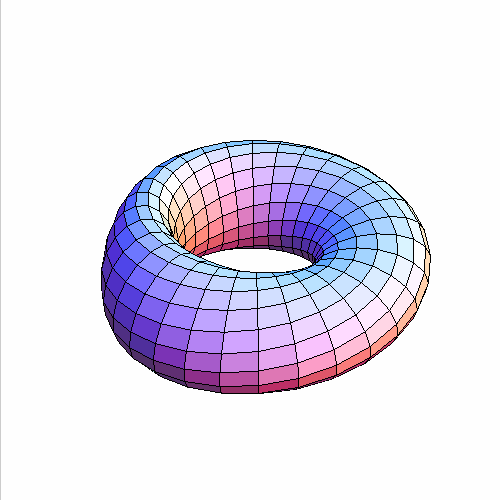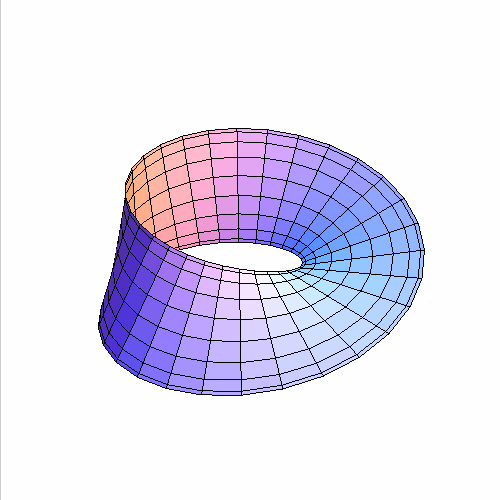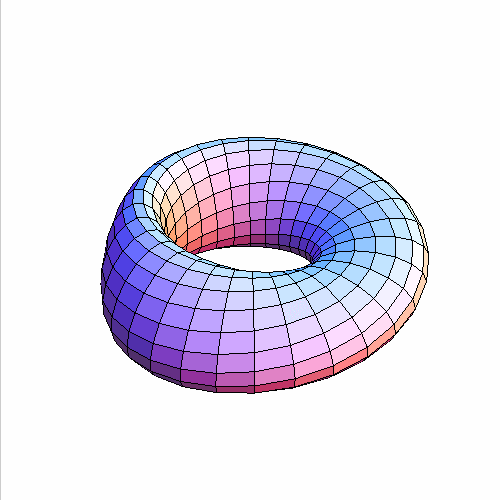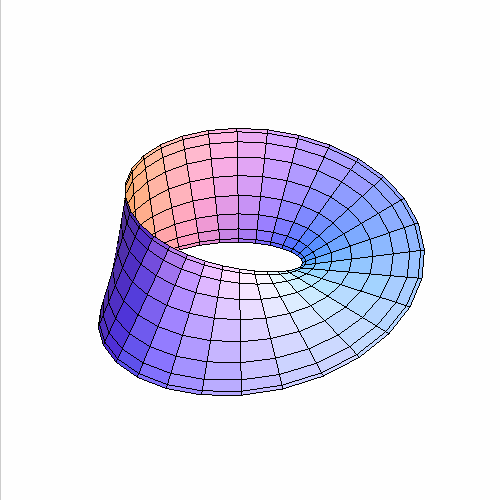
2、 把坐标轴、外框、网格线都去掉,代码如下:
ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]),
r Sin[t/2]}, {r, -1, 1}, {t, 0, 2 Pi}, Axes -> False, Mesh -> None,
Boxed -> False

3、 我一直好奇,如果莫比乌斯带很宽,当年Mobius还有可能扭出这个单侧曲面吗?让我们来看看r很大的时候,莫比乌斯带长什么模样!
ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]),
r Sin[t/2]}, {r, -2,2}, {t, 0, 2 Pi}, Axes -> False, Mesh -> None,
Boxed -> False
和
ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]),
r Sin[t/2]}, {r, -6,6}, {t, 0, 2 Pi}, Axes -> False,
Mesh -> None, Boxed -> False

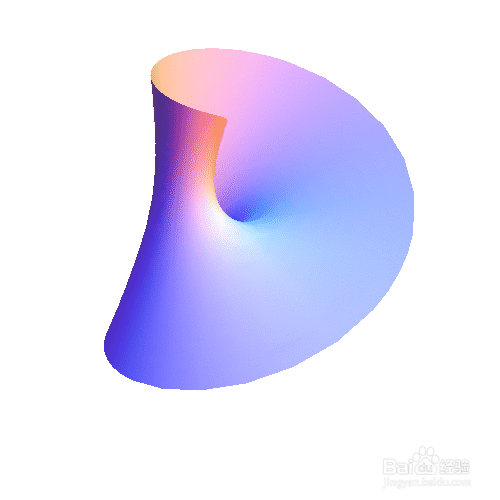
4、 把上面的过程,变成互动模型:
Clear[a];
Manipulate[
ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]),
r Sin[t/2]}, {r, -a, a}, {t, 0, 2 Pi}, Axes -> False, Mesh -> None,
Boxed -> False], {a, 1, 30}
或者导出为动态图:
Export["C:\\Users\\Administrator\\Desktop\\a.gif",
Table[ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]),
Sin[t] (3 + r Cos[t/2]), r Sin[t/2]}, {r, -a, a}, {t, 0, 2 Pi},
Axes -> False, Mesh -> None, Boxed -> False,
], {a, 1, 30}]


5、 用ColorFunction改变颜色:
Manipulate[
ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]),
r Sin[t/2]}, {r, -a, a}, {t, 0, 2 Pi}, Axes -> False, Mesh -> None,
Boxed -> False, ColorFunction -> Function[{t, r}, Hue[t]]], {a, 1, 30}]
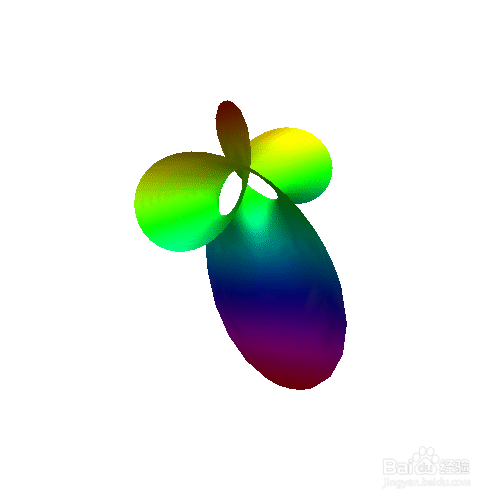
6、 把第五步的互动效果输出为动态图,代码如下:
Export["C:\\Users\\Administrator\\Desktop\\a.gif",
Table[ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]),
Sin[t] (3 + r Cos[t/2]), r Sin[t/2]}, {r, -a, a}, {t, 0, 2 Pi},
Axes -> False, Mesh -> None, Boxed -> False,
ColorFunction -> Function[{t, r}, Hue[t]]], {a, 1, 30}]]
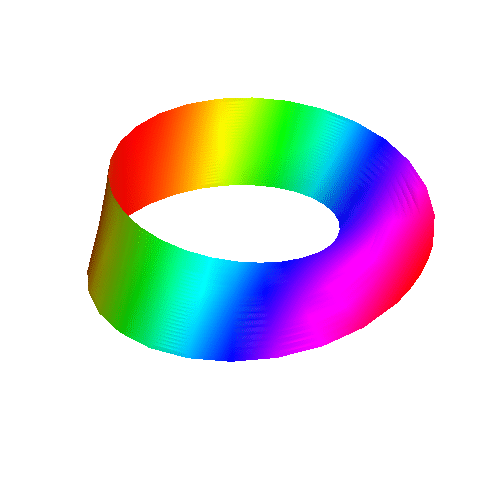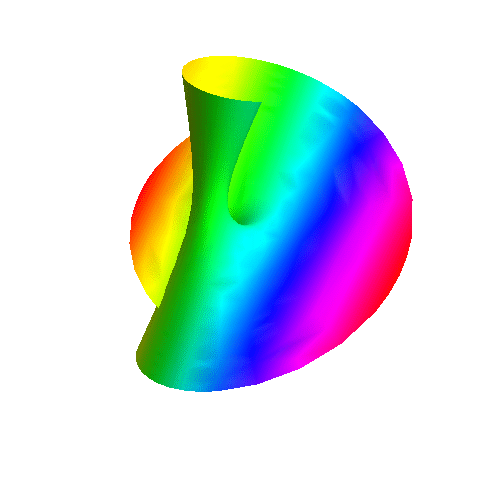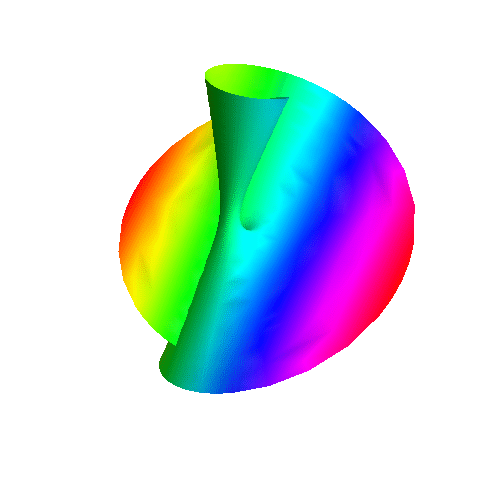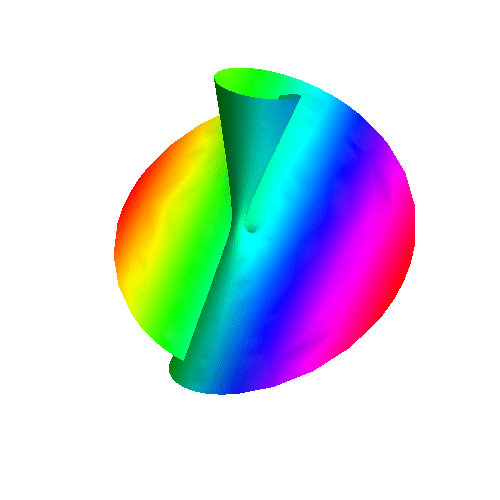
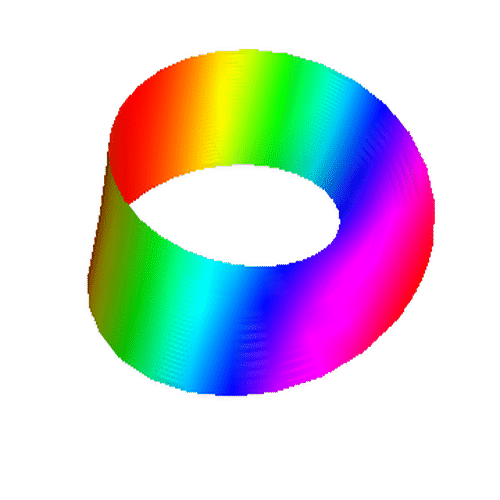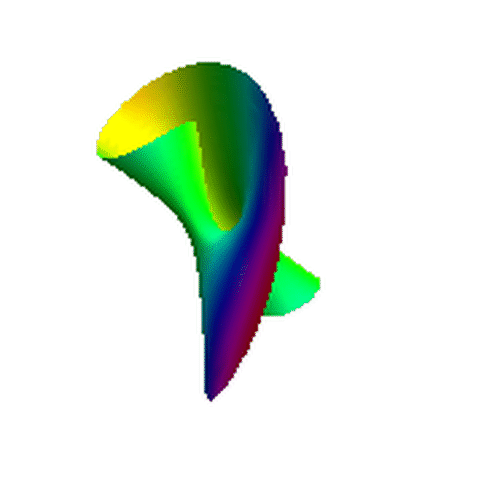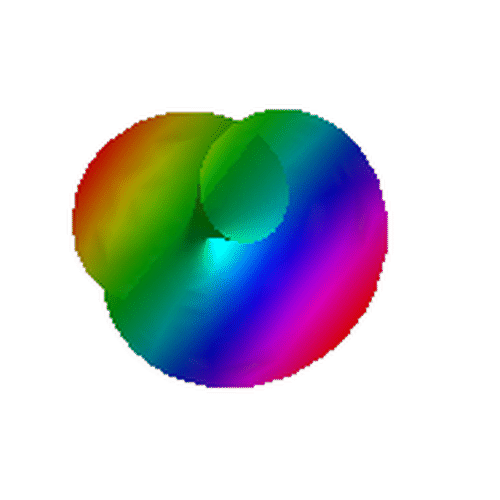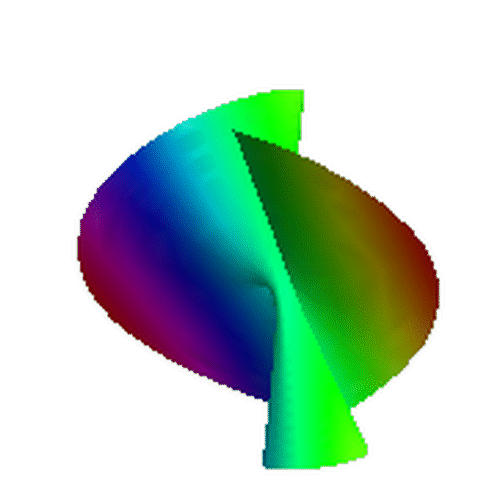
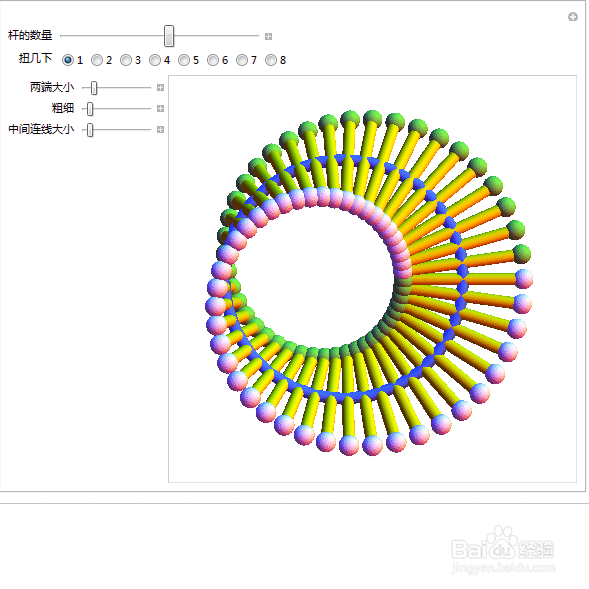
7、 用旋转的杆来扭出一个莫比乌斯带,并生成互动效果,代码有点长:
Manipulate[
c1 = {Yellow, Cylinder[{{-1, 0, 0}, {1, 0, 0}}, diac]};
s1 = Sphere[{-1, 0, 0}, dias];
s2 = {RGBColor[0.5, 1, 0.3], Sphere[{1, 0, 0}, dias]};
m1 = Table[
Rotate[Translate[
Rotate[{c1, s1, s2}, i fr Pi/n, {0, 1, 0}], {2, 0, 0}],
i 2 Pi/n, {0, 0, 1}], {i, n}];
tor = {RGBColor[0.3, 0.5, 1],
ParametricPlot3D[{(2 + diat Cos[u]) Cos[v], (2 + diat Cos[u]) Sin[
v], diat Sin[u]}, {u, 0, 2 Pi}, {v, 0, 2 Pi}, Mesh -> None,
MaxRecursion -> 1][[1]]};
Graphics3D[{m1, tor}, ViewAngle -> \[Pi]/15, SphericalRegion -> True,
Boxed -> False, ViewPoint -> {0, 0, 5}, ImageSize -> {380, 380}],
{{n, 50, "杆的数量"}, 2, 80, 1},
{{fr, 1, "扭几下"}, 1, 8, 1, RadioButton},
{{dias, 0.17, "两端大小"}, 0.02, 1, ImageSize -> Tiny,
ControlPlacement -> Left},
{{diac, 0.1, "粗细"}, 0.02, 1, ImageSize -> Tiny,
ControlPlacement -> Left},
{{diat, 0.1, "中间连线大小"}, 0.02, 1, ImageSize -> Tiny,
ControlPlacement -> Left}, TrackedSymbols -> Manipulate

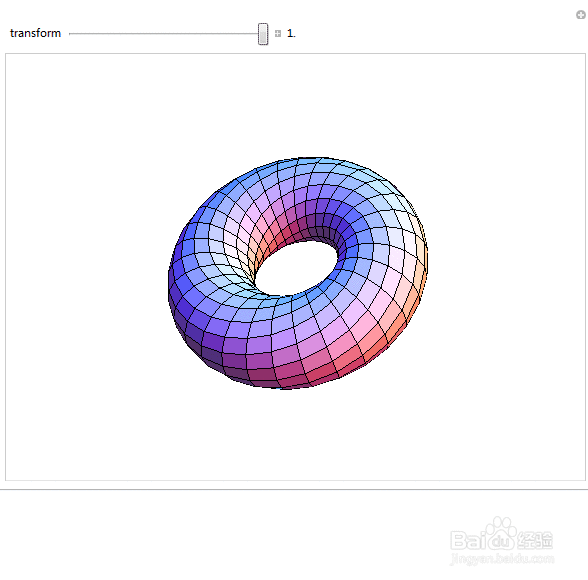
8、 莫比乌斯带能够膨胀成为一个“轮胎”,当然前提是,莫比乌斯带本身没有自相交:
makeShape[vl_List, c1_Integer, c2_Integer] :=
Block[{l = vl,
l1 = RotateLeft /@ vl,
mesh},
mesh = {l, l1, RotateLeft[l1], RotateLeft[l]};
If[c1 == 1, mesh = Map[Drop[#, -1] &, mesh, {1}] ];
If[c2 == 1, mesh = Map[Drop[#, -1] &, mesh, {2}] ];
Polygon /@ Transpose[ Map[Flatten[#, 1] &, mesh] ] (*]*)
] /; TensorRank[vl] >= 2;
Manipulate[
Graphics3D[
makeShape[
Table[{Cos[u], Sin[u], 0} +
0.5 Cos[v] { Cos[u/2] Cos[u], Cos[u/2] Sin[u],
Sin[u/2]} + .5 a Sin[v] { -Sin[u/2] Cos[u], -Sin[u/2] Sin[u],
Cos[u/2]}, {u, 0., 2 Pi, 2 Pi/30}, {v, 0, 2 Pi, 2 Pi/18}], 1,
1], Boxed -> False, ImageSize -> {550, 400},
SphericalRegion -> True] , {{a, 0.1, "transform"}, 0.0, 1.0, 0.1,
Appearance -> "Labeled"}, SaveDefinitions -> True,
ControlPlacement -> Top
9、 这说明,圆环无论怎么扭,都不会变成“克莱因瓶”。最后,画个克莱因瓶看看!
Manipulate[
With[{bsc = Take[{{0, 0, 0}, {0, 0, 14}, {0, 0, 20}, {0, 0, 25},
{1.7, 0, 30}, {7, 0, 32}, {10, 0, 31.5}, {13, 0,
30}, {15, 0, 26},
{13, 0, 20}, {10, 0, 17.5}, {4, 0, 13.5}, {2.5, 0,
11}, {0.33, 0, 7},
{0.2, 0, 2.5}, {0, 0, 0}}, t + 2],
sizes =
Take[{6.5, 14, 4, 2.3, 2.2, 2.2, 2.2, 2.2, 2.2, 2.2, 2.2, 2.6,
3.3, 3.6,
4.3, 6.5}, t + 2]},
Graphics3D[{color, CapForm[None], Opacity[opacity],
Tube[BSplineCurve[bsc], sizes]}, Boxed -> False,
PlotRange -> {{-15, 17}, {-15, 15}, {0, 35}},
ViewPoint -> {0, -5, 0},
SphericalRegion -> True, ImageSize -> {500, 500}]], {{t, 1,
"times"}, 1, 14, 1},
{{opacity, 0.7}, 0.1, 1}, {{color, Blue}, ColorSlider}