那些你是否还记得的导数

1、最常出现同时也是最简单的导数公式为幂函数的求导。如右图，在求导时只用将幂移至前面，并将原先的幂减去一即可。

同时，这类求导也可能变为多个项相加或者相减的形式。不过万变不离其宗，只要牢记基本型，这类求导也就没什么可怕的了。

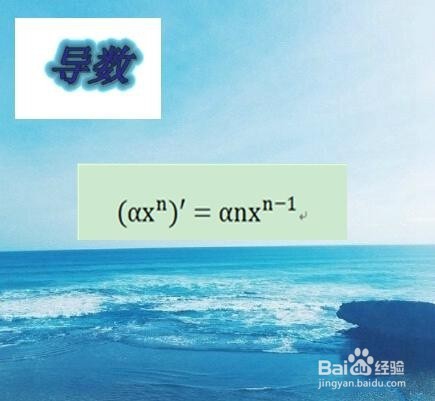
2、三角函数的求导。

这类求导一般会出现在含有三角函数运算的情况中。相比于幂函数的求导，三角函数的求导变幻在技巧性上略胜一筹（如右图）。不过只要在求导时弄清楚正负号也就万事大吉了。

3、在导数实际计算中，最容易碰到的要数指数函数和对数函数的求导。对于这类求导技巧并不高，只要记住基本公式即可。值得注意的是在这类求导中有两个特殊情况，即lnx和e^x的导数，记住这两种情况后，在解题中便能做到事半功倍。

4、在对基本初等函数的求导公式有了大致印象后，还需要趁热打铁就是导数的加减乘除法。特别应该注意的是导数的除法即分式的导数，在变幻过程中务必反复检验求导的符号。否则极有可能功亏一篑。

5、对于某些需要提升的同学来说，掌握最后一种类型的求导即复合函数的求导是极为必须和必要的。

求这类函数的导数时，我们不妨先分清内函数和外函数的概念。如右图，G（）为外函数，f(x)为内函数。在求导时，先求外函数的导数，也就是把f(x)当成一个自变量，一个整体求导。然后再将内函数求导。整个复合函数的导数就等于内外函数导数的乘积。这里变幻的不等式在右图中给出了一个简单的例子，供大家学习参考。