四边形的等角共轭点（网络画板演示）

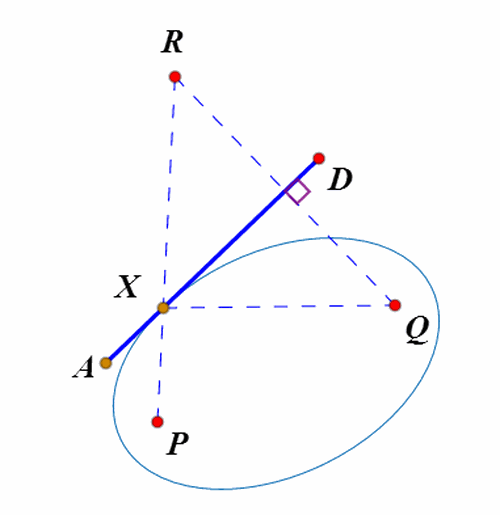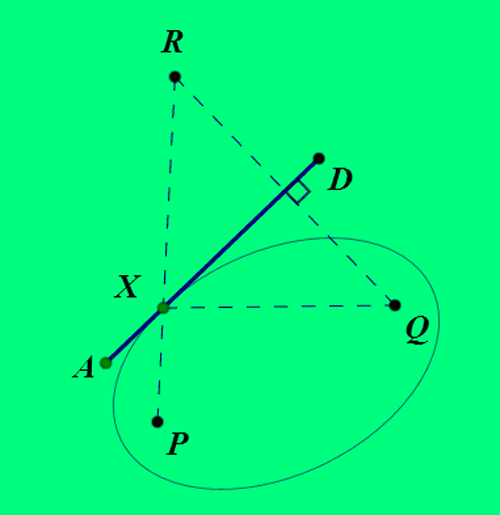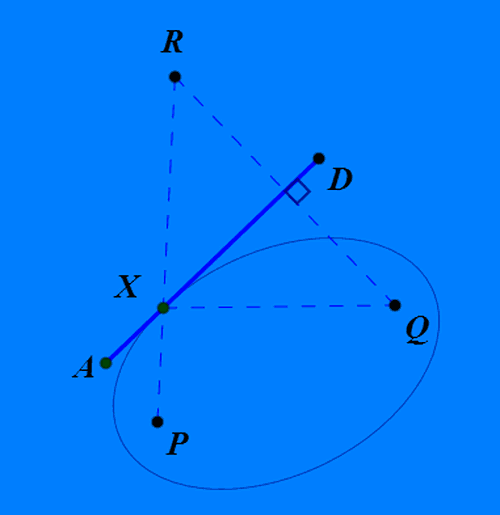
1、设一条直线AB与椭圆切于X，椭圆的焦点是P和Q，那么，直线AB是∠PXQ的外角平分线。

这个结论无需计算，稍微动动脑，就可以发现，这是显然的：

设Q关于AB的对称点是R；

观察发现，直线AB上，到P和Q的距离之和最小的点就是X；

所以，P、R、X三点共线；

所以，AB平分∠QXR。

2、如果椭圆外一点A到椭圆的两条切线分别是AX和AY，焦点是P和Q，那么，∠XAY和∠PAQ有相同的角平分线。

也就是∠YAP=∠XAQ。

3、如果椭圆外一点A到椭圆的两条切线分别是AX和AY，焦点是P和Q，那么，P和Q在AX和AY上的投影点共圆，圆心是PQ中点。

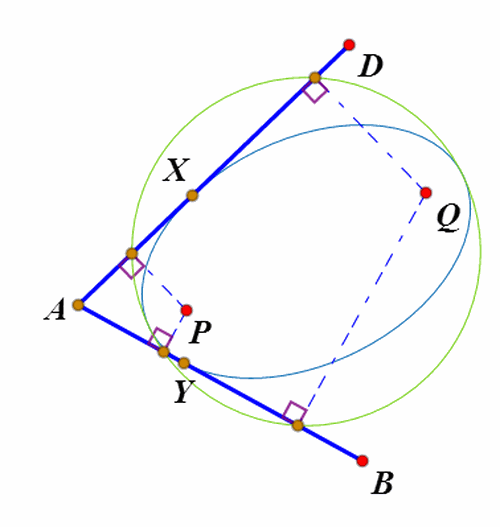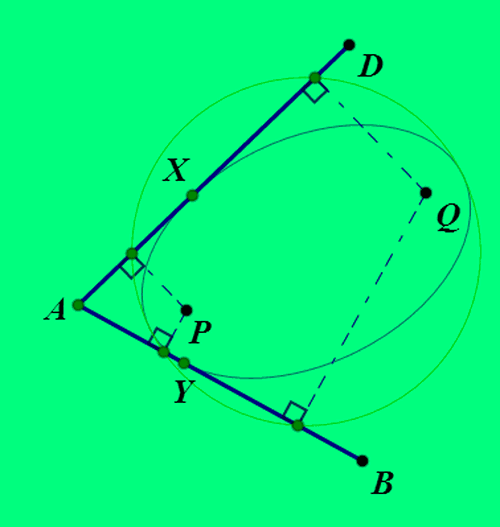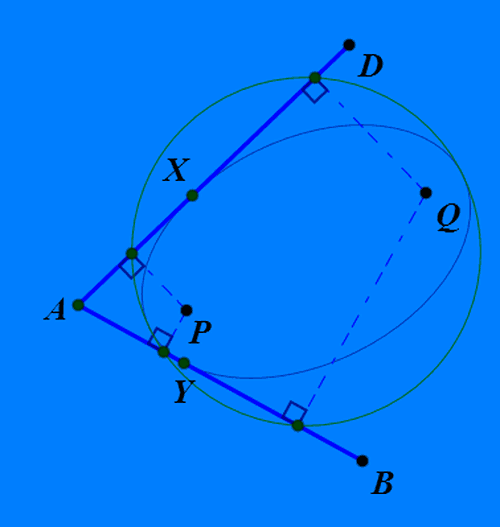
4、如果四边形ABCD的四条边都与椭圆相切，P和Q是切点，那么，P和Q在四边的投影点共圆，圆心是椭圆中心。

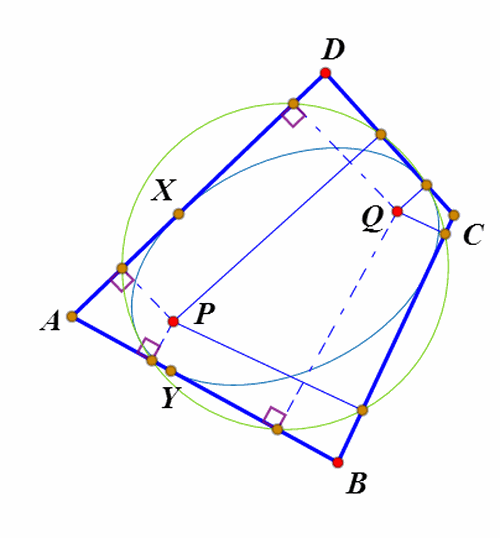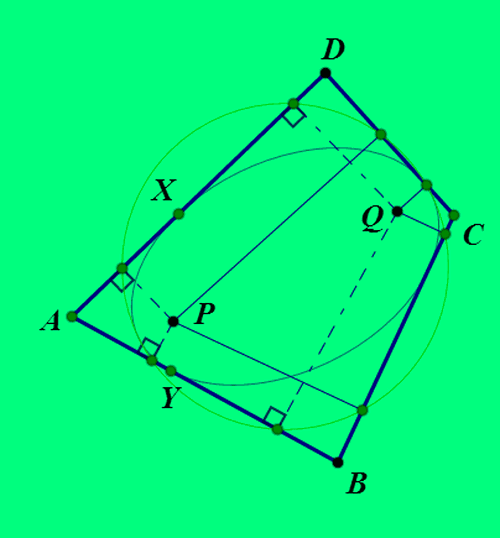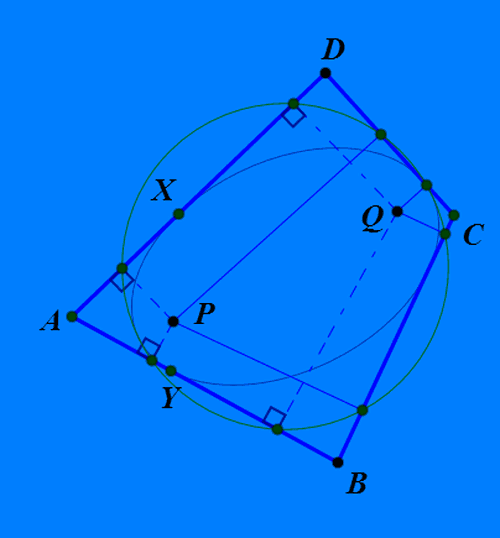
5、P和Q是关于四边形ABCD的等角共轭点。

6、如果椭圆是四边形的内切椭圆，那么，∠APB+∠CPD=180°。

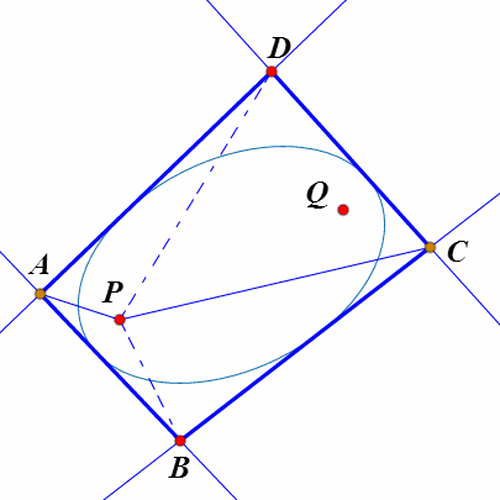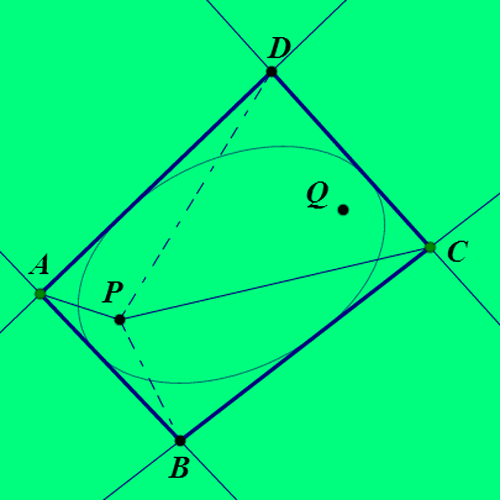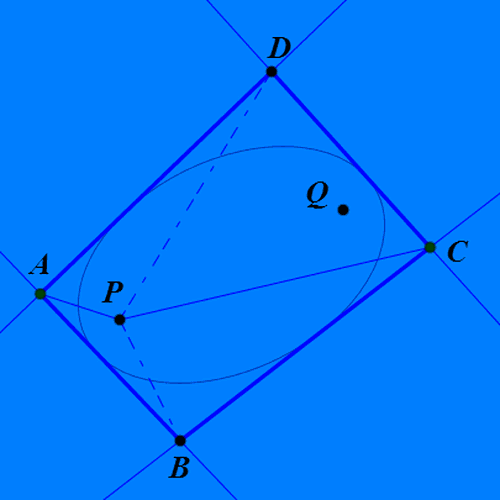
7、如果椭圆是四边形ABCD的旁切椭圆，那么，∠APB=∠CPD。

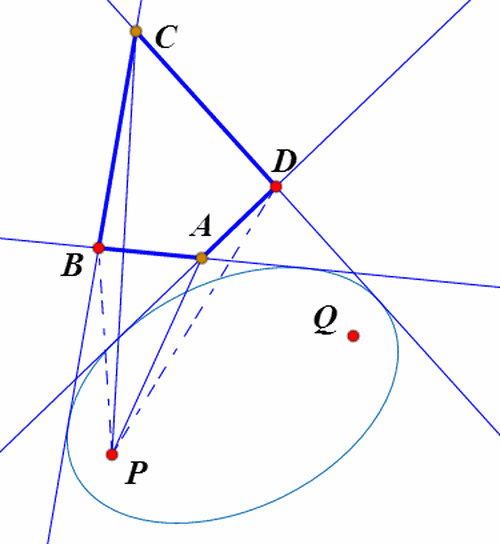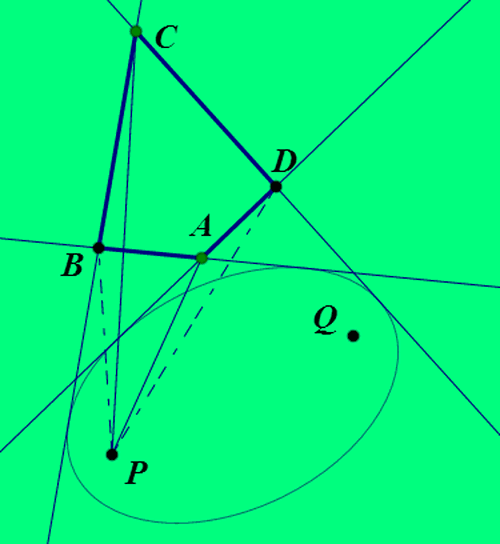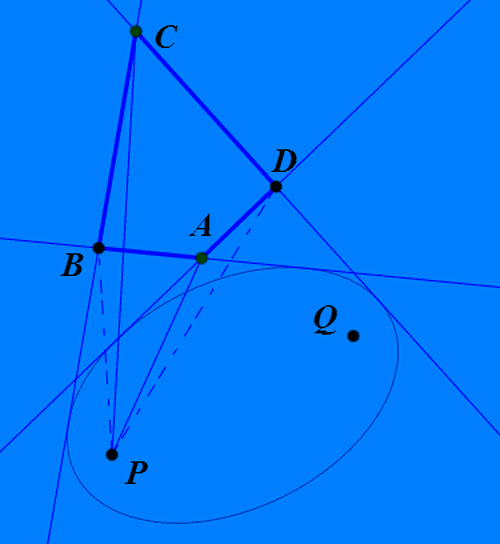
8、如果把整个图形放在复平面上，那么A、B、C、D、P、Q就对应六个复数；

又因为∠APB+∠CPD=180°或∠APB=∠CPD，所以：

(P-A)/(P-B)*(P-C)/(P-D)是实数，也就是虚部等于0。

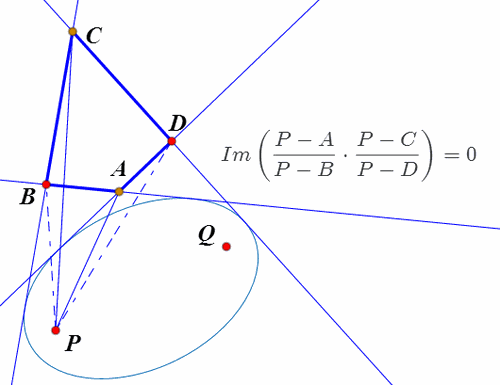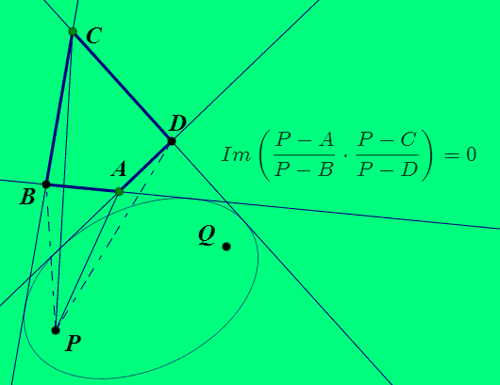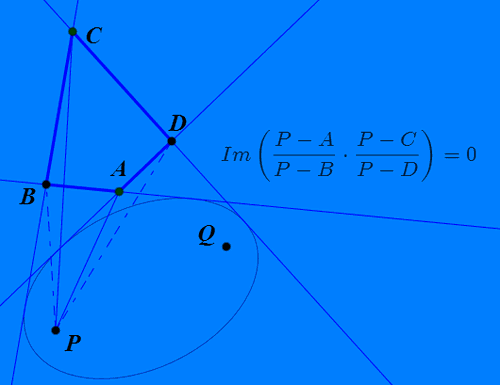
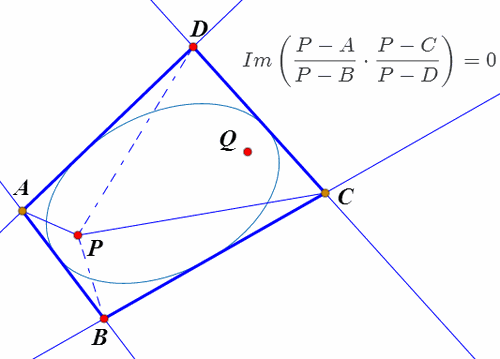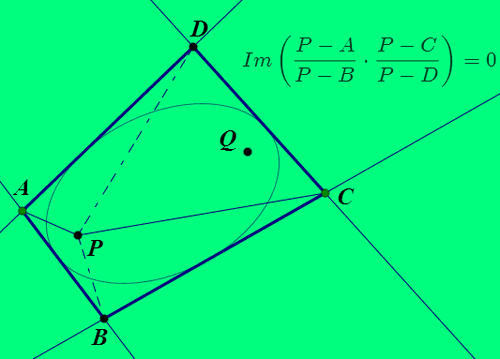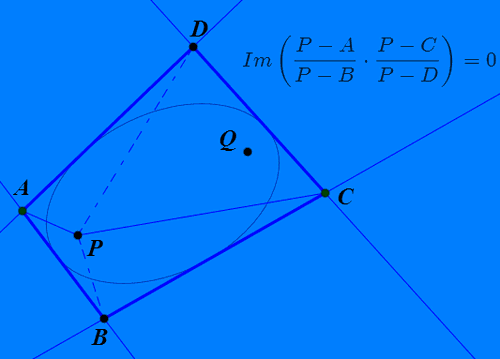
9、四边形ABCD所有的等角共轭点的轨迹，是图中的绿色曲线。

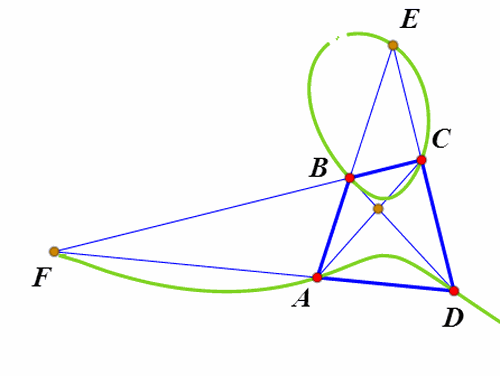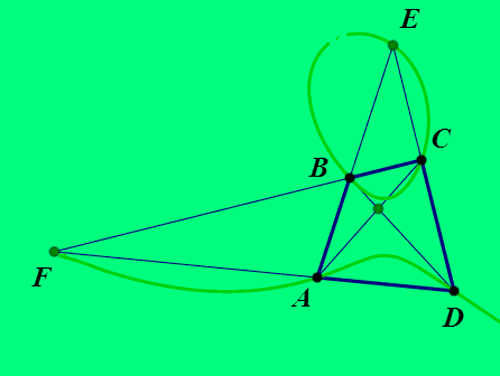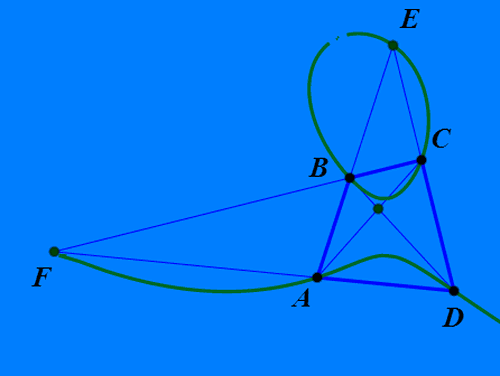
10、一个问题：

凸四边形ABCD的对角线的中点分别是E、F，

G是线段EF上的点（不包括端点E和F），

（1）、求证：ABCD内存在唯一的内切椭圆，以G为中心；

在不画出椭圆的前提下作图：

（2）、确定椭圆与四边形各边的切点；

（3）、确定这个椭圆焦点的位置。