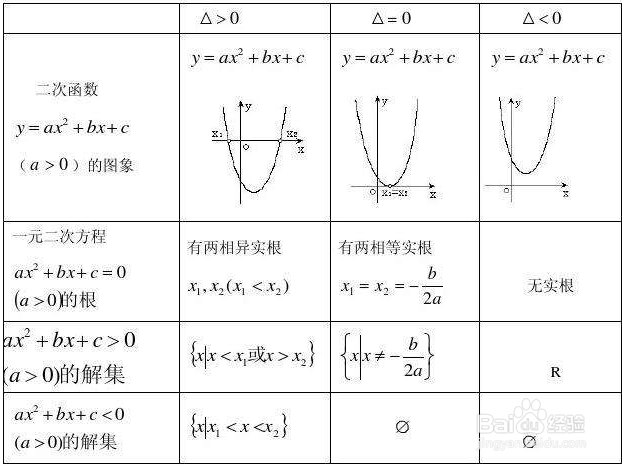
怎样求解一元二次方程（四种）

1、先判断△=b²-4ac，

若△<0原方程无实根；

2、若△=0，

原方程有两个相同的解为：

X=-b/（2a）；

3、若△>0，

原方程的解为：

X=（（-b）±√（△））/（2a）。

1、先把常数c移到方程右边得：

aX²+bX=-c

2、将二次项系数化为1得：

X²+（b/a）X=- c/a

3、方程两边分别加上（b/a）的一半的平方得：

X²+（b/a）X +（b/（2a））²=- c/a +（b/（2a））²

4、方程化为:

（b+（2a））²=- c/a +（b/（2a））²

5、①、若- c/a +（b/（2a））²<0，原方程无实根；

②、若- c/a +（b/（2a））² =0，原方程有两个相同的解为X=-b/（2a）；

③、若- c/a +（b/（2a））²>0，原方程的解为X=（-b）±√（（b²-4ac））/（2a）。

1、形如(X-m)²=n (n≥0)一元二次方程可以直接开平方法求得解为X=m±√n

1、将一元二次方程aX²+bX+c=0化为如（mX-n）（dX-e）=0的形式可以直接求得解为X=n/m，或X=e/d。