含1.5π+α诱导类型三角函数的不定积分

1、sin(3π/2+α)=-cosα

cos(3π/2+α)=sinα

tan(3π/2+α)=-cotα

cot(3π/2+α)=-tanα

sec(3π/2+α)=-cscα

csc(3π/2+α)=secα

2、图例解析如下：

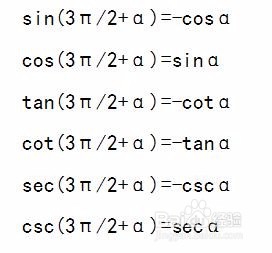
1、∫sin(3π/2+α)dα

=∫sin(3π/2+α)d(3π/2+α)

=-cos(3π/2+α)+c

=cos(π/2+α)+c

=-sinα+c

2、图例解析如下：

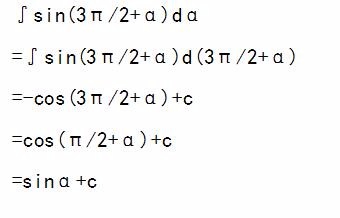
1、∫cos(3π/2+α)dα

=∫cos(3π/2+α)d(3π/2+α)

=sin(3π/2+α)+c

=-sin(π/2+α)+c

=-cosα+c

2、图例解析如下：

1、∫tan(3π/2+α)dα

=∫[sin(3π/2+α) d(3π/2+α)/ cos(3π/2+α)]

=-∫d cos(3π/2+α)/cos(3π/2+α)

=-ln|cos(3π/2+α)|+c

=-ln|sinα|+c

2、图例解析如下：

1、 

∫cot(3π/2+α)dα

=∫[cos(3π/2+α) d(3π/2+α)/ sin(3π/2+α)]

=∫d sin(3π/2+α)/sin(3π/2+α)

=ln|sin(3π/2+α)|+c

=ln|cosα|+c

2、图例解析如下：

1、∫sec(3π/2+α)dα

=∫d(3π/2+α)/ cos(3π/2+α)

=∫cos(3π/2+α)d(3π/2+α)/ [cos(3π/2+α)]^2

=∫dsin(3π/2+α)/ {1-[sin(3π/2+α)]^2}

=∫dsin(3π/2+α)/ {[1-sin(3π/2+α)][1+ sin(3π/2+α)]}

=(1/2){∫dsin(3π/2+α)/ [1-sin(3π/2+α)]+∫dsin(3π/2+α)/ [1+sin(3π/2+α)]}

=(1/2)ln{[1+sin(3π/2+α)]/ [1-sin(3π/2+α)]}+c

=(1/2)ln[(1+cosα)/(1-cosα)]+c

=(1/2)ln[(1+cosα)^2/(sinα)^2]+c

=ln|(1+cosα)/sinα|+c

=ln|cscα+cotα|+c

2、图例解析如下：

1、∫csc(3π/2+α)dα

=∫d(3π/2+α)/ sin(3π/2+α)

=∫sin(3π/2+α)d(3π/2+α)/ [sin(3π/2+α)]^2

=-∫dcos(3π/2+α)/ {1-[cos(3π/2+α)]^2}

=-∫dcos(3π/2+α)/ {[1-cos(3π/2+α)][1+ cos(3π/2+α)]}

=-(1/2){∫dcos(3π/2+α)/ [1-cos(3π/2+α)]+∫dcos(3π/2+α)/ [1+cos(3π/2+α)]}

=-(1/2)ln{[1+cos(3π/2+α)]/ [1-cos(3π/2+α)]}+c

=-(1/2)ln[(1-sinα)/(1+sinα)]+c

=-(1/2)ln[(1-sinα)^2/(cosα)^2]+c

=-ln|(1-sinα)/cosα|+c

=-ln|secα-tana|+c

2、图例解析如下：