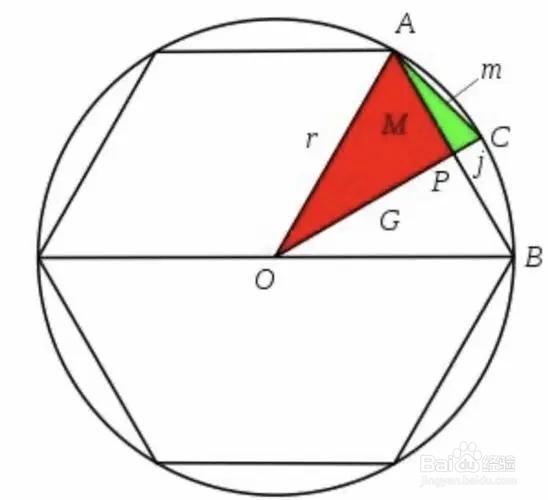
割圆术求出圆周率方法

1、将圆分割成多边形，分割来越细，多边形的边数越多，多边形的面积就和圆面积没有差别了。他说，将6边形一边的长度乘以圆半径，再乘3，得12边形的面积。将12边形的一边长乘半径，再乘6，得24边形面积。越割越细，多边形和圆面积的差越小。如此割了再割，最后终于和圆合为一体，毫无差别了。6边形的面积显然和圆面积相差很多。内接正12边形面积 = 6边形面积+6个蓝色三角形面积，向圆面积趋近了一步。

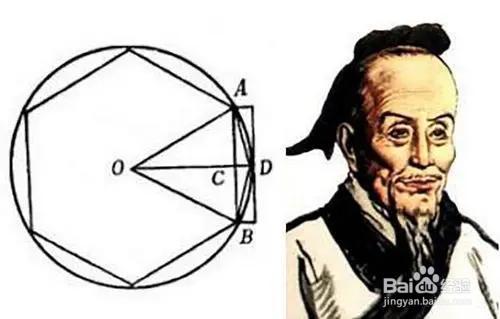
2、正24边形面积=6边形面积+6个蓝色三角形面积+12个黄色三角形面积，更加接近圆面积了。显然：正12边形面积 <正24边形面积< 正48边形面积<稆糨孝汶;正96边形面积……<内接6*2N边形面积<圆面积。内接 6*2N边形面积圆面积。他又指出：6边形之外，遗留了半径的一小段d ，称为余径。将余径d乘多边形的一边，所得长方形ABCD，已经越出圆周范围之外。如果将圆周分割得很细，余径d趋向于0，而长方形ABCD的面积也趋向于0。显然，刘徽之所以研究余径，目的是从上限和下限两个方面逐步逼近圆面积：内接 6*2N边形面积圆面积内接 6*2N边形面积+6*2N*d*L。

3、刘徽进一步证明圆面积=圆周/2 × 半径。关于多边形的面积，刘徽有如下公式：2 N边形的面积= N边形的半周长×R。=,其中L为N边形的单边长，R为圆半径。此公式可用刘徽出入相补原理证明： 将内接2N边形，分割，然后重新排列成宽为 L x N/2, 高为R的长方形；显然2N边形的面积=长方形面积==N边形的半周长 * R

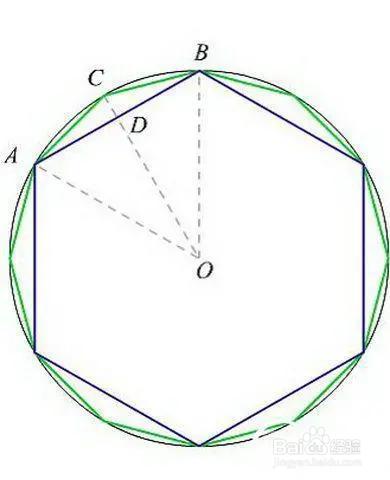
4、当N边形的半周长圆的半周长2N边形面积=N边形的半周长 * R圆面积所以圆的半周长 * R = 圆面积因此圆周 = 2* 圆面积/R圆周率圆周/直径= 2* 圆面积/(R*2R)= 圆面积/R2=2N边形的面积/R2