C#用迪杰斯特拉算法(Dijkst)求最短路径
1、我要做这个算法,首先要理解迪杰斯特拉算法。然后能画图程序执行流程图,这里我就做了个简单的流程图
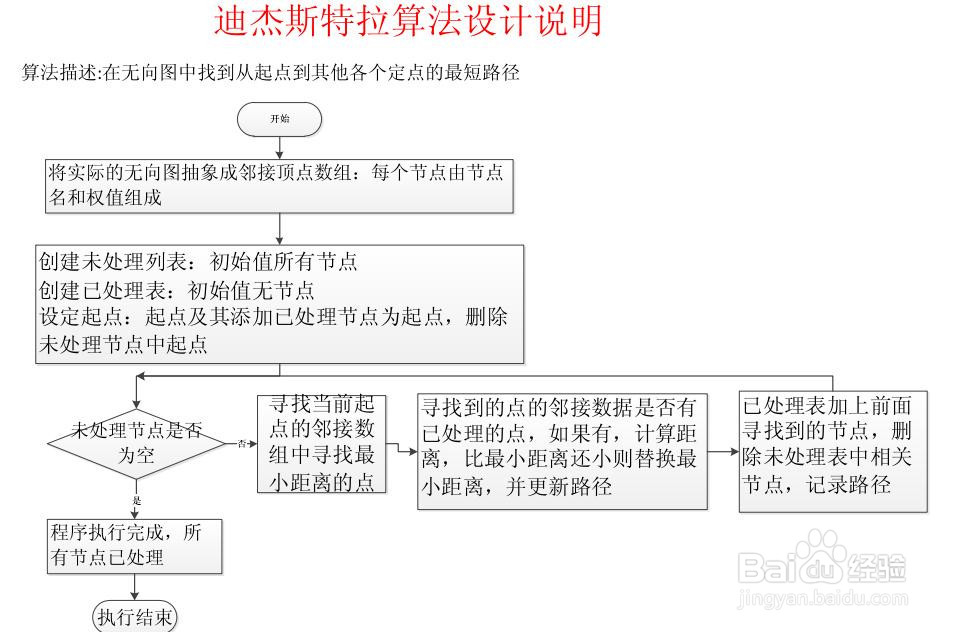
2、创建一个Windows窗体程序,程序界面如下。
pictureBox1控件显示算法用到的基础数据图片;
comboBox1设置算法的起点,默认"A";
算法检验按钮(btn_JY),执行算法。

3、首先创建一个类“Dijskst_shixian.cs”,用来设计迪杰斯特拉算法的实现。
4、在类Dijskst_shixian.cs中定义了一个结构Node,这个节点记录点和权值。
public struct Node
{
public string Node_Name;
public int Node_QuanZhi;
}
5、创建一个泛型对象:public List<List<Node>> node_List = new List<List<Node>>(); 记录节点和权值。
用create()方法创建图的邻接点
public void Create() {
node_List = new List<List<Node>>();
List<Node> nn = new List<Node>();
nn = new List<Node>();
Node node = new Node();
node.Node_QuanZhi = 0;
node.Node_Name = "A";
nn.Add(node);
Node node1 = new Node();
node1.Node_QuanZhi = 6;
node1.Node_Name = "B";
nn.Add(node1);
Node node2 = new Node();
node2.Node_QuanZhi = 3;
node2.Node_Name = "C";
nn.Add(node2);
node_List.Add(nn);
nn = new List<Node>();
Node N = new Node();
N.Node_Name = "B";
N.Node_QuanZhi = 0;
nn.Add(N);
Node N1 = new Node();
N1.Node_Name = "A";
N1.Node_QuanZhi = 6;
nn.Add(N1);
Node N2 = new Node();
N2.Node_Name = "C";
N2.Node_QuanZhi = 2;
nn.Add(N2);
Node N3 = new Node();
N3.Node_Name = "D";
N3.Node_QuanZhi = 5;
nn.Add(N3);
node_List.Add(nn);
nn = new List<Node>();
Node NN = new Node();
NN.Node_Name = "C";
NN.Node_QuanZhi = 0;
nn.Add(NN);
Node NN1 = new Node();
NN1.Node_Name = "A";
NN1.Node_QuanZhi = 3;
nn.Add(NN1);
Node NN2= new Node();
NN2.Node_Name = "B";
NN2.Node_QuanZhi = 2;
nn.Add(NN2);
Node NN3 = new Node();
NN3.Node_Name = "D";
NN3.Node_QuanZhi = 3;
nn.Add(NN3);
Node NN4 = new Node();
NN4.Node_Name = "E";
NN4.Node_QuanZhi = 4;
nn.Add(NN4);
node_List.Add(nn);
nn = new List<Node>();
Node NNN = new Node();
NNN.Node_Name = "D";
NNN.Node_QuanZhi = 0;
nn.Add(NNN);
Node NNN1 = new Node();
NNN1.Node_Name = "B";
NNN1.Node_QuanZhi = 5;
nn.Add(NNN1);
Node NNN2 = new Node();
NNN2.Node_Name = "C";
NNN2.Node_QuanZhi = 3;
nn.Add(NNN2);
Node NNN3 = new Node();
NNN3.Node_Name = "E";
NNN3.Node_QuanZhi = 2;
nn.Add(NNN3);
Node NNN4 = new Node();
NNN4.Node_Name = "F";
NNN4.Node_QuanZhi = 4;
nn.Add(NNN4);
node_List.Add(nn);
nn = new List<Node>();
Node NNNN = new Node();
NNNN.Node_Name = "E";
NNNN.Node_QuanZhi = 0;
nn.Add(NNNN);
Node NNNN1 = new Node();
NNNN1.Node_Name = "D";
NNNN1.Node_QuanZhi = 2;
nn.Add(NNNN1);
Node NNNN2 = new Node();
NNNN2.Node_Name = "C";
NNNN2.Node_QuanZhi = 4;
nn.Add(NNNN2);
Node NNNN3 = new Node();
NNNN3.Node_Name = "F";
NNNN3.Node_QuanZhi = 5;
nn.Add(NNNN3);
node_List.Add(nn);
nn = new List<Node>();
Node NNNNN = new Node();
NNNNN.Node_Name = "F";
NNNNN.Node_QuanZhi = 0;
nn.Add(NNNNN);
Node NNNNN1 = new Node();
NNNNN1.Node_Name = "D";
NNNNN1.Node_QuanZhi = 3;
nn.Add(NNNNN1);
Node NNNNN2 = new Node();
NNNNN2.Node_Name = "E";
NNNNN2.Node_QuanZhi = 5;
nn.Add(NNNNN2);
node_List.Add(nn);
nn = new List<Node>();
Node NNNNNN = new Node();
NNNNNN.Node_Name = "G";
NNNNNN.Node_QuanZhi = 0;
nn.Add(NNNNNN);
Node NNNNNN1 = new Node();
NNNNNN1.Node_Name = "D";
NNNNNN1.Node_QuanZhi = 2;
nn.Add(NNNNNN1);
Node NNNNNN2 = new Node();
NNNNNN2.Node_Name = "F";
NNNNNN2.Node_QuanZhi = 3;
nn.Add(NNNNNN2);
node_List.Add(nn);
}
6、核心算法:
List<string> WeiChuLiDingDian = new List<string>();
List<string> ChuLiDian = new List<string>();
public List<Node> LJ = new List<Node>();
public List<string> LJ_Path = new List<string>();
public void SuanFa(Node dingdian,List<List<Node>> ListListNode) {
WeiChuLiDingDian.Clear();
for (int I = 0; I < ListListNode.Count;I++ )
WeiChuLiDingDian.Add(ListListNode[I][0].Node_Name); ChuLiDian.Clear();
LJ.Clear();
LJ_Path.Clear();
LJ_Path.Add(dingdian.Node_Name+"->"+dingdian.Node_Name); dingdian.Node_QuanZhi = 0;
LJ.Add(dingdian);
ChuLiDian.Add(dingdian.Node_Name);
WeiChuLiDingDian.Remove(dingdian.Node_Name);
int ChangDu = ListListNode.Count;
for (int i = 0; i < ChangDu; i++)
{
for (int dd = 0; dd < ChangDu; dd++)
{
if (ListListNode[dd][0].Node_Name == dingdian.Node_Name) {
//第一步:从邻接图顶点中找到最小距离
// int min = dingdian.Node_QuanZhi + node_List[dd][1].Node_QuanZhi;
int min = 10000;
Node xunzhao_node=new Node();
xunzhao_node.Node_Name = "";
string path = "";
// xunzhao_node.Node_Name = ListListNode[dd][1].Node_Name;
for (int ljd = 1; ljd < ListListNode[dd].Count; ljd++) {
if (WeiChuLiDingDian.Contains(ListListNode[dd][ljd].Node_Name)) {
if (dingdian.Node_QuanZhi + ListListNode[dd][ljd].Node_QuanZhi < min)
{
min = dingdian.Node_QuanZhi + ListListNode[dd][ljd].Node_QuanZhi;
xunzhao_node.Node_QuanZhi = min; xunzhao_node.Node_Name = ListListNode[dd][ljd].Node_Name;
path = LJ_Path[LJ_Path.Count - 1] + "->" + xunzhao_node.Node_Name;
}
}
}
if (xunzhao_node.Node_Name == "")
{
if(WeiChuLiDingDian.Count>0)
xunzhao_node.Node_Name = WeiChuLiDingDian[0]; path = xunzhao_node.Node_Name;
} //寻找到了从顶点到邻接点最小距离,之后再从找到的点寻找邻接点
for (int xunzhaodaodian = 0; xunzhaodaodian < ChangDu; xunzhaodaodian++)
{
if (ListListNode[xunzhaodaodian][0].Node_Name == xunzhao_node.Node_Name)
{
for (int xzd_ljd = 1; xzd_ljd < ListListNode[xunzhaodaodian].Count; xzd_ljd++)
{
for(int lj=0;lj<LJ.Count;lj++)
if (ListListNode[xunzhaodaodian][xzd_ljd].Node_Name == LJ[lj].Node_Name)
{
int minmin=LJ[lj].Node_QuanZhi+ ListListNode[xunzhaodaodian][xzd_ljd].Node_QuanZhi;
if (min > minmin) {
min = minmin; xunzhao_node.Node_QuanZhi = minmin; path = LJ_Path[lj] + "->" + xunzhao_node.Node_Name; }
}
}
}
} //查找成功
dingdian = xunzhao_node;
LJ.Add(dingdian);
ChuLiDian.Add(dingdian.Node_Name);
WeiChuLiDingDian.Remove(dingdian.Node_Name); LJ_Path.Add(path);
continue;
}
}
}
}
7、算法检验设计代码:
创建一个对象:Dijskst_shixian dijs = new Dijskst_shixian();
默认节点"A":
if (comboBox1.Text != "")
node.Node_Name = comboBox1.Text;
else
node.Node_Name = "A";
执行创建和算法函数
dijs.Create();dijs.SuanFa(node,dijs.node_List);
显示输出信息:
for (int i = 0; i < dijs.LJ.Count-1; i++)
{
richTextBox1.AppendText("起点"+node.Node_Name+"到顶点:"+dijs.LJ[i].Node_Name + " ;最短路径: " + dijs.LJ[i].Node_QuanZhi+" ; 路径: "+dijs.LJ_Path[i]+" ;\r\n");
}

8、运行编译程序,执行“算法检验”,默认“A”为起点,计算A到其他点的最短路径,执行结果在红框中。
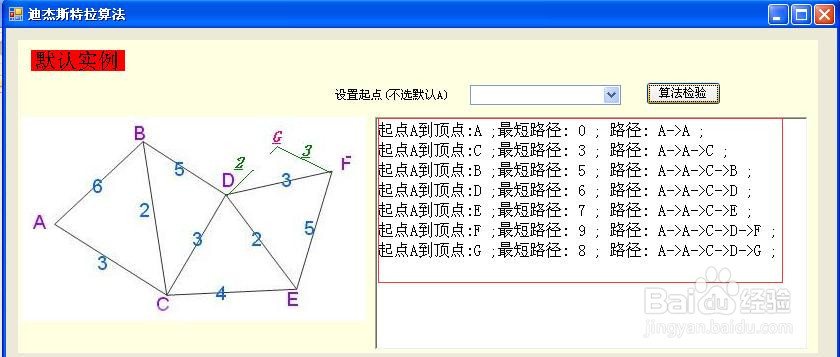
9、运行编译程序,执行“算法检验”,选择以“C”为起点,计算C到其他点的最短路径,执行结果在红框中。
