蒙特卡洛模拟

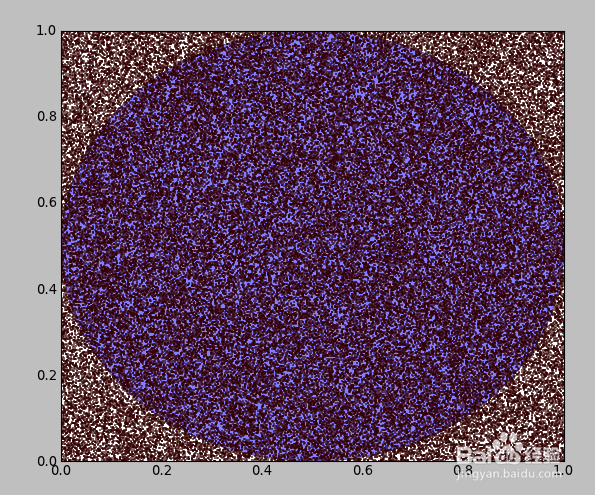
1、求解圆周率π，在平面中随机抽样，分布着一定数量的点，点的分布服从均匀分布。通过求解点落在圆内的概率，即可求解圆的面积与平面面积的比值，而求解出圆周率π。

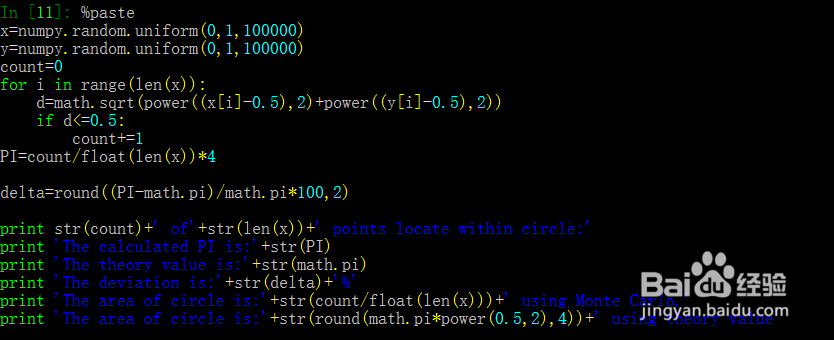
2、代码演示及结果x=numpy.random.uniform(0,1,100000)y=numpy.random.uniform(0,1,100000)count=0for i in range(len(x)): d=math.sqrt(power((x[i]-0.5),2)+power((y[i]-0.5),2)) if d<=0.5: count+=1PI=count/float(len(x))*4delta=round((PI-math.pi)/math.pi*100,2)print str(count)+' of'+str(len(x))+' points locate within circle:'print 'The calculated PI is:'+str(PI)print 'The theory value is:'+str(math.pi)print 'The deviation is:'+str(delta)+'%'print 'The area of circle is:'+str(count/float(len(x)))+' using Monte Carlo.'print 'The area of circle is:'+str(round(math.pi*power(0.5,2),4))+' using theory value'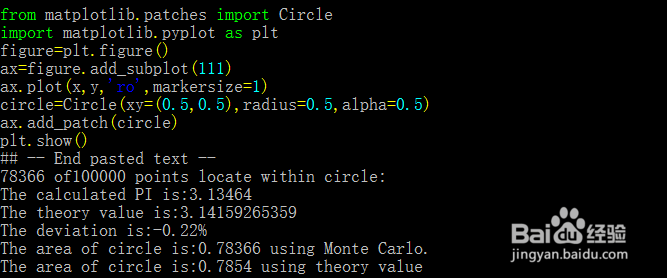from matplotlib.patches import Circleimport matplotlib.pyplot as pltfigure=plt.figure()ax=figure.add_subplot(111)ax.plot(x,y,'ro',markersize=1)circle=Circle(xy=(0.5,0.5),radius=0.5,alpha=0.5)ax.add_patch(circle)plt.show()

3、数值积分。对复杂函数的积分，可以使用此方法，误差是存在的。但是方便快捷。与第一个例子类似，也是抽样分析。分析点落在积分面积的概率。

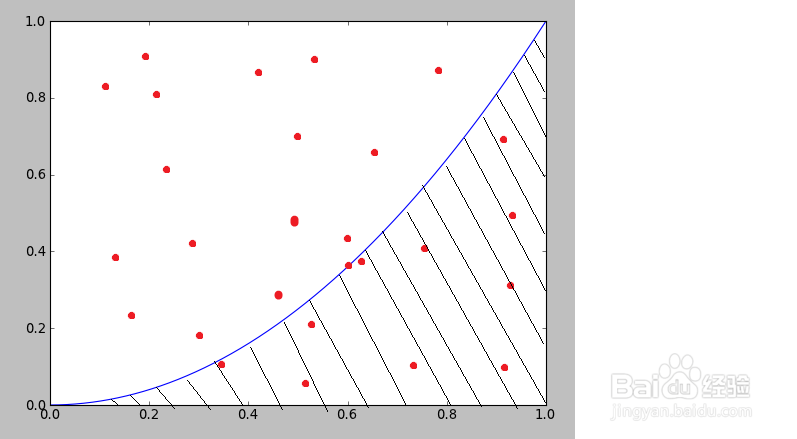
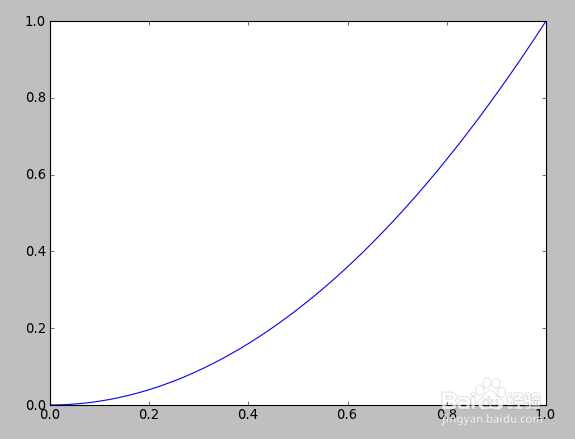
4、代码演示及结果a=numpy.linspace(0,1,10000)b=power(a,2)figure=plt.figure()ax=figure.add_subplot(111)ax.plot(a,b,'b-')plt.show()f=lambda x:power(x,2)x=numpy.random.uniform(0,1,1000000)y=numpy.random.uniform(0,1,1000000)count=0for i in range(len(x)): if y[i]<=f(x[i]): count+=1print count/float(len(x))print 1/float(3)

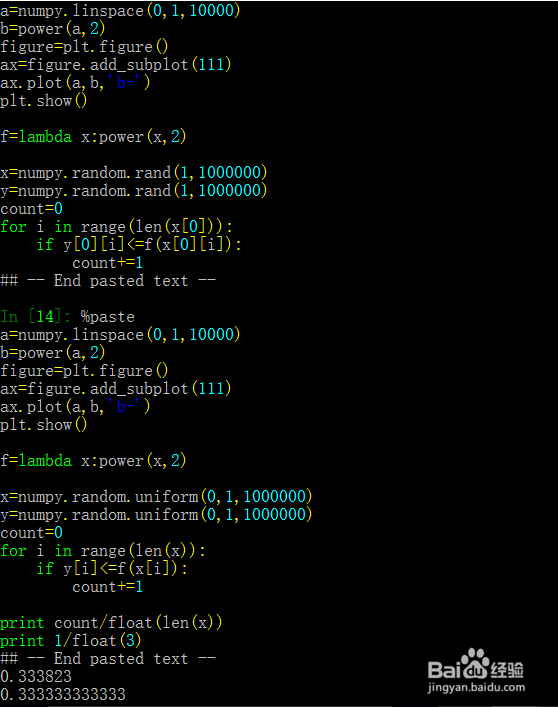
5、人口问题模拟例如某些人生二胎是为了，生男孩，那么采用这种策略会影响男女性别比例吗？

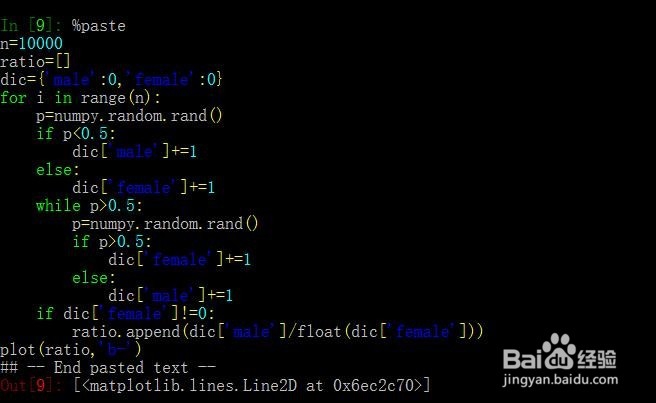
6、代码如下：n=10000ratio=[]dic={'male&#补朱锚卦39;:0,'femal髫潋啜缅e':0}for i in range(n): p=numpy.random.rand() if p<0.5: dic['male']+=1 else: dic['female']+=1 while p>0.5: p=numpy.random.rand() if p>0.5: dic['female']+=1 else: dic['male']+=1 if dic['female']!=0: ratio.append(dic['male']/float(dic['female']))plot(ratio,'b-')通过模拟我们发现其实不会影响。男女比例大致为1:1