等内切圆的部分问题集锦
本文,我要给大家介绍一些网上流传已久的几个关于等内切圆的问题。 前面写了一篇经验,里面提到了某个博客,结果被认定为“替他人做宣传”。真是滑稽!
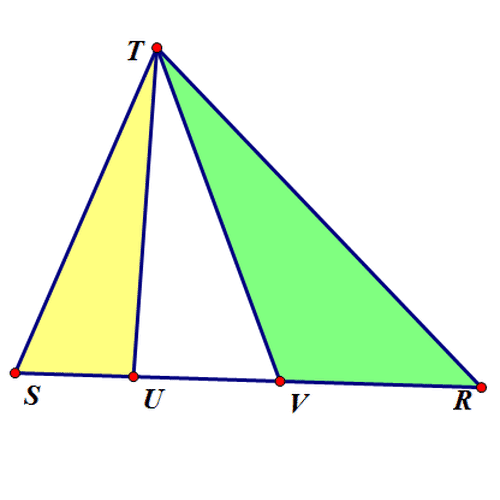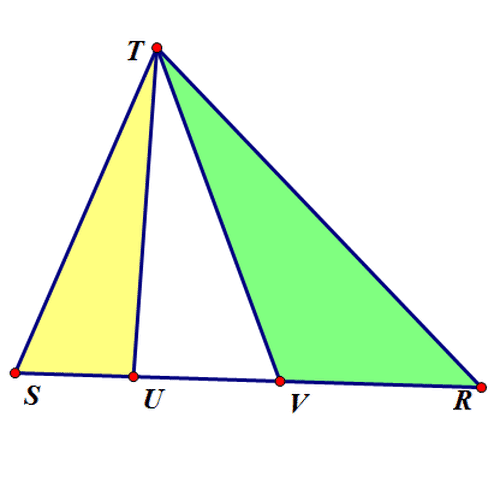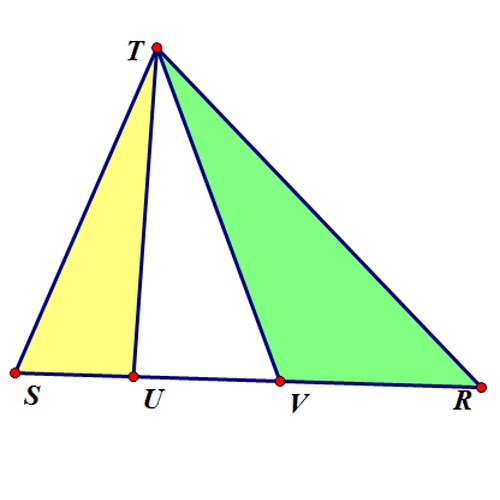
2、 第二个问题: 设△ABW和△AWC的内切圆半径相等,求洵翌绦枞证:4(AW^2)=((AB+AC)^2)-(BC^2)。 证骈跪爸锂明过程如下: 设AB=c,AC=b,BC=a,BW=x,CW=y; ∵ △ABW和△AWC的内切圆半径相等, ∴ (S△ABW/S△AWC)=(L△ABW/L△AWC),即(x/y)=(h+c+x/h+b+y)=(h+c/h+b); ∵ x+y=a,∴ x=(ac+ah/b+c+2h),y=(ab+ah/b+c+2h); 根据海伦公式,有: S△ABW=(x/x+y)S△ABC =(h+c/2h+b+c)S△ABC=(h+c/2h+b+c)·(√((c+b+a)(c+b-a)(c-b+a)(-c+b+a))/4)=(h+c/2h+b+c)·(√((c^4)+(b^4)+(a^4)-2(c^2)(a^2)-2(b^2)(c^2)-2(a^2)(b^2))/4), 另外,有: S△ABW=(√((c+h+x)(c+h-x)(c-h+x)(-c+h+x))/4)=(√((c^4)+(h^4)+(x^4)-2(c^2)(x^2)-2(h^2)(c^2)-2(x^2)(h^2))/4), ∴ (h+c/2h+b+c)·(√((c^4)+(b^4)+(a^4)-2(c^2)(a^2)-2(b^2)(c^2)-2(a^2)(b^2))/4)=(√((c^4)+(h^4)+(x^4)-2(c^2)(x^2)-2(h^2)(c^2)-2(x^2)(h^2))/4); 把 x=(ac+ah/b+c+2h)代入,化简得:h=√((((b+c)^2)-(a^2)/2))。
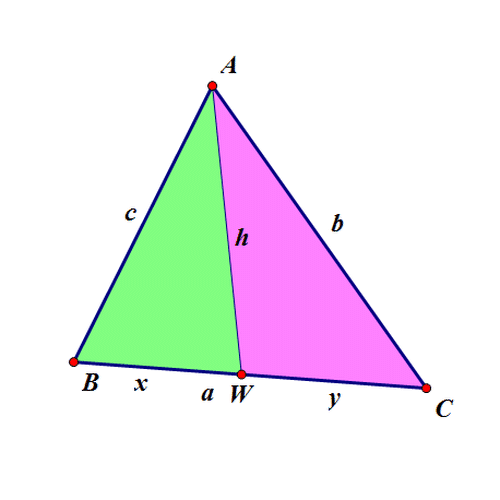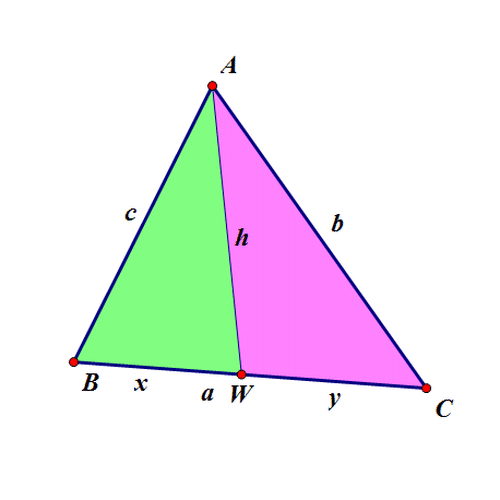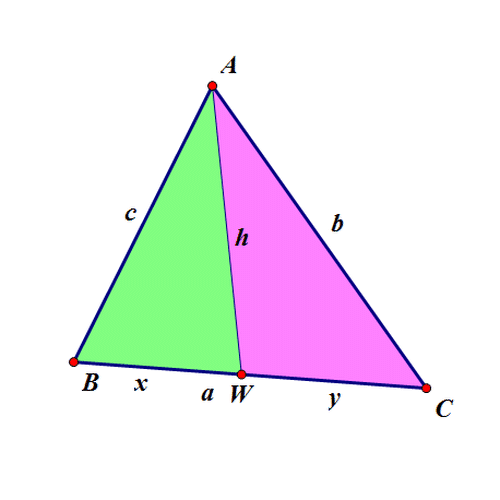

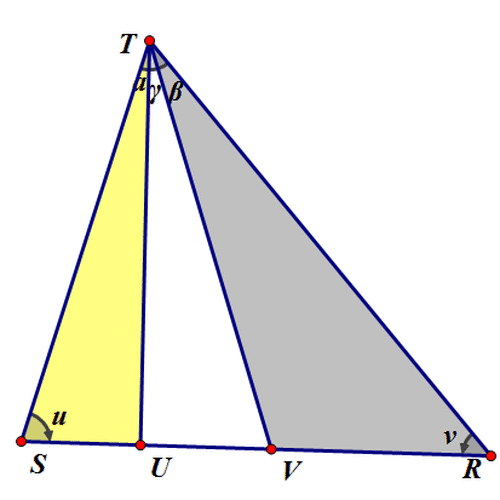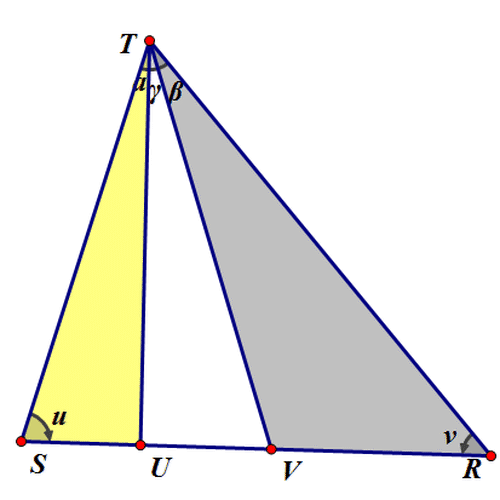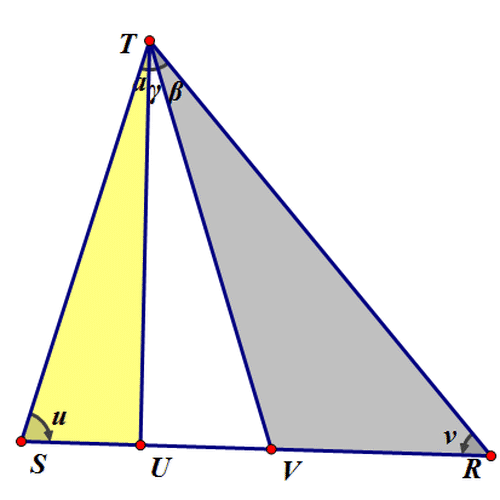


2、 给定△UVW,设各顶点坐标是:U = {0, 0}; V = {0, 1}; W = {1, 1}; 它的边长是:{u, v, w} = {Norm[V - W], Norm[W - U], Norm[U - V]}; 它的面积为: S[U_, V_, W_] := Sqrt[(u + v + w) (u + v - w) (u - v + w) (-u + v + w)]=(Sqrt((Norm[V - W] + Norm[W - U] + Norm[U - V]) (Norm[V - W] + Norm[W - U] - Norm[U - V]) (Norm[V - W] - Norm[W - U] + Norm[U - V]) (-Norm[V - W] + Norm[W - U] + Norm[U - V])))/4; 它的周长为: L[U_, V_, W_] := u + v + w= Norm[V - W] + Norm[W - U] + Norm[U - V]; 它的内切圆半径为: r[U_, V_, W_] := S[U, V, W]/L[U, V, W]; 如果X使得△XUV和△XUW的内切圆半径相等,那么X应该满足什么条件? 当然是:r[U, V, X] == r[U, X, W](假设这条曲线为Ω), 即 S[U, V, X]/L[U, V, X] == S[U, X, W]/ L[U, X, W], 进而化成:S[U, V, X] L[U, X, W] == L[U, V, X] S[U, X, W]; 同样地,如果X使得△XUV和△XVW的内切圆半径相等,那么X应该满足:S[U, V, X] L[V, X, W] == L[U, V, X] S[V, X, W](假设这条曲线为Ψ)。 Ω和Ψ的交点,就是所求的点。Mathematica代码如下:

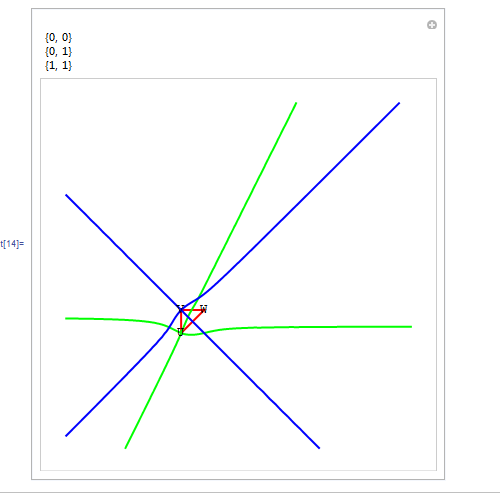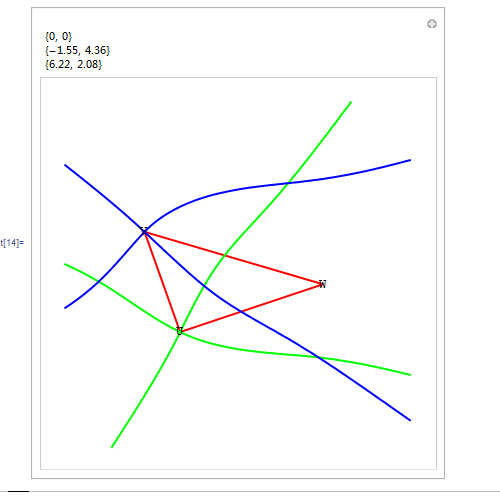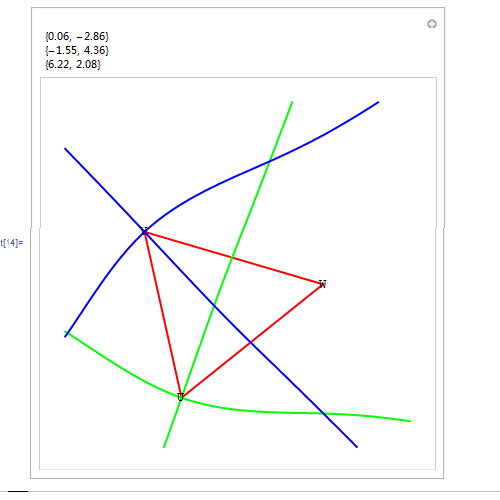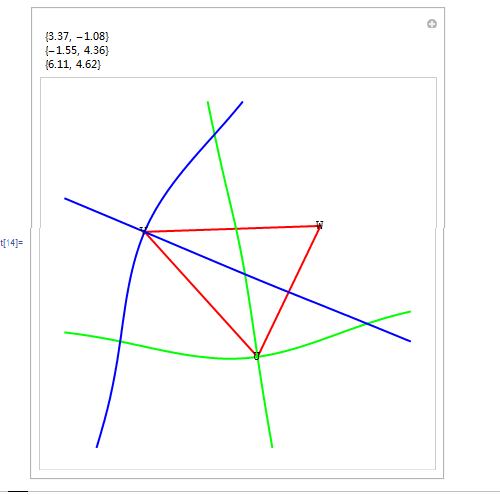
3、 把曲线Ω画成绿色的,把曲线Ψ画成蓝色的,并适当改变一下画图范围。具体的Mathematica代码如图:
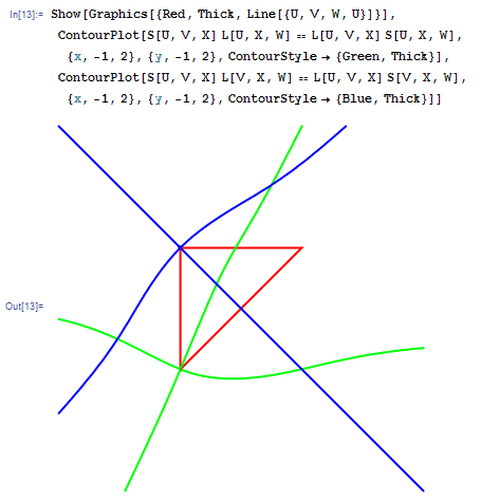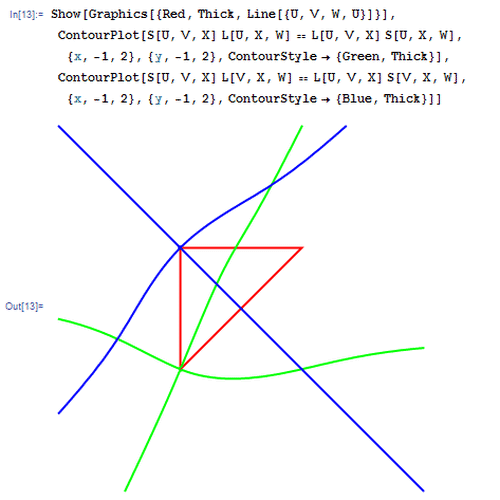
4、 上面的代码有个缺点,每次只能作出一个图,要想画出别的结果,必须重新定义U、V、W三点的坐标,显得很麻烦! 所以,有必要引进定位器来作图。关于定位器的用法,请移驾——《用Mathematica处理几何问题——定位器Locator》。 同样使用上面的自定义函数,并运行下图里的代码。特点是:可以用鼠标拖动△UVW的顶点,其坐标实时显示在左上角。 我曾尝试用Mathematica计算出Ω和Ψ的交点的坐标,但是失败了,就连粗略的数值坐标都算不出来!Solve[S[U, V, X] L[U, X, W] == L[U, V, X] S[U, X, W] && S[U, V, X] L[V, X, W] == L[U, V, X] S[V, X, W], {x, y}] 和NSolve[S[U, V, X] L[U, X, W] == L[U, V, X] S[U, X, W] && S[U, V, X] L[V, X, W] == L[U, V, X] S[V, X, W], {x, y}]。
