考研数学—数列的极限部分—常考题型与解题经验
1、极限的唯一性
2、收敛数列的有界性
3、收敛数列的保号性
4、收敛数列与其子数列的关系
1、常考题型1:用极限定义证明数列的极限
解答好本类题目的经验:
1.正确理解极限的e>0的任意给定性。
2.理解N的存在依赖于e。但并不唯一。
3.N一般不计其大小
本题型的例子:(解答中需要注意的地方用红笔标出)
解答这类题的步骤与经验总结:


2、常考题型2:放缩法在数列极限证明中的用法
解答好本类题目的经验:
1.不等式的放缩要适当。
2.对n值进行限定,可以简化解题过程。
本题型的例子:(解答中需要注意的地方用红笔标出)
解答这类题的步骤与经验总结:


3、常考题型3:用e~N法证明数列的极限
解答好本类题目的经验:
1.理解数列极限e~N的d定义。
2.|xn-a|<=e含义与|xn-a|<e等价
本题型的例子:(解答中需要注意的地方用红笔标出)
解答这类题的步骤与经验总结:


4、常考题型4:证明数列没有极限
解答好本类题目的经验:
1.改变或者增删xn的有限项,不影响数列的收敛性。
2.数列xn收敛的充要条件,是xn的任意一个子数列都收敛,且有相同极限。
本题型的例子:(解答中需要注意的地方用红笔标出)
解答这类题的步骤与经验总结:


5、常考题型5:证明数列发散
解答好本类题目的经验:
1.数列收敛,则它必定有界。
2.数列有界,未必收敛。
本题型的例子(解答中需要注意的地方用红笔标出)
解答这类题的步骤与经验总结:
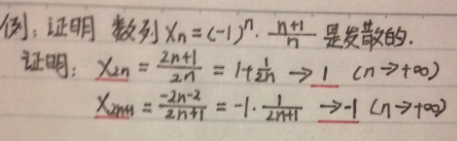

声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:76
阅读量:59
阅读量:154
阅读量:116
阅读量:52