Mathematica基础——处理素数问题

这里，学一些关于Mathematica对数论问题的处理方法。

工具/原料

电脑

Mathematica

内容

整数的素因子分解：FactorInteger。

FactorInteger[2^100 + 1]

这个数字的所有的素因子都是一个，也就是说，任何平方数都不能整除2^100 + 1。

把2^100 + 1的所有素因子用乘式的形式显示出来：

CenterDot @@ (Superscript @@@ FactorInteger[2^100 + 1])

其中，Superscript是“角标”的意思，CenterDot表示“点乘”。

Prime[n]，求第n个素数。比如，求第99999个素数：

Prime[99999]

但是，第2^100 + 1个素数却超出了Mathematica的能力：

Prime[2^100 + 1]

注意：Primes表示“素数域”。

判断一个整数是否是素数：PrimeQ。

在Mathematica里面，默认素数的相反数也是素数。

如：1236971不是素数，但是72763和-72763都是素数，因为72763是1236971的素因子。

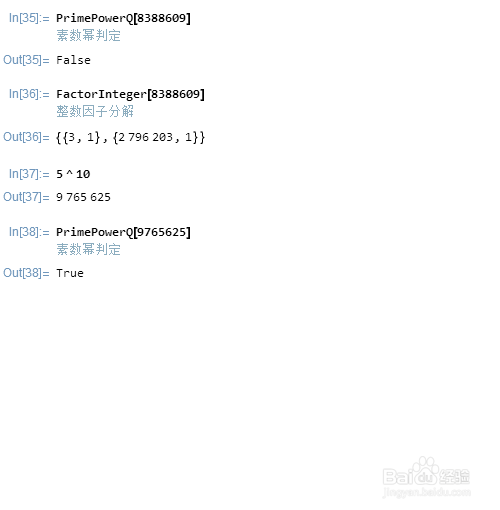
PrimePowerQ[8388609]，判断8388609是否是一个素数的幂，8388609不是素数幂，因为它有两个不同的素因子。

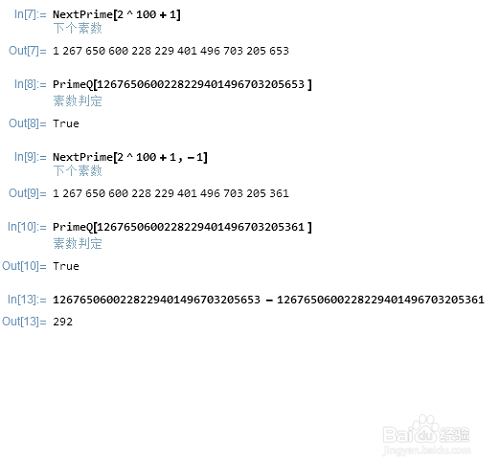
NextPrime[n]：求大于n的最小素数。比如，要知道2^100 + 1的下一个素数：

NextPrime[2^100+1]

NextPrime[n,-1]：求大于n的最小素数。比如，要知道2^100 + 1的上一个素数：

NextPrime[2^100+1,-1]

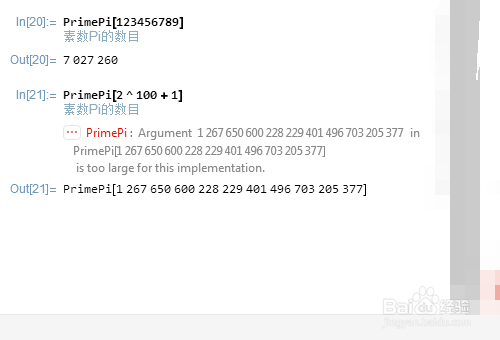
给出小于数字n的素数的个数：PrimePi[n]。

比如，我们想知道123456789以内，有多少个素数：

PrimePi[123456789]

但是，2^100+1以内有多少素数，却是Mathematica能力之外的！

注意事项

素数的相关函数还有很多！