高中物理——曲线运动
1、一.曲线运动
知识点概述
1.曲线运动:物体的轨迹是一条曲线,物体所作的运动就是曲线运动。
作曲线运动物体的速度方向就是曲线那一点的切线方向,而曲线上各点的切线方向不同,也就是运动物体的速度在不断地改变,所以作曲线运动的物体速度是变化的,物体作变速运动。
运动物体的轨迹是它在平面坐标系中的运动图像,与作直线运动物体的位移与时间图像是有着本质的不同,前者是运动的轨迹,后者是其位移随时间变化的规律;前者各点的切线方向是运动物体的速度方向,切线的斜率是运动物体的速度方向与某一方向的夹角的正切,后者各点的切线的斜率是运动物体的速度大小,但它只反映作直线运动物体的速度情况,而不能反映作曲线运动的速度情况。
物体作曲线运动的条件:物体所受的合外力与物体的速度不在一条直线上(也就是合外力沿与速度垂直的方向上有分量,该分量时刻在改变着运动物体的速度方向)
2.运动的合成与分解:运动的合成与分解就是矢量的合成与分解,它涉及运动学中的位移、速度、加速度三个矢量的合成与分解。
两个互相垂直方向上的直线运动合成后可能是直线运动,也可能是曲线运动,反过来,两个方向的直线运动合成后可能是曲线,这就提供了研究曲线运动的途径——将曲线运动转化为直线运动进行研究。
运动的独立作用原理:如同力的独立作用原理一样,运动的合成与分解也是建立在各个方向分运动独立的基础上。
3.研究曲线运动的方法:利用速度、位移、加速度和力这些物理量的矢量性,进行合成与分解。
(1)在恒力的作用下的曲线运动:这种运动是匀速运动。一般将运动物体的初速度沿着力的方向和与力垂直的方向上分解,在沿力的方向上物体作匀变速直线运动,在与力垂直的方向上物体作匀速直线运动。
若所求方向与速度和力均不在一条直线上,将速度和力均沿求解问题的方向和与求解问题垂直的方向进行分解。
(2)在变力作用下的曲线运动:这种运动是非匀变速运动。一般将物体受到的力沿运动方向和与运动垂直的方向分解。与运动方向一致的力改变速度的大小,与运动方向垂直的力改变运动的方向。
生活中的曲线运动举例
子弹射出枪膛,离弦的箭,抛铅球,投篮,过河的船等等都属于曲线运动。
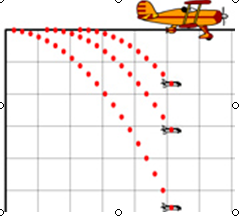
2、二.平抛物体的运动
知识点概述
1.平抛运动的特点:
(1)物体作平抛运动受力特点:它在空中仅受重力作用,重力是恒力,物体只具有重力加速度。
(2)物体作平抛运动的运动特点:物体的初速度水平,与重力垂直,在水平方向不受外力,物体作匀速直线运动,竖直方向作自由落体运动。
平抛运动是匀变速曲线运动。
2.平抛运动的规律:作平抛运动的物体在水平方向上速度不变,在竖直方向上的加速度为重力加速度,以抛出点为原点,以初速度的方向为x轴正方向,以竖直向下为y轴正方向。
(1)位移关系:
水平位移x=v0t ① 竖直位移y=gt2 ②
位移s= ③
位移s与水平夹角为α,tanα== ④
(2)速度关系:
水平速度vx=v0t ⑤ 竖直速度vy=gt ⑥
速度v=√vx2+vy2 ⑦
速度v与水平夹角θ,tanθ===2tanα ⑧
(3)平抛运动的轨迹方程:由①②两式消去时间t得y=*x2
平抛运动中在任何Δt时间内速度的改变量Δv=gΔt,其方向总是向下的。在平抛运动中,当前面无障碍时,物体飞行时间仅决定于飞行高度,一般情况下,当物体离地面高度h为已知时,物体飞行时间为t=。
扩展
作平抛运动的物体,其平抛运动中的水平距离与抛出时的初速度有关,当运动物体的速度改变,其运动过程中的水平距离也将发生变化;当作平抛运动的物体与其运动的物体相遇时,往往是利用它们的位置相同时的位移关系求解;当作平抛运动的物体的速度方向一旦确定,也就可以确定其运动的时间或位移,主要类型如下:
1.一个物体作平抛运动,当它的受力情况发生了变化,则运动状态也发生了变化,当物体是由两段不同的运动形式所构成,那么前阶段的速度就是后阶段的初速度,作平抛运动的末速度就是后阶段其他运动的初速度。
2.作平抛运动的物体,它轨迹由初速度和阻碍物(离地面的高度、斜面、墙壁、排球网……)所决定,反过来,阻碍物也导致了作平抛运动的物体具有临界状态。
3.相遇问题与相遇两个物体的运动情况有关,扣住相遇物体的位置相同是基本点,位移与相对距离的关系,可从分运动的角度考虑,也可以从合运动的角度考虑。
4.研究平抛运动时,并不都是从水平和竖直两个方向进行研究,所以,在曲线运动的研究方法中,就注意到沿所求解物理量的方向与该方向垂直的两个方向进行分解才是分解的唯一原则。
生活中的平抛运动举例
摆球在竖直平面内绕悬点摆动,摆到最低点时绳突然断裂,此后摆球所做的运动;雨伞绕竖直轴转动,伞边缘的水滴甩出后所做的运动(不计空气阻力)从枪口射出的子弹,从飞机上抛下的物体等。
实例分析一
1945年8月6日,美国轰炸机向广岛投下代号为Boy的原子弹,原子弹是核武器之一,是利用核反应的光热辐射、冲击波和感生放射性造成杀伤和破坏作用,以及造成大面积放射性污染,阻止对方军事行动以达到战略目的的大杀伤力武器。
在日本战败已成定局的前提下,没过仍然于8月6日、9日先后在日本的广岛和长崎投下了仅有的两颗原子弹。并通过精密的计算,精准打击了目标。
事后,我们不仅仅为原子弹的威力感到震惊,同时也赞叹于其精准的打击能力,通过对飞机投放出的原子弹所行进的轨迹,我们不难看出,它是一个平抛运动,原子弹在出仓时,在水平方向上拥有一个初速度,并且在出仓后水平方向无外力作用,在竖直方向上,原子弹出仓时初速度为零,并且在出仓后只受重力作用,是原子弹在竖直方向上作着自由落体运动,最终精准打击目标。
实例分析二
下雨天,然们为了避免挨浇,都要打着伞出门,在到达目的地后,我们经常会看见大部分人会把伞撑起然后进行转动,落在上面的雨滴就从伞的边缘被甩出,而雨伞也很快就会变干,细心的人们就会发现,其实雨滴被甩出之后,雨滴所做的运动就是一个类平抛运动。
我们可以将这个类平抛运动做的理想化一些,一个平整的没有弧度的雨伞表面,水平放置,我们转动伞柄,慢慢会发现落在伞面的雨滴受到离心力作用会慢慢的跑向雨伞边缘,最终沿着雨伞边缘的切线方向被甩出,甩出时雨伞获得了圆周运动时所具有的初速度,并在甩出后水平方向没有外力的干饶,竖直方向,甩出后,雨滴只受重力作用,做自由落体运动,其运动轨迹就是一个平抛运动的抛物线轨迹。
3、三.圆周运动
知识点概述
1.圆周运动:质点的运动轨迹是圆周的运动。
2.匀速圆周运动:质点的轨迹是圆周,在相等的时间内,通过的弧长相等,质点所作的运动是匀速率圆周运动。
3.描述匀速圆周运动的物理量
(1)周期(T):质点完成一次圆周运动所用的时间为周期。
频率(f):1s钟完成圆周运动的次数。f=
(2)线速度(v):线速度就是瞬间速度。做匀速圆周运动的质点,其线速度的大小不变,方向却时刻改变,匀速圆周运动是一个变速运动。
由瞬时速度的定义式v=,当Δt趋近于0时,Δs与所对应的弧长(Δl)基本重合,所以v=,在匀速圆周运动中,由于相等的时间内通过的弧长相等,那么很小一段的弧长与通过这段弧长所用时间的比值是相等的,所以,其线速度大小v=(其中R是运动物体的轨道半径,T为周期)
(3)角速度(ω):作匀速圆周运动的质点与圆心的连线所扫过的角度与所用时间的比值。ω==,由此式可知匀速圆周运动是角速度不变的运动。
4.竖直面内的圆周运动(非匀速圆周运动)
(1)轻绳的一端固定,另一端连着一个小球(活小物块),小球在竖直面内作圆周运动,或者是一个竖直的圆形轨迹,一个小球(或小物块)在其内壁上作竖直面的圆周运动,然后进行计算分析,结论如下:
①小球若在圆周上,且速度为零,只能是在水平直径两个端点以下部分的各点,小球要到达竖直圆周水平直径以上各点,则其速度至少要满足重力指向圆心的分量提供向心力
②小球在竖直圆周的最低点沿圆周向上运动的过程中,速度不断减小(重力沿运动方向的分量与速度方向是相反的,使小球的速度减小),而小球要到达最高点,则必须在最低点具有足够大的速度才能到达最高点,否则小球就会在圆周上的某一点(这一点一定在水平直径以上)绳子的拉力为零时,小球就脱离圆周轨道。
(2)物体在杆或圆管的环形轨道上作竖直面内圆周运动,虽然物体从最低点沿圆周向最高点运动的过程中,速度越来越小,由于物体可以受到杆的拉力和压力(或圆管对它的向内或向外的作用力),所以,物体在圆周上的任意一点的速度均可为零。
(3)物体在竖直的圆周的外壁运动,此种运动的关键是要区别做圆周运动和平抛运动的条件,它们的临界状态是物体的重力沿半径的分量提供向心力,此时,轨道对物体没有作用力,但物体又在轨道上,该点是物体在圆周上的临界点。若物体在最高点时,mg=,v0=,当v≥v0,物体在最高点处将作平抛运动,当v<v0,物体将沿圆周轨道下滑(下滑到一定位置还是要离开轨道)
扩展
竖直面内的圆周运动,只要求讨论分析最高点和最低点的情况,由于最高点的相信加速度竖直向下,质点总是处于失重状态;最低点的向心加速度竖直向上,质点总是处于超重状态,从这个角度来理解竖直面内做圆周运动的质点受力情况比较直观。
质点在圆轨道外圆时,最高点处是作平抛运动还是圆周运动,质点与轨道之间的作用力为零对应的速度是临界速度,这个临界速度就是在圆周上的向心加速度等于重力加速度,质点的速度小于这个速度,受轨道的支持力,大于这个速度,质点作平抛运动。
生活中的圆周运动举例
详见第五小节——生活中的圆周运动
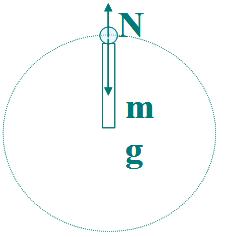
4、四.向心力、向心加速度
知识点概述
1.向心力(Fn):改变速度方向所需要的外力。
向心力是根据力的作用效果命名的。向心力可能是弹力、摩擦力或重力提供,也可能是几个力的合力,还可能是某个力的分力提供。
匀速圆周运动的速率不变,而速度方向时刻在变化,只改变速度方向的力叫做向心力。
向心力最显著的特点是与速度方向垂直,只改变速度方向,不改变速度大小。
作匀速圆周运动的物体,由于速度大小不变,速度方向不断改变,合力一定与速度方向垂直,且合力指向轨迹弯曲一侧,正好指向圆心,所以,将改变速度方向的力称为向心力。
作匀速圆周运动的质点,合外力提供向心力;作非匀速圆周运动的物体来讲,一般将其所受的力沿着运动方向和与运动垂直的方向进行分解:沿运动方向的力(称为切向力)是改变速度大小;沿与运动方向垂直的力(称为法向力)是改变速度的方向。
2.向心加速度(an):向心加速度是由向心力所产生的加速度。源于向心力只改变质点的速度方向,而不改变速度大小,且其方向始终指向轨迹的圆心,由加速度与外力的关系可知向心加速度也是与速度垂直,只改变速度方向,且指向圆心,作匀速圆周运动的质点,速度大小不变,质点只具有向心加速度。
经分析推导过程可知向心加速度是瞬时加速度,不是平均加速度。公式a=是平均加速度,在匀变速直线运动中加速度是不变的,所以平均加速度与加速度的瞬时值相等。
在匀速圆周运动中,ω===2πf
an==ω2R=vω,这一组公式对非匀速圆周运动也适用
an=R=4π2f2R,这一组公式只适用于匀速圆周运动。
扩展
向心力与速度方向垂直,它改变速度方向不改变速度大小。在研究物体作曲线运动时,所采用的途径一般情况下是将物体受的力沿速度方向与速度处置的方向分解,沿速度方向的力一般称为切向力,它改变速度的大小,垂直方向的力一般称为法向力,它改变速度方向,只要是改变速度方向的力都是向心力,所有做曲线运动的物体需要向心力。
向心力的速度是瞬时改变的,所有的钱运动,在每一点都有一个圆心,只有圆周上的各点圆心都重合,而其他曲线各点的圆心没有重合而已,学习向心力和向心加速度后,物体作平抛运动,其轨迹上的各点所对应的半径可求,相应的圆心也可以求出来,这是用物理方法求半径和圆心。
生活中的应用
案例分析一
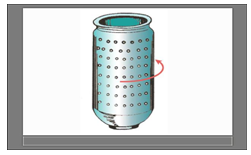
医院内病人做尿检查时,化验员将尿放入试管,并将试管放在一个高速旋转的器材中,经过一段时间后,将试管取出来,发现问题尿的杂质都会沉淀到试管底部,这是为什么呢?
试管高速旋转后,尿中的杂质能很快地沉淀到试管的底部,选取尿中杂质微粒,将杂质微粒换成相同体积的尿来代替,显然,试管高速旋转时尿微粒是不会作离心运动的,而是相对试管静止,这是周围的尿对这尿微粒的合力刚好提供尿微粒作圆周运动的向心力,将尿微粒换回杂质微粒后作匀速圆周运动,由于杂质的质量比尿大,由公式F=mrω2可知,在半径和角速度相同的情况下,向心力与质量成正比,所以,合外力不足以提供杂质所需要的向心力,杂质做远离圆心的运动而沉到试管底部。
案例分析二
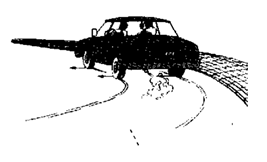
摩托车越野比赛时,经常看到摩托车在转弯处出现翻车现象,这种现象是怎样产生的?怎么样回避这种事故的发生?
摩托车转弯处速度过大,半径过小,由向心力公式F=m可知所需的向心力很大,这是摩托车受到地面的摩擦力达到最大时都不足以提供向心力,摩托车要作远离圆心的运动,向外翻滚。这就说明摩托车在转弯时,速度要小,半径要大,才能保证不出现交通事故,实际上所有的交通工具在转弯时速度都不大,超过转弯的规定速度都有出现交通事故的可能性。
案例分析三
平时我们换洗下来的衣物,在线、清洗之后会放入甩干桶,甩过之后的衣物就很容易晾晒干,这是为什么呢?
当甩干桶得比较慢时,水滴跟物体的附着力F 足以提供所需的向心力F 使水滴做圆周运动。当甩干桶得比较快时,附着力F 不足以提供所需的向心力F,于是水滴做离心运动,穿过桶孔,飞到甩干桶外面。
案例分析四
在医院我们经常看到医生用离心机把体温计的水银柱甩回玻璃泡内,这是如何做到的呢?
当离心机转得比较慢时,缩口的阻力F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。当离心机转得相当快时,阻力F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
案例分析五
制作“棉花”糖的原理
内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
5、五.生活中的圆周运动
实例分析一
火车是目前长距离运输中重要的交通工具,近年来建设铁路新干线较多,铁轨是比较平直的,在转弯处,火车只有依靠与它接触的铁轨提供向心力。工字形铁轨固定在水泥基础上,火车的两轮都有轮缘,突出的轮缘一般起定位作用,若是平直的轨道转弯,只有依靠轨道与轮缘间侧向弹力使火车转弯,由于火车速度大,质量也大,所需要的向心力很大,所以,轮缘与铁轨间的弹性大形变量也大,从而使铁轨容易受到损坏,使火车转弯时的向心力不是由轮缘和轨道间侧向弹力提供,而是由车轮与轨道间正向弹力提供,车轮与轨道间的正向接触面积大,对轨道的影响小,有什么办法可以达到此目的呢?
在牛顿运动定律中,放在光滑斜面上的物体,当斜面以一定加速度作水平运动时,物体可以相对斜面静止,这时斜面的弹力与物体的重力的合力沿水平方向提供加速运动所需要的力(也可以认为斜面的弹力在竖直方向分量与物体的重力平衡,水平方向分量提供物体作加速度所需要的力)从这个例子中,我们能得到的启示是火车转弯时将轨道平面倾斜。
在设计转弯的轨道时,若将外轨垫高些,使轨道平面与水平面有一夹角α,正向压力垂直于轨道平面,要使正向压力在竖直方向分量与重力平衡,水平方向分量提供向心力,则
mgtanα=mv0=
火车以速度v0=行驶时,火车的车轮的轮缘与铁轨的侧向无压力。
火车转弯时,当火车的速度v>v0时,即重力和轨道的支持力的合力不足以提供向心力,需要外轨对外轮的轮缘一个向内的侧压力,补充不充足的向心力;当火车速度v0<v时,重力和轨道的支持力的合力大于向心力,需要内轨对内轮的轮缘一个向外的侧压力,与多余的部分分力平衡。
实例分析二
汽车在水平路面上转弯时依靠静摩擦力提供向心力,在高速公路上,由于汽车的速度比较大,仅靠静摩擦力提供向心力是不行的,所以,在转弯处的路面都是倾斜的(倾角α),若汽车依靠重力和路面支持力的合力提供向心力,就对应的速度如火车转弯是一样的,对应原速度v0=。
当汽车的速度v0≠,路面再施加静摩擦力来作补充。
案例分析三
在杂技表演中,我们曾看见演员用一致小桶装上水,然后用一根长约1米的绳子拴住小桶,使小桶在竖直面内作圆周运动,桶中的水并没有流出,这是什么原因使桶中的水运动到最高点时,水不留出呢?若小桶不能到达圆周的最高点,而是在圆周上的某一点离开圆周,水会不会流出呢?
当小桶在最高点时,水受到重力提供向心力,水是不会流出的,绳子的拉力为零后,桶和水一起作抛体运动,它们的速度一样,加速度一样,他们相对静止,水不会流出桶外,杂技演员只要把桶抛出,水就不会离开桶,我们平时将水泼出,若是将盛水的容器和水一起抛出,水在空中不会离开容器。同理,桶在最高点是静止的,当桶倒置时,水会流出,当水与桶一起倒置时运动到最高点,重力提供加速度,它们是相对静止的且无相无相互作用。
案例分析四
汽车过桥问题
(1)汽车通过拱形桥时,可以看作是一种圆周运动,在最高点时,桥对车的支持力为:
F=G-
又因为汽车对桥的压力和桥对汽车的支持力是一对作用力和反作用力,大小相等,所以压力大小也为:
F=G-
通过以上分析,我们不难看出:
(2)汽车通过凹形桥时,也可以看作是一种圆周运动,在最低点,桥对车的支持力为:
F=G+
又因为汽车对桥的压力和桥对汽车的支持力是一对作用力和反作用力,大小相等,所以压力大小也为:
F=G+
通过以上分析,我们得出如下结论:
案例分析五
飞机在巡逻中,一直在城市的上空水平盘旋做匀速圆周运动,可看见飞机的机身是倾斜的,为什么?
飞机作水平匀速圆周运动时,机身倾斜,空气对机身的合力是与机身垂直,所以,空气对机身的作用力与重力的合力提供向心力,所以机身是倾斜的。
案例分析六
圆锥摆问题
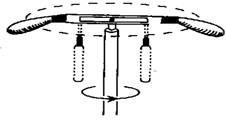
“旋转秋千”中的缆绳跟中心轴的夹角与哪些因素有关?体重不同的人坐在秋千上旋转时,缆绳与中心轴的夹角相同吗?
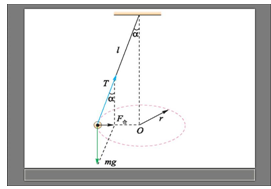
“旋转秋千”的运动经过简化,可以看做如下的物理模型:在一根长为l的细线下面系一根质量为m的小球,将小球拉离竖直位置,使悬线与竖直方向成α角,给小球一根初速度,使小球在水平面内做圆周运动,悬线旋转形成一个圆锥面,这种装置叫做圆锥摆
通过对小球的受力分析,缆绳与中心轴的夹角跟“旋转秋千”的角速度和绳长有关,而与所乘坐人的体重无关,在绳长一定的情况下,角速度越大则缆绳与中心轴的夹角也越大。
案例分析七
航天器中的失重现象:有人把航天器失重的原因说成是它离地球太远,从而摆脱了地球引力,这是错误的。正是由于地球引力的存在,才使航天器连同其他的乘员有可能做环绕地球的圆周运动。这里的分析仅仅针对圆轨道而言。其实任何关闭了发动机,又不受阻力的飞行器的内部,都是一个完全失重的环境。