怎么用Kronecker符号来绘制的“龙”曲线？

1、Mathematica里面，Kronecker符号用KroneckerSymbol来表示。

下图是m从1到600，Kronecker符号(-1丨m)的取值情况。

2、假设一只蚂蚁位于原点，头朝向x轴正方向：

第一次，碰到Kronecker符号(-1丨1)=1，就向左转90°，并前进一步；

第二次，碰到Kronecker符号(-1丨2)=1，再向左转90°，并前进一步；

第三次，碰到Kronecker符号(-1丨3)=-1，就向右转90°，并前进一步；

第四次，碰到Kronecker符号(-1丨4)=1，就再向左转90°，并前进一步；

……

依此类推。

用点代替蚂蚁，折线段代替蚂蚁的移动轨迹，那么，前10步，蚂蚁的移动轨迹如下。

3、前30步的移动轨迹，如下图。

4、用Graphics作图，最大的好处是，可以自动的对成图进行合适的缩放，且保持实际比例。

前100步，轨迹如下，与前图对比，可以看到，折线段的长度越来越短。

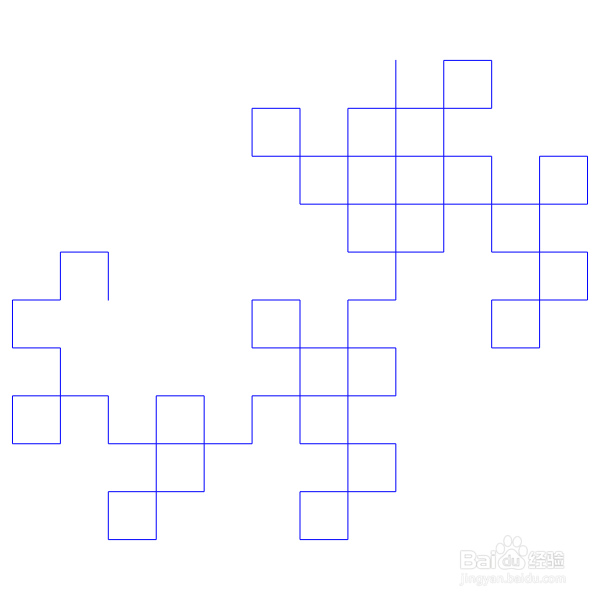
5、前600步，蚂蚁轨迹更密集，折线段也更短了。

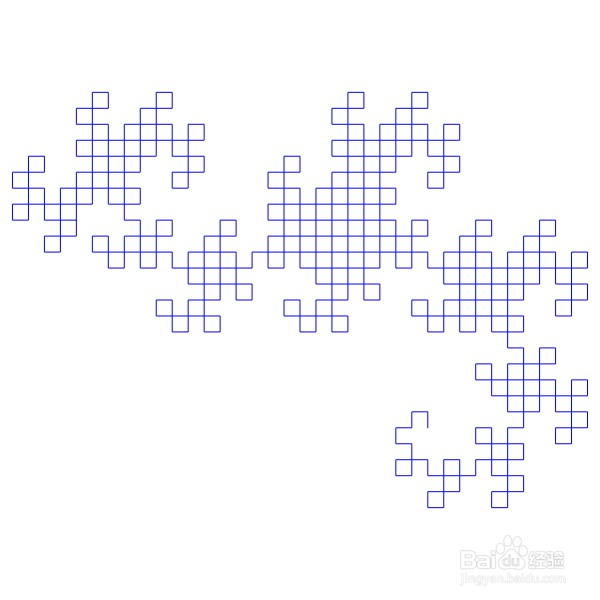
6、前1666步，图形如下。

此时，是不是隐隐约约有一点规律了呢？

7、继续。

前6666步，图形如下，可以看出明显的自相似结构。

8、下图是前10606步的情形。

9、前30000步，看起来，已经具备分形的特征了，细节越来越模糊，而自相似性也很明显。

10、前60000步，比较考验电脑的性能。

下图，分别是60000步、100000、300000、600000步对应的情形。