用Mathematica绘制四维空间的物体

2025-10-26 00:32:58

1、打开Mathematica，新建笔记本，输入如下代码：

v = Tuples[{-1, 1}, 4];

e = Select[Subsets[Range[Length[v]], {2}],

Count[Subtract @@ v[[#]], 0] == 3 &];

f = Select[Union[Flatten[#]] & /@ Subsets[e, {4}], Length@# == 4 &];

f = f /. {a_, b_, c_, d_} :> {b, a, c, d};

rotv[t_] = (RotationMatrix[

t, {{0, 0, 1, 0}, {0, 1, 0, 0}}].RotationMatrix[

2 t, {{1, 0, 0, 0}, {0, 0, 0, 1}}].#) & /@ v;

proj[t_] := Most[#]/(3 - Last[#]) & /@ rotv[t];

Animate[Graphics3D[

GraphicsComplex[

proj[t], {Blue, Specularity[0.75, 10], Sphere[Range[16], 0.05],

Tube[e, 0.03], Opacity[0.3], Polygon@f}], Boxed -> False,

Background -> Orange, ImageSize -> 390, PlotRange -> 1], {t, 0.0,

Pi/2.0, 0.075}]

运行以后，就会得到一个“四维立方体”，呵呵，其实就是动态图。

用Mathematica绘制四维空间的物体

2、导出动态图的代码如下：

v = Tuples[{-1, 1}, 4];

e = Select[Subsets[Range[Length[v]], {2}],

Count[Subtract @@ v[[#]], 0] == 3 &];

f = Select[Union[Flatten[#]] & /@ Subsets[e, {4}], Length@# == 4 &];

f = f /. {a_, b_, c_, d_} :> {b, a, c, d};

rotv[t_] = (RotationMatrix[

t, {{0, 0, 1, 0}, {0, 1, 0, 0}}].RotationMatrix[

2 t, {{1, 0, 0, 0}, {0, 0, 0, 1}}].#) & /@ v;

proj[t_] := Most[#]/(3 - Last[#]) & /@ rotv[t];

Export["C:\\Users\\Administrator\\Desktop\\超立方体0.gif",

Table[Graphics3D[

GraphicsComplex[

proj[t], {Blue, Specularity[0.75, 10], Sphere[Range[16], 0.05],

Tube[e, 0.03], Opacity[0.3], Polygon@f}], Boxed -> False,

Background -> White, ImageSize -> {500, 500}, PlotRange -> 1], {t,

0.0, Pi/2.0, 0.075}]]

用Mathematica绘制四维空间的物体

3、再来一个互动效果：

IncDim[sg_, d_] := Map[Append[#, d] &, sg, {2}];

DblSegments[l_] := Join[IncDim[l, -1], IncDim[l, 1]];

ConnectPoints[l1_, l2_] :=

Table[{Flatten[l1, 1][[i]], Flatten[l2, 1][[i]]}, {i,

Length[Flatten[l1, 1]]}];

DblConnSegments[l_] :=

Union[ConnectPoints[IncDim[l, -1], IncDim[l, 1]]];

UpDimShape[l_] := Join[DblSegments[l], DblConnSegments[l]];

Sqr = UpDimShape[{{{-1}, {1}}}];

Cube = UpDimShape[Sqr];

Homogen[l_] := Map[Append[#, 1] &, l, {2}];

Tes = UpDimShape[Cube];

R4x[\[Theta]_] := {{1, 0, 0, 0, 0}, {0, Cos[\[Theta]], -Sin[\[Theta]],

0, 0}, {0, Sin[\[Theta]], Cos[\[Theta]], 0, 0}, {0, 0, 0, 1,

0}, {0, 0, 0, 0, 1}}

R4y[\[Theta]_] := {{Cos[\[Theta]], 0, Sin[\[Theta]], 0, 0}, {0, 1, 0,

0, 0}, {-Sin[\[Theta]], 0, Cos[\[Theta]], 0, 0}, {0, 0, 0, 1,

0}, {0, 0, 0, 0, 1}}

R4z[\[Theta]_] := {{Cos[\[Theta]], -Sin[\[Theta]], 0, 0,

0}, {Sin[\[Theta]], Cos[\[Theta]], 0, 0, 0}, {0, 0, 1, 0, 0}, {0,

0, 0, 1, 0}, {0, 0, 0, 0, 1}}

R4k[\[Theta]_] := {{1, 0, 0, 0, 0}, {0, 1, 0, 0, 0}, {0, 0,

Cos[\[Theta]], -Sin[\[Theta]], 0}, {0, 0, Sin[\[Theta]],

Cos[\[Theta]], 0}, {0, 0, 0, 0, 1}}

Rotate4X[l_, \[Theta]_] := Map[R4x[\[Theta]].# &, l, {2}]

Rotate4Y[l_, \[Theta]_] := Map[R4y[\[Theta]].# &, l, {2}]

Rotate4Z[l_, \[Theta]_] := Map[R4z[\[Theta]].# &, l, {2}]

Rotate4K[l_, \[Theta]_] := Map[R4k[\[Theta]].# &, l, {2}]

DropUnit[l_] := Map[Drop[#, -1] &, l, {2}]

RotFigure4[l_, \[Theta]x_, \[Theta]y_, \[Theta]z_, \[Theta]k_] :=

DropUnit[Rotate4K[

Rotate4Z[

Rotate4Y[

Rotate4X[

Homogen[l], \[Theta]x], \[Theta]y], \[Theta]z], \[Theta]k]]

PersPoint[pt_, d_] := Map[#/(Last[pt]/d) &, pt]

Perspective[l_, d_] := Ortho[Map[PersPoint[#, d] &, l, {2}]]

Mtr4[x_, y_, z_,

k_] := {{1, 0, 0, 0, x}, {0, 1, 0, 0, y}, {0, 0, 1, 0, z}, {0, 0, 0,

1, k}, {0, 0, 0, 0, 1}}

Trans5vec[l_, x_, y_, z_, k_] := Map[Mtr4[x, y, z, k].# &, l, {2}]

Trans5[l_, x_, y_, z_, k_] :=

DropUnit[Trans5vec[Homogen[l], x, y, z, k]]

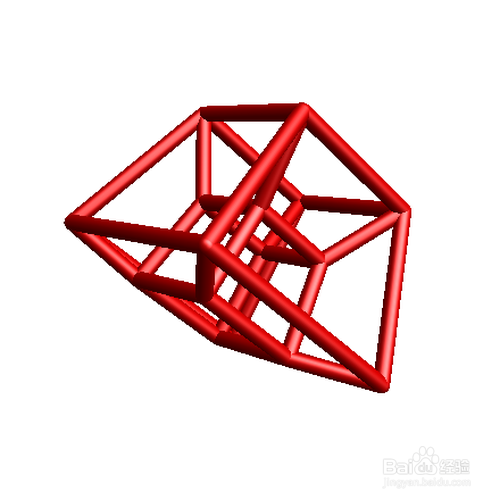
Manipulate[

Graphics3D[{Darker@Red, CapForm["Round"], Specularity[White, 20],

Tube[Perspective[

Trans5[RotFigure4[Tes, 0, 0, 0, a], 0, 0, 0, -3], -1], 0.04]},

PlotRange -> {{-.7, .7}, {-.7, .7}, {-.7, .7}}, Boxed -> False,

Lighting -> "Neutral", ImageSize -> 1.1 {400, 400},

SphericalRegion -> True],

{{a, 0, "动起来"}, 0, 2*3.1416, .0001, Appearance -> "Labeled"},

SaveDefinitions -> True

呵呵，这个动态图的自定义很多，而且我也不会导出动态图！自己慢慢理解吧！

用Mathematica绘制四维空间的物体

4、这里画一个克莱因瓶，这是个四维空间的物体，来源于莫比乌斯带的类比。

Manipulate[

With[{bsc =

Take[{{0, 0, 0}, {0, 0, 14}, {0, 0, 20}, {0, 0, 25}, {1.7, 0,

30}, {7, 0, 32}, {10, 0, 31.5}, {13, 0, 30}, {15, 0, 26}, {13,

0, 20}, {10, 0, 17.5}, {4, 0, 13.5}, {2.5, 0, 11}, {0.33, 0,

7}, {0.2, 0, 2.5}, {0, 0, 0}}, t + 2],

sizes = Take[{6.5, 14, 4, 2.3, 2.2, 2.2, 2.2, 2.2, 2.2, 2.2, 2.2,

2.6, 3.3, 3.6, 4.3, 6.5}, t + 2]},

Graphics3D[{color, CapForm[None], Opacity[opacity],

Tube[BSplineCurve[bsc], sizes]}, Boxed -> False,

PlotRange -> {{-15, 17}, {-15, 15}, {0, 35}},

ViewPoint -> {0, -5, 0}, SphericalRegion -> True,

ImageSize -> {500, 500}]], {{t, 1, "times"}, 1, 14,

1}, {{opacity, 0.7}, 0.1, 1}, {{color, Blue}, ColorSlider}

用Mathematica绘制四维空间的物体

5、把克莱因瓶涂成彩色格子。

KleinBottle[a_, b_, xmesh_, ymesh_] :=

Module[{bx, by, rad, X, Y, Z, u, v},

bx = 6 Cos[u] (1 + Sin[u]);

by = 16 Sin[u];

rad = 4 (1 - Cos[u]/2);

X = If[Pi < u <= 2 Pi, bx + rad Cos[v + Pi],

bx + rad Cos[u] Cos[v]];

Y = If[Pi < u <= 2 Pi, by, by + rad Sin[u] Cos[v]];

Z = rad Sin[v];

ParametricPlot3D[{X, Y, Z}, {u, 0, a}, {v, 0, b},

PlotRange -> {{-13, 10}, {-16, 20}, {-6, 6}},

MeshShading -> {{Red, Blue}, {Green, Yellow}},

MeshStyle -> None,

Axes -> None,

Boxed -> False,

ViewVertical -> {0.44, -0.83, -1.40},

ViewPoint -> {1.62, -0.18, -2.96},

ImageSize -> {425, 425},

Mesh -> {xmesh, ymesh}]

];

Manipulate[

KleinBottle[u, v, a, b], {{u, 2. Pi, "draw"}, 1, 2. Pi,

ImageSize -> Tiny}, {{v, Pi, "cutaway"}, Pi, 2. Pi,

ImageSize -> Tiny}, {{a, 1, "mesh A"}, 1, 8, 1,

ImageSize -> Tiny}, {{b, 1, "mesh B"}, 1, 4, 1, ImageSize -> Tiny},

ControlPlacement -> Left, SaveDefinitions -> True

用Mathematica绘制四维空间的物体

声明：本网站引用、摘录或转载内容仅供网站访问者交流或参考，不代表本站立场，如存在版权或非法内容，请联系站长删除，联系邮箱：site.kefu@qq.com。