MATLAB如何学?怎样快速入门?基础入门实例速学
1、MATLAB 十个基础入门实例详解的 scope

2、实例一:一周温度数据的定义与操作
将一周的温度数据,使用一个矩阵A进行保存
取出星期二中午,星期四早晨,星期日中午和夜晚的温度值
取出矩阵A中的前六个数值(from : step : to)
取出星期二的数据
取出星期二,星期三,以及星期六的数据,组成新的矩阵
求每天温度的平均值
求一周的早晨、中午和夜晚温度的平均值
求一周的温度平均值

3、实例二:坐标点的平移变换
以上的相乘计算均为矩阵乘法(*)
考察两个平移变换矩阵之间的矩阵乘法(*),和数组乘法(.*),看看有何不同?
类似需要区分的矩阵/数组运算还有:除法、乘方
矩阵加减法= 数组加减法,无需区分

4、实例三:MATLAB 常用矩阵示例
zeros: 全0 矩阵
ones: 全1 矩阵
rand: 在0 到1 上,均匀分布的随机矩阵,并绘制数据直方图
randn: 均值为0,方差为1,正态分布的随机矩阵,并绘制数据直方图
eye: 单位矩阵
magic: 魔术矩阵,其行、列和对角线上元素的和相等(用MATLAB 计算)

5、实例四:MATLAB 复数矩阵示例
复数的代数形式:z = a + b * i 或者 z = a + b * j
复数的指数形式:z = A eiθ
计算复数的实部:real (z)
计算复数的虚部:imag (z)
计算复数的模:abs (z)
计算复数的相角:angle (z)

6、实例五:MATLAB 字符矩阵示例
字符串的定义
字符串比较函数:strcmp 与strcmpi的区别
字符串转换成矩阵:str2mat
字符串存储在元胞数组(cell)

7、实例六:线性方程组在 MATLAB 里的求解
改写成矩阵相乘的形式:AX = b
X = A-1b
MATLAB 代码(两种写法)
X = inv(A)*b,其中,inv(A) 表示矩阵A 的逆矩阵A-1
X = A\b (左除)

8、实例七:MATLAB 二维曲线的绘制
定义 x
定义 y1 = sin (x); y2 = cos (x); y3 = sin (x) + cos (x)
plot 函数绘制以上二维曲线
设置坐标轴和图例

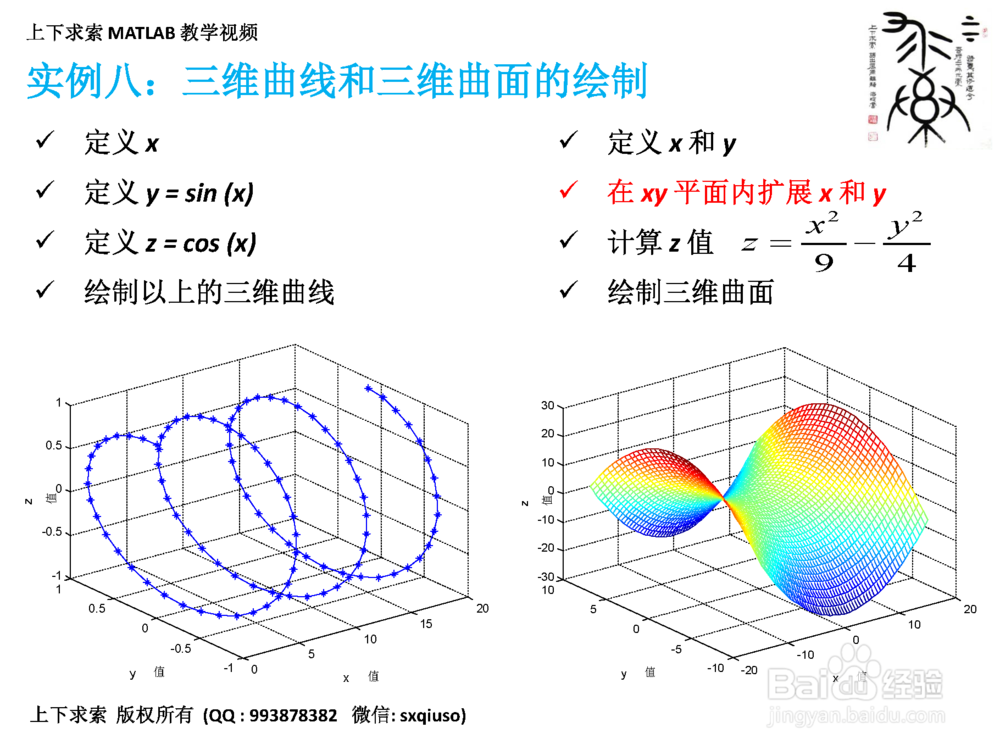
9、实例八:三维曲线和三维曲面的绘制
三维曲线的绘制
定义 x
定义 y = sin (x)
定义 z = cos (x)
plot3 函数绘制以上的三维曲线
三维曲面的绘制
定义 x 和 y
在 xy 平面内扩展 x 和 y
计算 z 值
mesh 函数绘制三维曲面
10、实例九:MATLAB 制作一个简单的动画
绘制一条正弦曲线
在曲线上放置一个红色圆圈,使其在曲线上移动

11、实例十:MATLAB 里函数的定义与调用
定义x = -5 : 0.1 : 5
在脚本script 里编写代码,绘制y = ax3 + bx2 + cx + d 的曲线,并保存y值
a = -1, b = 2, c = -5, d = 3
a = 3, b = -7, c = 1, d = 4
a = 0, b = 4, c = 0, d = -5
将绘图的代码,定义成函数的形式
function[输出变量] = 函数名(输入变量)
直接运行函数,查看报错信息
在脚本script 里调用函数

12、MATLAB 学习的总结与经验分享
通过以上的十个实例,希望可以激发同学们的学习热情,让大家建立起基本的MATLAB 概念
学好MATLAB,还需要勤加练习,多思考,多动手写代码
1. 更多的矩阵操作(数值删除,增加,寻找,排序等)
2. 三维/ 多维矩阵的使用
3. 元胞数组/ 结构体的使用
4. 符号计算的相关内容
5. 流程控制语句
6. 更多种类的图形绘制
7. 句柄操作,等等
