怎样描述函数的单调性

1、一般地，设一连续函数f(x) 的定义域为D，则如果对于属于定义域D内某个区间上的任意两个自变量的值x1，x2∈D且x1>x2，都有f(x1) >f(x2)，即在D上具有单调性且单调增加，那么就说f(x) 在这个区间上是增函数。相反地，如果对于属于定义域D内某个区间上的任意两个自变量的值x1，x2∈D且x1>x2，都有f(x1) <f(x2)，即在D上具有单调性且单调减少，那么就说f(x) 在这个区间上是减函数。则增函数和减函数统称单调函数。[3]

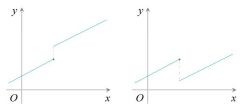
2、函数单调性的几何特征：在单调辨泔矣嚣区间上，增函数的图象是上升的，减函数的图象是下降的。当x1 < x2时，都有f(x1)<f(x2) 等价于 ；当x1 < x2时，都有f烫喇霰嘴(x1)>f(x2) 。如上图右所示，对于该特殊函数f(x)，我们不说它是增函数或减函数，但我们可以说它在区间 [x1，x2]上具有单调性。[1][4]运算性质f(x)与f(x)+a具有相同单调性；f(x)与 g(x) = a·f(x)在 a>0 时有相同单调性，当 a<0 时，具有相反单调性；当f(x)、g(x)都是增（减）函数时，若两者都恒大于零，则f(x)×g(x)为增（减）函数；若两者都恒小于零，则为减（增）函数；[4]两个增函数之和仍为增函数；增函数减去减函数为增函数；两个减函数之和仍为减函数；减函数减去增函数为减函数；函数值在区间内同号时， 增（减）函数的倒数为减（增）函数。[5]

3、图象观察法如上所述，在单调区间上，增函数的图象是上升的，减函数的图象是下降的。因此，在某一区间内，一直上升的函数图象对应的函数在该区间单调递增；一直下降的函数图象对应的函数在该区间单调递减；[1]

4、定义法根据函数单调性的定义，在这里只阐述用定义证明的几个步骤:①在区间D上，任取，令②作差③对的结果进行变形处理(通常是配方、因式分解、有理化、通分，利用公式等等)[5]；④确定符号的正负；⑤下结论，根据“同增异减”原则，指出函数在区间上的单调性。[5]

5、等价定义法设函数的定义域为D，在定义域内任取,，且，若>0，则函数单调递增；若有 <0，则函数单调递减(证明从略)，以上是函数单调性的第二定义。

6、求导法导数与函数单调性密切相关。它是研究函数的另一种方法，为其开辟了许多新途径。特别是对于具体函数，利用导数求解函数单调性，思路清晰，步骤明确，既快捷又易于掌握，利用导数求解函数单调性，要求熟练掌握基本求导公式。如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加；反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。

7、复合函数法在函数y=f[g(x)]的定义域内，令u=g(x)，则y=f[g(x)]的单调性由u=g(x)与y=f(x)的单调性共同确定，方法如下u=g(x)y=f(x)y=f[g(x)]增函数增函数增函数减函数减函数增函数增函数减函数减函数减函数增函数减函数因此，复合函数的单调性可用“同增异减”来判定，但要考虑某些特殊函数的定义域。