在geogebra5中如何用不等式表示圆环

1、在代数区分别输入点A的坐标:

A = (2.62, 1.58)

在代数区分别输入不等式a:

a: (x - x(A))² + (y - y(A))² ≤ 5 ∧ (x - x(A))² + (y - y(A))² ≥ 3

注意:符号∧,∨均在@编辑区完成,得到的圆环如下图所示:

2、在代数区分别输入圆c 的圆心B及圆c圆周上一点C的坐标:

B = (-1.88, -1.84)

C = (-0.1, -2.86)

在代数区分别输入圆d 的圆心D坐标:

D = (-2.46, -2.44)

注意: 圆心B是圆d的圆周上一点,由于圆心B其坐标已输入,所以不用再输入.

如下图霸趴痕所示:

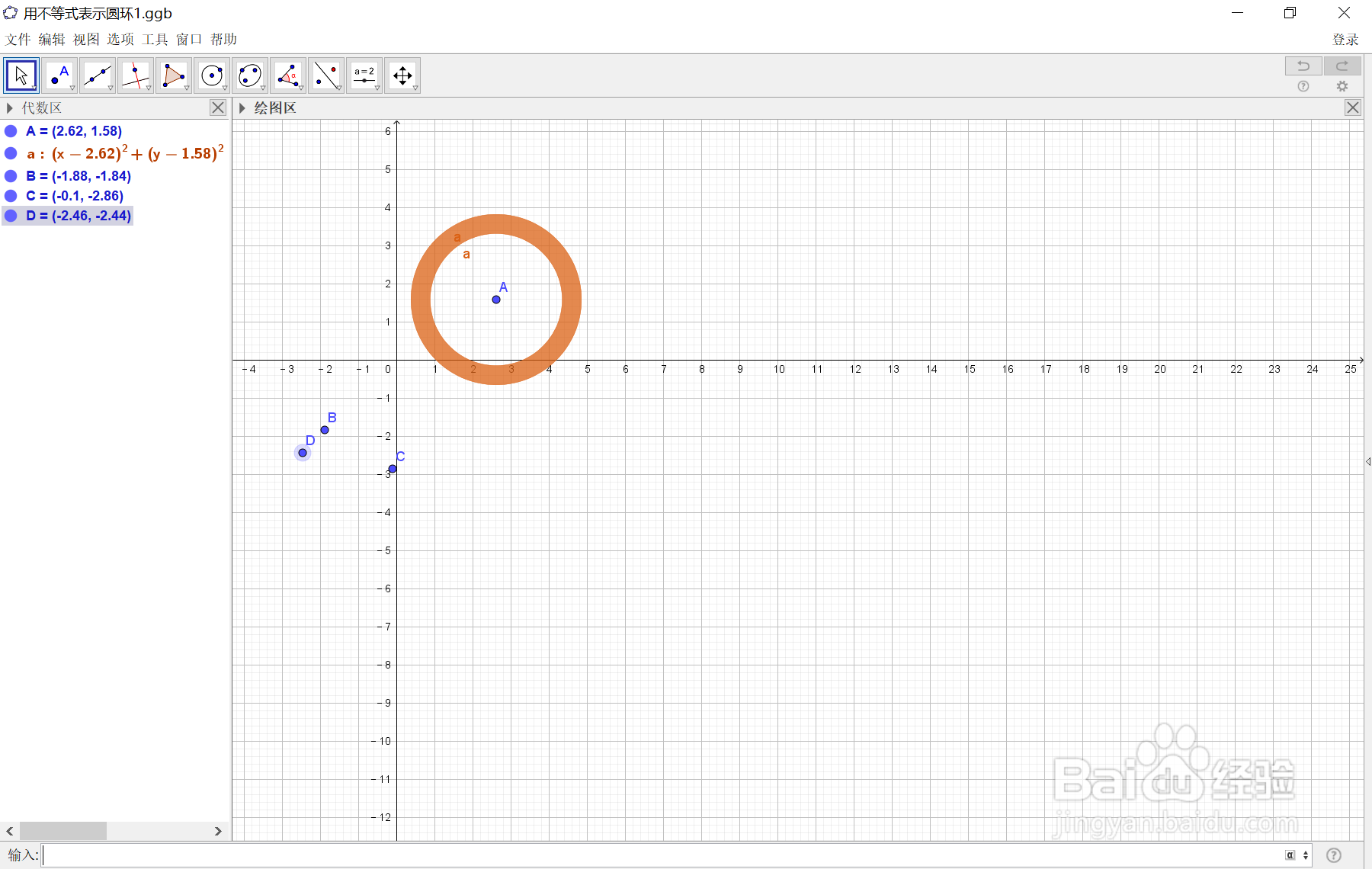
3、在代数区输入圆锥曲线圆c, 圆d的方颂久程式为:

c: Circle(B, C)

d: Circle(D, B)

如下图所示:

4、在代数区输入不等式b的表达式:

b: LeftSide(c) ≤ RightSide(c) ∧墨吐 LeftSide(d) ≥ RightSide(d)

1）当LeftSide（c）≤RightSide（c）时，即所有到圆心距离小于半径的点的集合，即填充c圆内：

2）当LeftSide（d）≥RightSide（d）时，即所有到圆心距离大于半径的点的集合，即填充圆d外,因此，b: LeftSide(c) ≤ RightSide(c) ∧ LeftSide(d) ≥ RightSide(d)，其中公式中"∧ "表示and）

所得圆环如图所示:

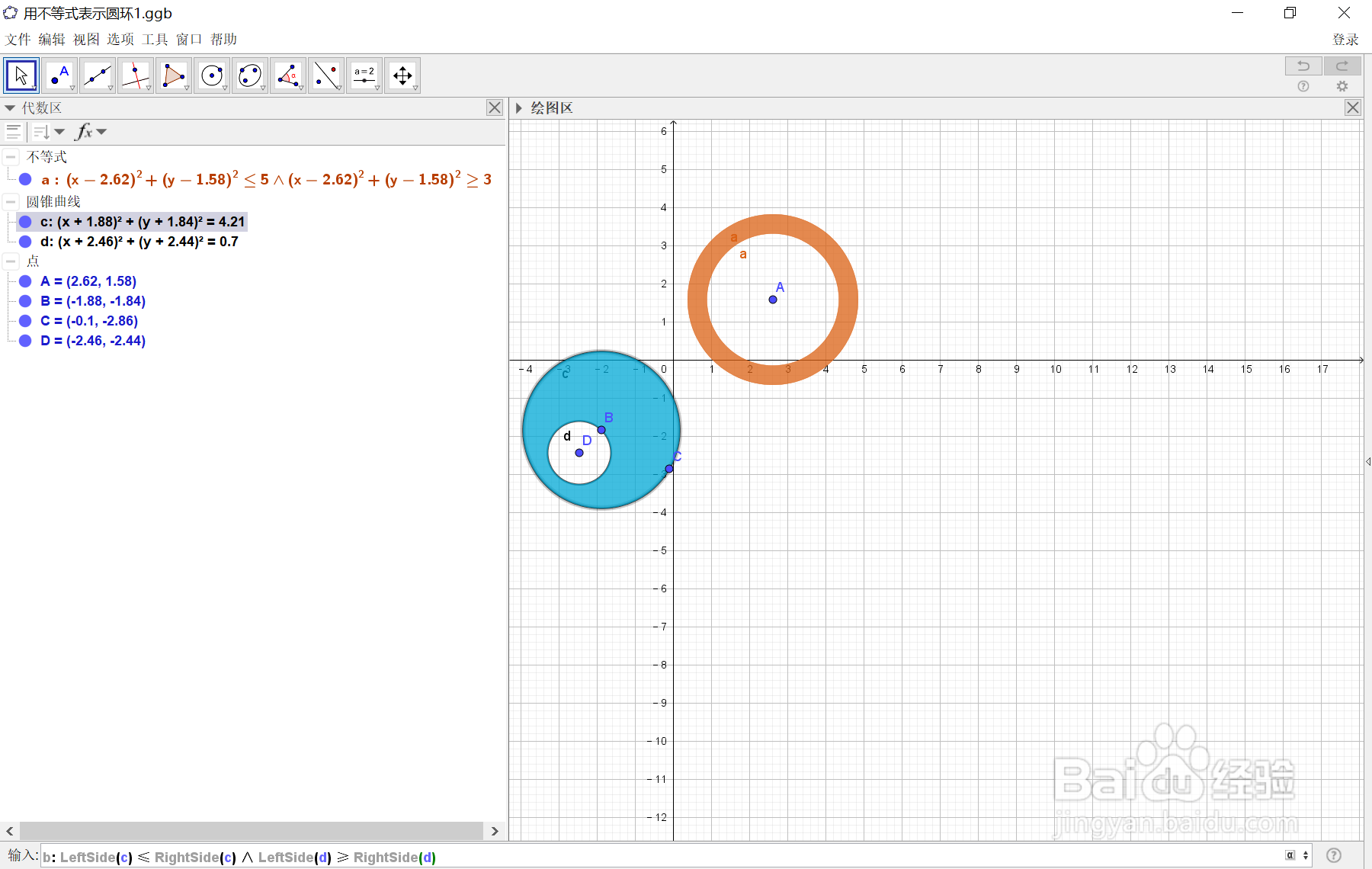
5、如果需要改变由不等式构成的圆环区域颜色,可以先选择需要改变构成的圆环区域,再然后可以通过选择绘图区中的颜色和不透明度就可以了。

如下图所示:

6、最终效果,如下图所示: