如何解析隐函数x^3+y^3=8的主要性质及图像？

1、      本文介绍曲线方程x^3+y^3=8的定义域、单调性、凸凹性等性质，同时用导数的知识求解函数的单调区间和凸凹区间.

2、     根据函数特征，函数自变量可以取全体实数，即定义域为：(-∞，+∞）。

3、函数的凸凹性，通过函数的二阶导数，解析函数的凸凹性。

4、求出函数的拐点，根据拐点，求出函数的凸凹区间。

又因为x^3+y^3=8，则y=3√[(8-x^3)],

代入二阶导数，则：

y’’=(16)*x/3√[(8-x^3) ]^5

=(16)x*3√[1/(x^3-8)^5],

令y’’=0,则x=0，

同时有无穷间断点x=6√2，此时有：

(1)当x∈(-∞，0)，(6√2，∞)时，y’’>0，函数图像为凹函数。

(2)当x∈[0,6√2)时，y’’＜0，函数图像为凸函数。

5、函数五点图，列举隐函数上部分点图表，归纳如下表所示：

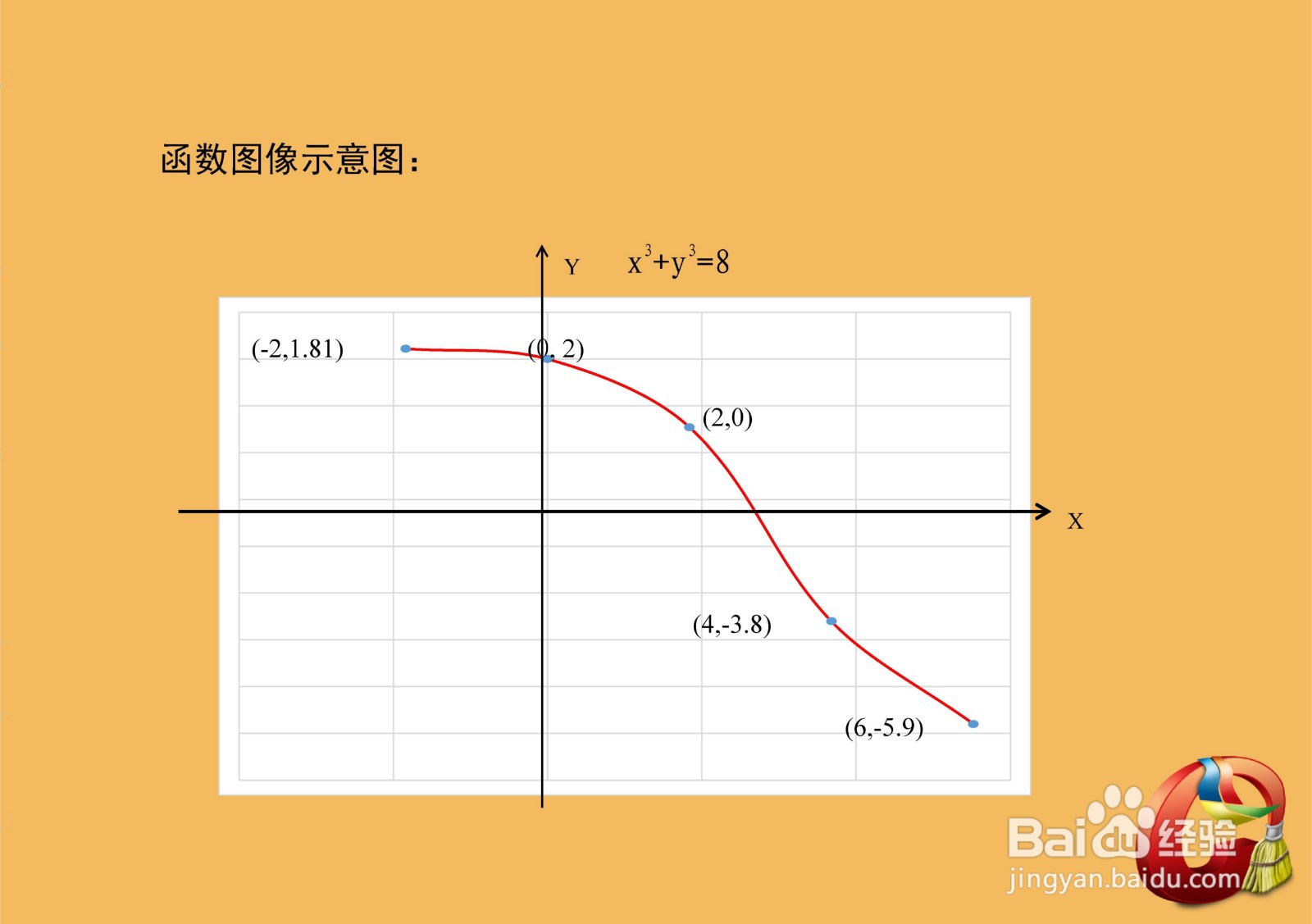
6、综合以上函数的定义域、值域、单调性、凸凹性等性质，函数的示意图如下：

1、     二阶导数，是原函数导数的导数，将原函数进行二次求导。一般的，函数y=f(x)的导数y'=f'(x)仍然是x的函数，则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。

2、    如果函数f(x)在区间I上二阶可导，则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。