高中数学必会裂项相消

1、什么是裂项相消法

数列的裂项相消法，就是把通项拆分成“两项的差”的形式，使得恰好在求和时能够“抵消”多数的项而剩余少数几项。

三大特征：

（1）分子全部相同，最简单形式为都是1的，复杂形式可为都是x(x为任意自然数)的，但是只要将x提取出来即可转化为分子都是1的运算。

（2）分母上均为几个自然数的乘积形式，并且满足相邻2个分母上的因 数“首尾相接” 

（3）分母上几个因 数间的差是一个定值。

裂差型运算的核心环节是“两两抵消达到简化的目的”。

1、基础（1）1/[n(n+1)]=（1/n）- [1/(n+1)]

2、提升（2）1/[(2n-1)(2n+1)]=1/2[1/(2n-1)-1/(2n+1)]

（3）1/[n(n+1)(n+2)]=1/2{1/[n(n+1)]-1/[(n+1)(n+2)]}

（4）1/(√a+√b)=[1/(a-b)](√a-√b)

3、特殊（5）n·n!=(n+1)!-n!

（6）1/[n(n+k)]=1/k[1/n-1/(n+k)]

（7）1/[√n+√（n+1）]=√（n+1）-√n

（8）1/（√n+√n+k）=（1/k）·[√（n+k）-√n]

1、例1

tan 3° tan 63° + tan 63° tan123° + tan123° tan183° =

如图

2、先推个公式（无法打字，就配图了）

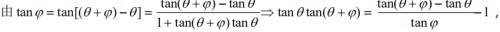
3、所以tan 3° tan 63° + tan 63° tan123° + tan123° tan183° 

     =(tan183°- tan123°+ tan123°- tan 63°+ tan 63°-tan 3°)/   tan 60°-3

     =-3

4、例2

（无法打字，就配图了）

如图

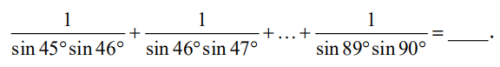
5、解析

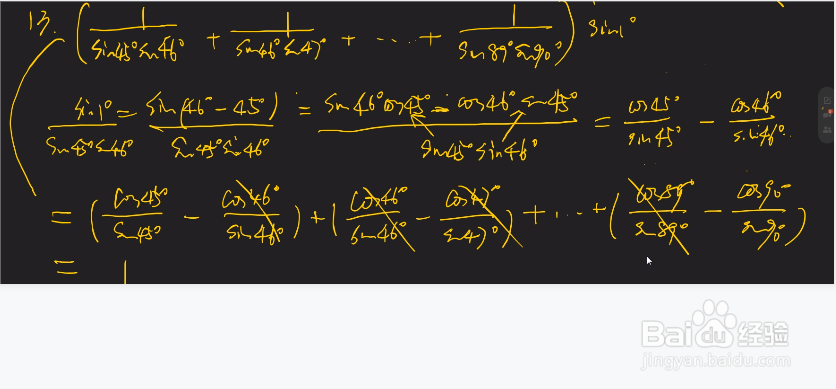
1、多加练习

掌握规律

自然就会

ヾ(◍°∇°◍)ﾉﾞ