遇到(1+ax)^b*(1+cx)d/(1+e(x^f)^g 怎么求极限

2025-07-05 15:46:05

1、当x趋近于无穷，求[(1+2x)^10*(1+3x)^20]/(1+6*x^2)^15的极限

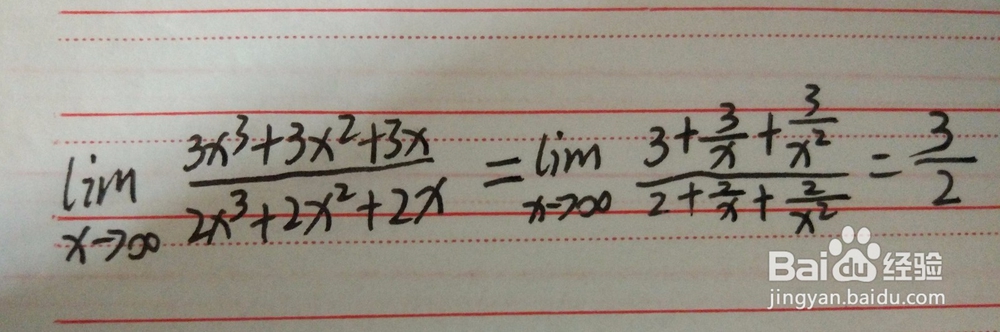
4、所以，由上面可以得到例题的求法就是最高次的系数之比[（2*x）^10*(3*x)^20]-------------------------(6x^2)^15得到极限为243/32

声明：本网站引用、摘录或转载内容仅供网站访问者交流或参考，不代表本站立场，如存在版权或非法内容，请联系站长删除，联系邮箱：site.kefu@qq.com。