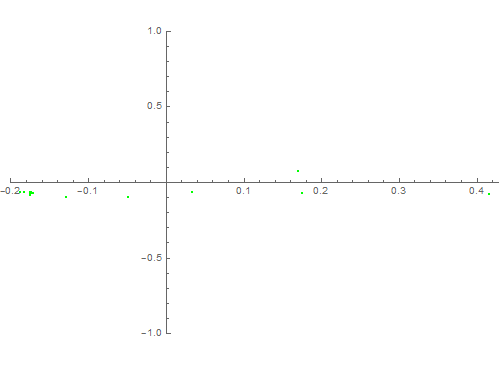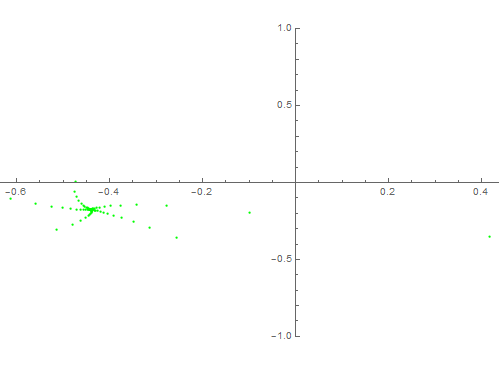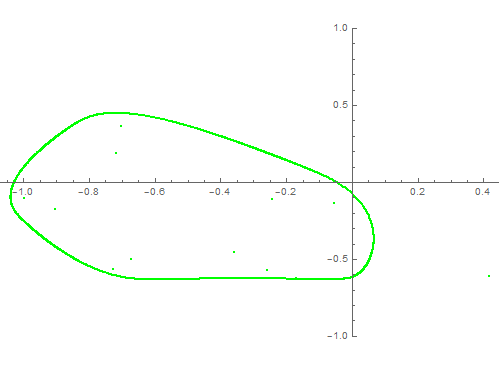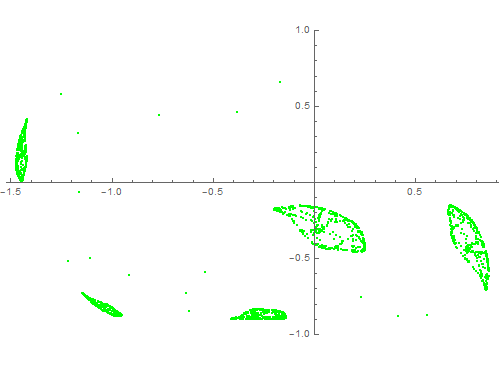Mathematica基础——处理简单的数列问题

1、        以前，总是遇到一些无聊的猜数游戏，比如“1，2，4，9的下一个数是多少”。这种问题是没有明确答案的，比如，我们可以这样提问对方：

        “1，2，4，9，2的下一个数是多少”，

        “1，2，4，9，6的下一个数是多少”，

        “1，2，4，9，21的下一个数是多少”。

        这里，不是批判，而是要看看Mathematica能干什么！

        用FindSequenceFunction [{1,2,4,9},n]可以给出{1,2,4,9}的一个可能最简单的通式，并用DiscretePlot作出图像。

        运行结果里的Hypergeometric2F1是一个超椭圆函数。

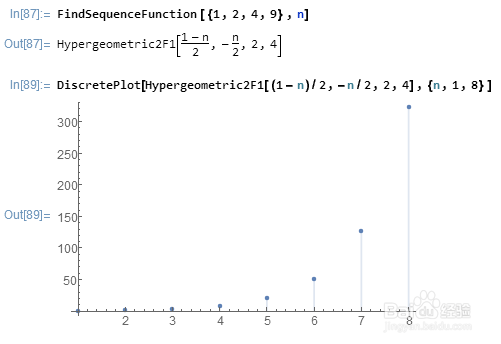
2、        那么，Mathematica给出的{1,2,4,9}的下一个数是多少呢？看图像肯定是不准确的！我们已知四个数，要求第五个数，可以设n为5。

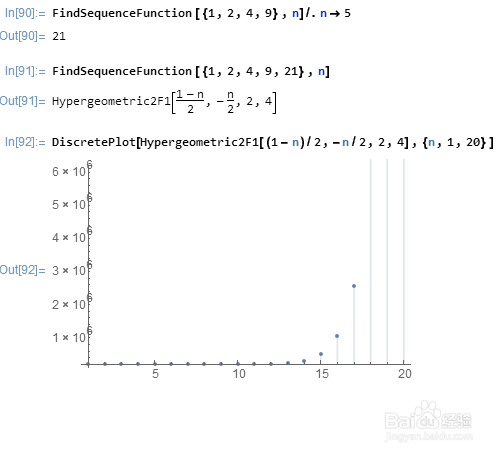
FindSequenceFunction [{1,2,4,9},n]/.n->5

        给出的答案是21。检验一下：FindSequenceFunction [{1,2,4,9,21},n]，可以看到，结果跟FindSequenceFunction [{1,2,4,9},n]完全一样！

        这个数列增长的相当快，当n等于18的时候，数值已经超过了六百万！

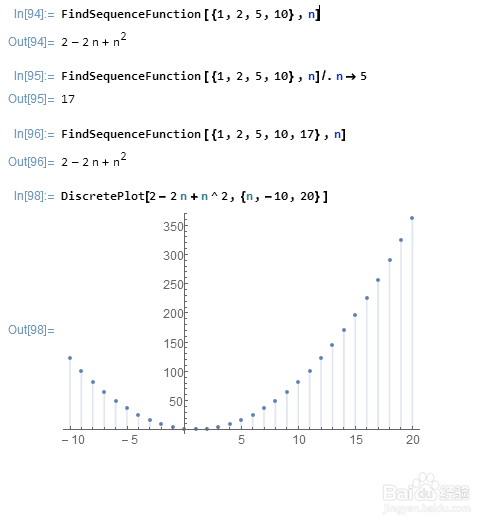
3、        再看一个简单点的栗子：｛1，2，5，10｝下一个是17。

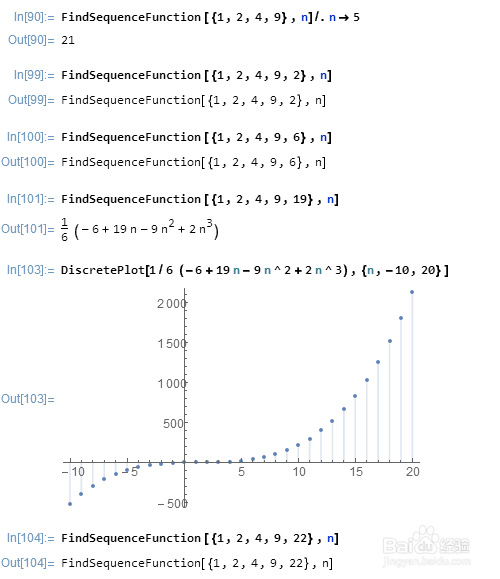
4、        大多数情形，Mathematica也懒得构造通项公式。

        在做实验的时候，发现，Mathematica居然给出了{1,2,4,9,19}的通式(-6+19 n-9 n^2+2 n^3)/6。

        我真是不知道，Mathematica为什么会给出21，而不是19，难道超椭圆函数比三次函数更简单吗？

1、        求递推公式a[n + 1] - 2 a[n] == 1对应的数列的通项公式。

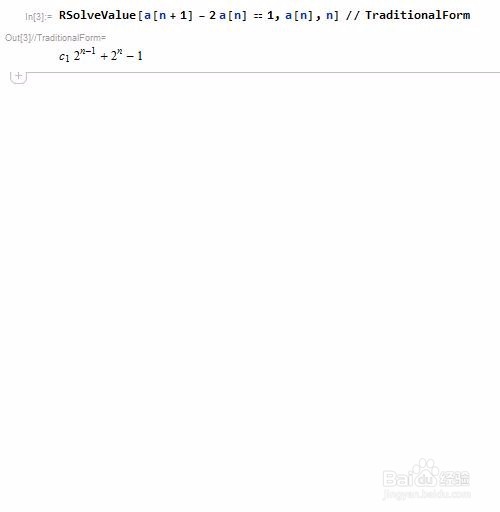
RSolve[a[n + 1] - 2 a[n] == 1, a[n], n]

        给出的通式解是 c1*2^(n-1)+2^n-1，其中，c1是常数。

2、        给出初始条件a[0]==1，就能得到特解：

RSolveValue[{a[n + 1] - 2 a[n] == 1, a[0] == 1}, a[n], n] // TraditionalForm

        这就相当于多求了一个方程的解，得出了c1的值。

3、        更复杂的递推公式a[n + 1] == (2 a[n] + 3)/(a[n] + 4)也能解开：

RSolve[{a[n + 1] == (2 a[n] + 3)/(a[n] + 4), a[0] == 0}, a[n], n]

1、        给出前10个Fibonacci数：

Table[Fibonacci[n], {n, 10}]

        还可以用RecurrenceTable直接发掘通式来求值（但是它不返回通式）：

RecurrenceTable[{a[n]==a[n - 1]+a[n - 2], a[1] == 1,a[2] == 1},a,{n,10}]

        想看通式，可以这样：

RSolveValue[{a[n] == a[n - 1] + a[n - 2], a[1] == 1, a[2] == 1}, a[n],n]

        可惜，Mathematica并不想让我们知道通解是什么！

2、        在a[n]==a[n - 1]+a[n - 2]的基础上，多写一项：

        a[n]==a[n - 1]+a[n - 2]+a[n-3],代码是：

RecurrenceTable[{a[n] == a[n - 1] + a[n - 2] + a[n - 3], a[1] == 1, 

  a[2] == 1, a[3] == 1}, a, {n, 10}]

        但是好像难以求出通解：

RSolveValue[{a[n] == a[n - 1] + a[n - 2] + a[n - 3], a[1] == 1, 

   a[2] == 1, a[3] == 1}, a[n], n] // TraditionalForm

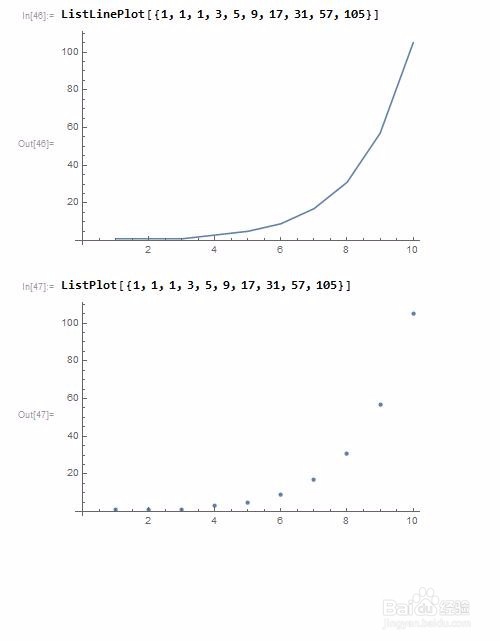
        试着画出图像：

ListPlot[{1, 1, 1, 3, 5, 9, 17, 31, 57, 105}]

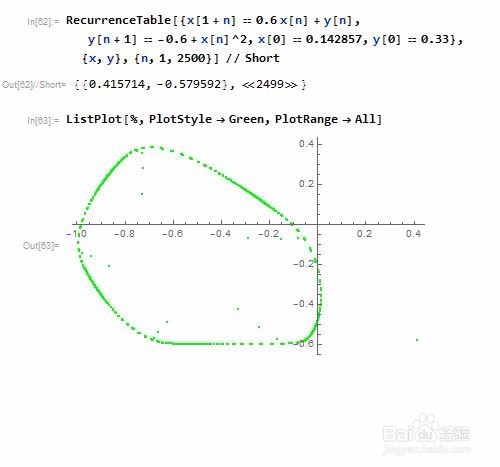
3、        解一个递归方程组：

RecurrenceTable[{

x[1 + n] == 0.6 x[n] + y[n], 

y[n + 1] == -0.6 + x[n]^2,

 x[0] == 0.142857, y[0] == 0.33},

 {x, y}, {n, 1, 2500}] // Short

        作出点的离散图像：

ListPlot[%, PlotStyle -> Green, PlotRange -> All]

4、        制造一个动态效果，实现人机互动：

Manipulate[

 ListPlot[RecurrenceTable[{x[1 + n] == 0.6 x[n] + y[n], 

    y[n + 1] == -t + x[n]^2, x[0] == 0.142857, y[0] == 0.33}, {x, 

    y}, {n, 1, 2500}], PlotStyle -> Green, PlotRange -> {-1, 1}, 

  ImageSize -> {500, 365}], {t, 0.1, 0.9, 0.01}]