splay树操作详解

1、一、二叉搜索树(BST——Binary Search Tree)二叉搜索树是一颗满足如下性质的二叉树：左子树值<=根节点值<=右子树值。因此理论上我们可以在 O(logN)的时间内完成插入、删除、查找等操作。是一种在“动态维护”中效果相当不错的数据结构。但由于题目数据的原因，可能造成二叉查找树并不平衡（严重的时候可能退化为线性），致使插入、删除、查找等操作的复杂度退化为 O(N)。为了尽量保持二叉搜索树的平衡，我们需要去维护二叉搜索树——平衡二叉树。

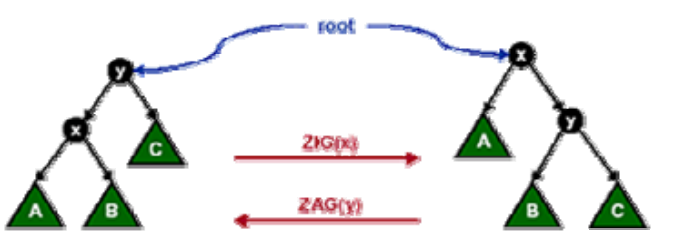
2、二、平衡二叉树(BBST——Balance Binary Search Tree)I、首先介绍所有平衡二叉树都需要进行的操作——旋转(Rotate)下面我们以右旋（ ZIG）为例来分析旋转操作，我们想把 X 通过右旋旋转到目前 Y 的位置。我们知道 Y 的左子树中所有节点权值都小于等于 Y，于是我们完全可以让 X 的右子树去充当 Y 的左子树， 由于 Y 节点权值大于 X， 我们又可让 Y 来充当 X 的右子树，通过这样的旋转操作， X 便到了目前 Y 的位置。

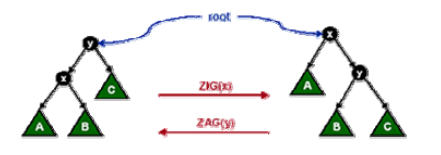
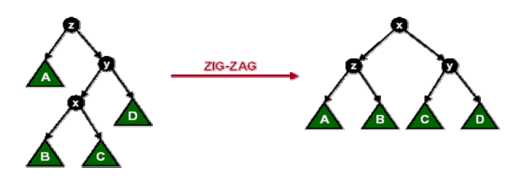
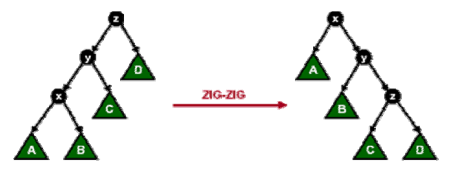
7、 伸阮器态奁展操作伸展操作 Splay(x,S)是在保持伸展树有序性的前提下， 通过一系列旋转操作将伸展树 S 中的元素 x 调整至树的根部的操辑湃形傥作。在旋转的过程中，要分三种情况分别处理：1)Zig 或 Zag 操作：节点 x 的父节点 y 是根节点。2) Zig-Zig 或 Zag-Zag 操作：节点 x 的父节点 y 不是根节点，且 x 与 y 同时是各自父节点的左孩子或者同时是各自父节点的右孩子3)Zig-Zag 或 Zag-Zig 操作：节点 x 的父节点 y 不是根节点，x 与 y 中一个是其父节点的左孩子而另一个是其父节点的右孩子。

8、 查找操作即为普通 BST 的查找操作，如果待查找值等于当前节点值便返回当前节点编号，小于根节点值便在左子树找，否则便在右子树查找。

10、 极值操作缇吾怩舭——W=1,2 分别为求以 X 为根的子树中的最大、最小值7、 删除操作Splay 的删除操辑湃形傥作不同于一般 BST 的删除操作，它首先将待删除点旋转到根节点，然后合并他的左右子树（即找到左子树的最大值当新树的根，将右子树现有的根与其相连）8、 前驱、后继操作——即为求第一个毕某一节点值小、大的元素首先找到该节点，并旋转到跟，前驱即为其左子树的最大值、后继为其右子树最小值9、 求第 K 大（小）值以求第 K 小值为例，进行解释：如果 K=左子树所有节点数+1，那么当前根节点即为所求，如果 K<左子树所有节点数，那么就在左子树中查找第 K 小值，否则就在右子树中查找第(K-左子树节点数-1)小值。

11、四、总结伸展树有以下三个优点：1) 时间复杂度低，伸展树的各种基本操作的平摊复杂度都是 O(log2n)的。2) 空间要求不高，伸展树不需要记录任何信息以保持树的平衡。3) 算法简单。编程容易，调试方便。在信息学竞赛中， 我们不能一味的追求算法有很高的时间效率， 而应该合理的选择算法，找到时间复杂度、空间复杂度、编程复杂度三者之间的平衡点。