表盘上11点到12点的度数问题
1、 1.时针在数字11,分针在数字12,此时时针与分针之间的角(顺时针)是起始角,为330°。

2、2.后续移动的情况为:时针从数字11开始,最终移动数字12;分针的移动范围是从数字12顺时针方向旋转一周,最终回到数字12。
3、3.在分针移动一周360°,共计60个小格时,时针移动5小格,即30°,所以时针走1小格(6°)时候,分针走12小格(72°)。
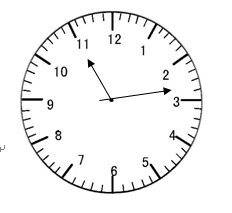
1、 首先找到时针、分钟重合,即成零度的时刻,如图,设此时的时间为:11:x。
在x分钟内:
分针从12走过的角度=x*6°;
时针从11走过的角度=(x/12)*6°.
则此时分针与时针所成的夹角为a:
a= 330°+(x/12)*6°- x*6°
=330°-5.5°x
=0,
此时:x=60分钟,即在12点时候二者重合。
所以:分针与时针所成的角度为
a=330°+(x/12)*6°- x*6°
=330°-5.5°x。
1、1.a=0°的时候:12点整;
2.a=30°的时候:
330°-5.5°x=30°,得到x=600/11分,即11点600/11分,成30°。
3.a=45°的时候:
330°-5.5°x=45°,得到x=570/11分,即11点570/11分,成45°。
2、4. a=60°的时候:
330°-5.5°x=60°,得到x=540/11分,即11点540/11分,成60°。
5. a=90°的时候:
330°-5.5°x=90°,得到x=480/11分,即11点480/11分,成90°。
6. a=120°的时候:
330°-5.5°x=120°,得到x=420/11分,即11点420/11分,成120°。
3、7. a=150°的时候:
330°-5.5°x=150°,得到x=360/11分,即11点360/11分,成150°。
8. a=180°的时候:
330°-5.5°x=180°,得到x=300/11分,即11点300/11分,成180°。
9. a=240°的时候:
330°-5.5°x=240°,得到x=180/11分,即11点180/11分,成240°。
10. a=300°的时候:
330°-5.5°x=300°,得到x=60/11分,即11点60/11分,成300°。
1、 (1)11:10,
a=|5.5°x-330°|=|5.5°*10-330°|
=|55°-330°|=275°;

2、(2)11:15,
a=|5.5°x-330°|=|5.5°*15-330°|
=|82.5°-330°|=247.5°;

3、(3)11:20,
a=|5.5°x-330°|=|5.5°*20-330°|
=|110°-330°|=220°;

4、 (4)11:25,
a=|5.5°x-330°|=|5.5°*25-330°|
=|137.5°-330°|=192.5°;

5、 (5)11:30,
a=|5.5°x-330°|=|5.5°*30-330°|
=|165°-330°|=165°;

6、(6)11:35,
a=|5.5°x-330°|=|5.5°*35-330°|
=|192.5°-330°|=137.5°;

7、(7)11:40,
a=|5.5°x-330°|=|5.5°*40-330°|
=|220°-330°|=110°;

8、 (8)11:45,
a=|5.5°x-330°|=|5.5°*45-330°|
=|247.5°-330°|=82.5°;

9、(9)11:50,
a=|5.5°x-330°|=|5.5°*50-330°|
=|275°-330°|=55°;

10、(10)11:55,
a=|5.5°x-330°|=|5.5°*55-330|°
=|302.5°-330°|=27.5°。
