【抽象代数】用Mathematica求代数数本原多项式
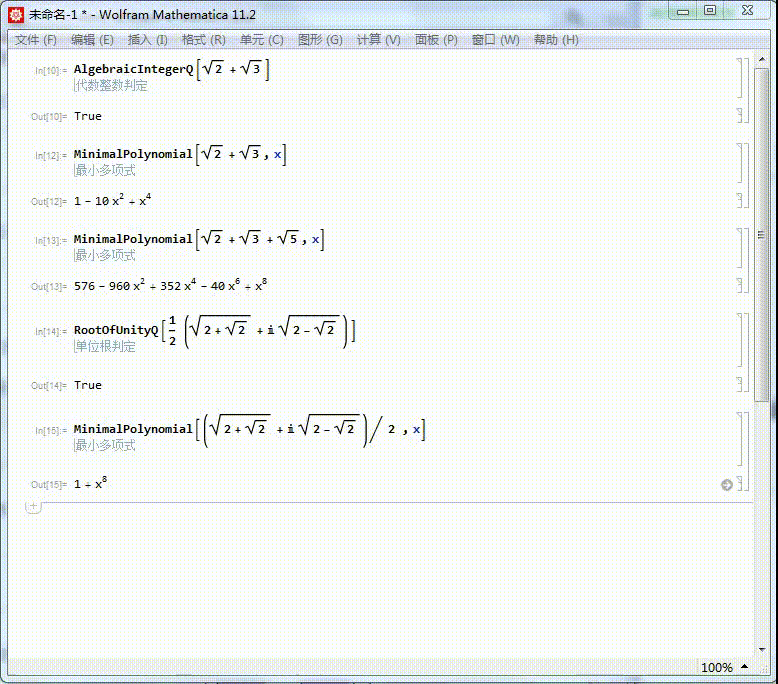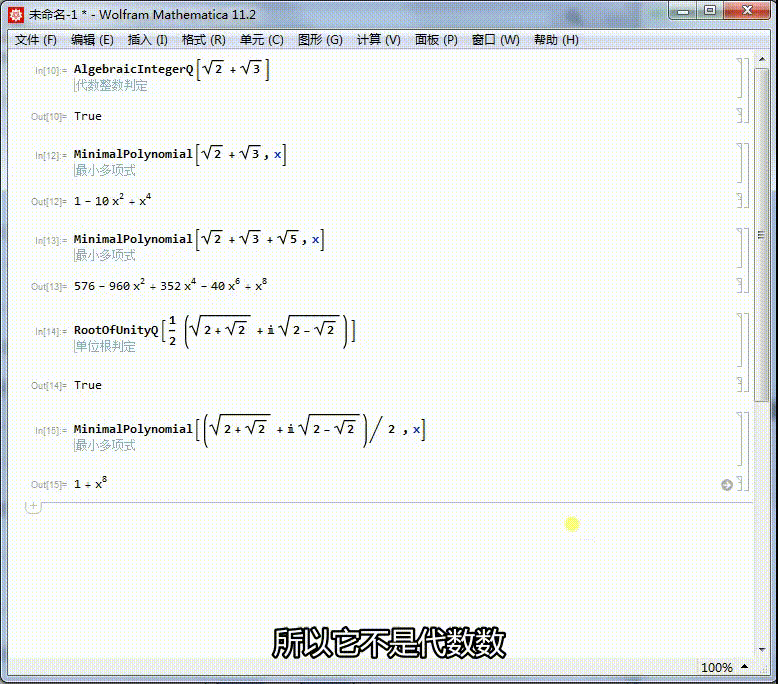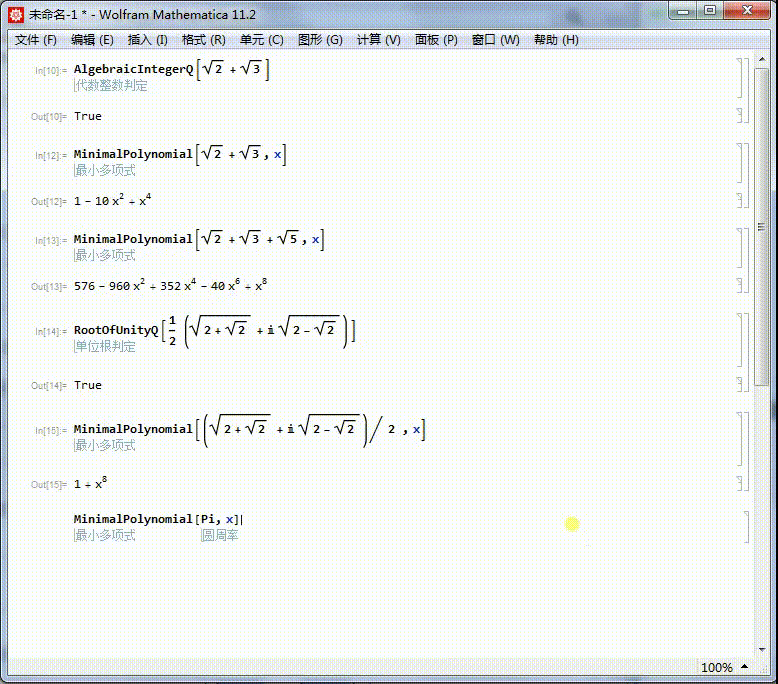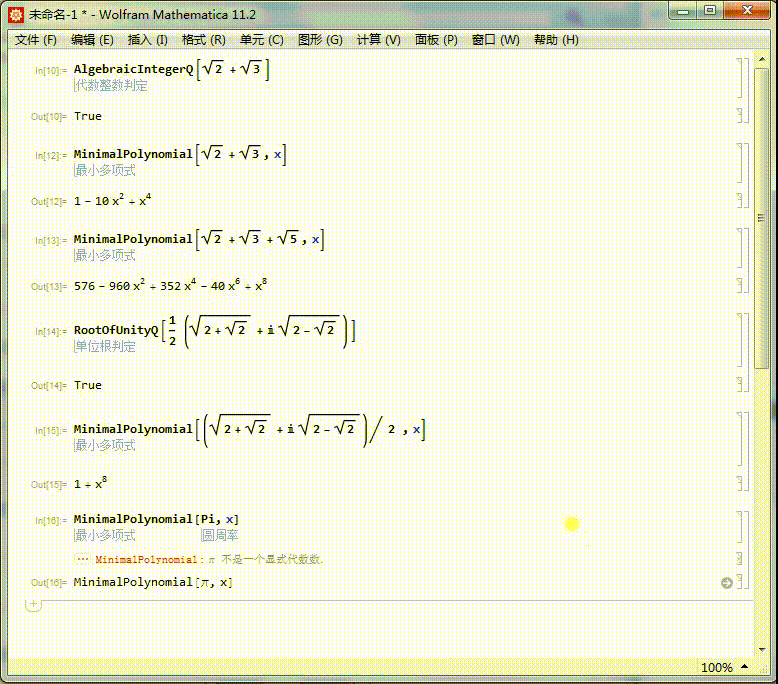
1、我们知道Sqrt[2] + Sqrt[3] 是代数整数,它的本原多项式是:
MinimalPolynomial[Sqrt[2] + Sqrt[3]]
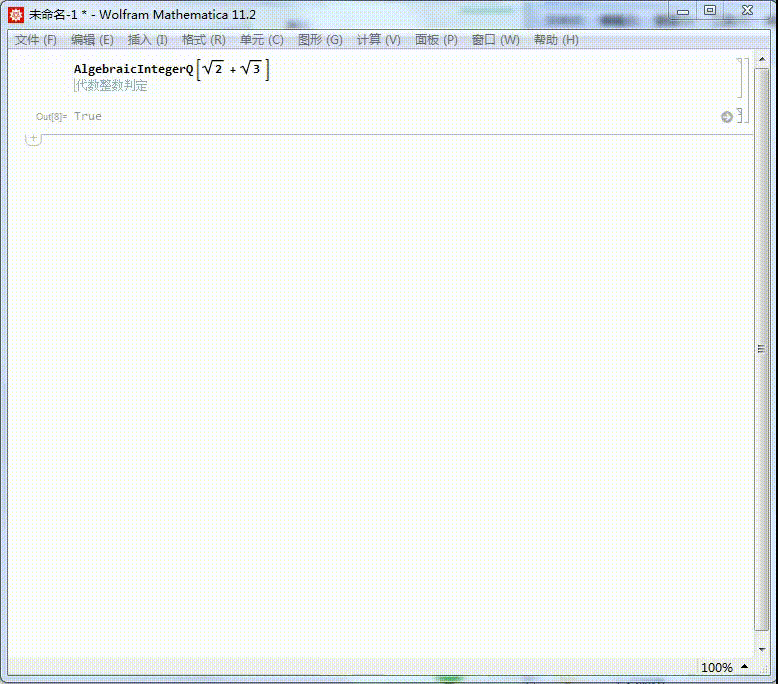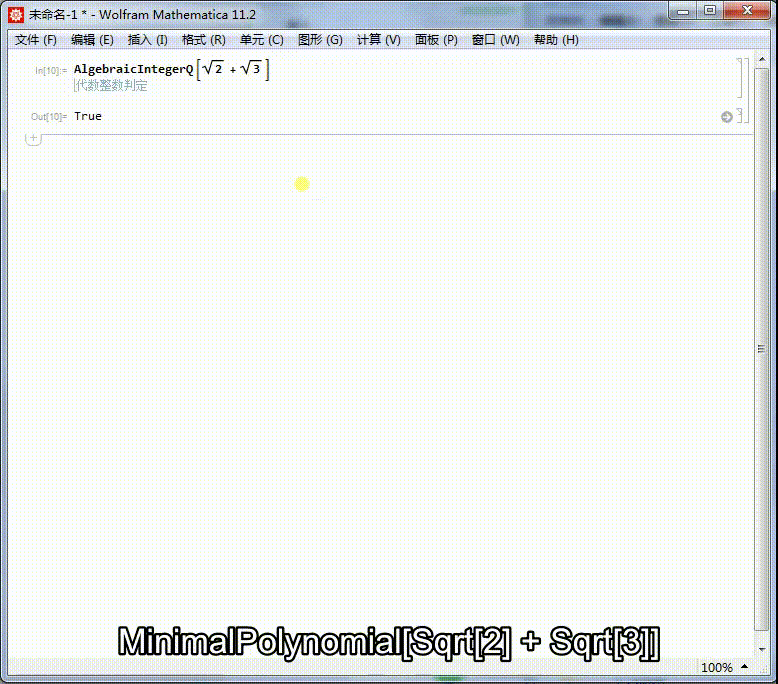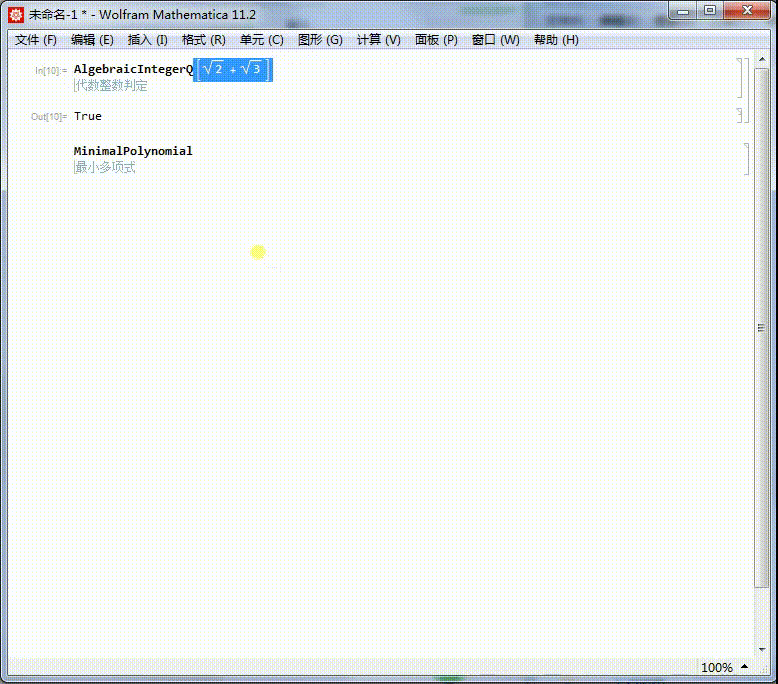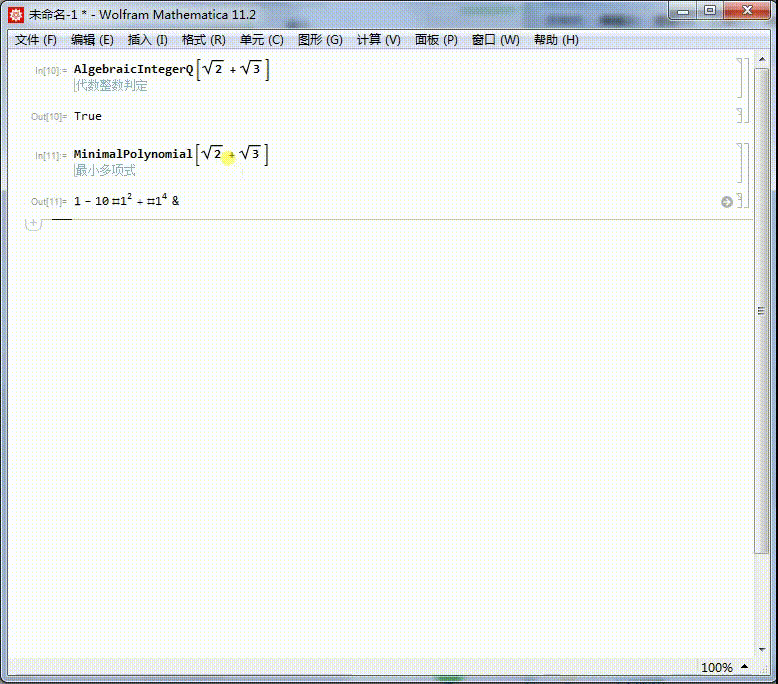
2、上面返回的是一个纯函数。如果需要一个关于x的多项式,可以写为:
MinimalPolynomial[Sqrt[2] + Sqrt[3],x]

3、同样的,Sqrt[2] + Sqrt[3] + Sqrt[5]的本原多项式也可以求出来,结果得到的多项式有点复杂:
MinimalPolynomial[Sqrt[2] + Sqrt[3] + Sqrt[5],x]

4、(Sqrt[2+Sqrt[2]]+I Sqrt[2-Sqrt[2]])/2是一个单位根:
RootOfUnityQ[(Sqrt[2 + Sqrt[2]] + I Sqrt[2 - Sqrt[2]])/2]

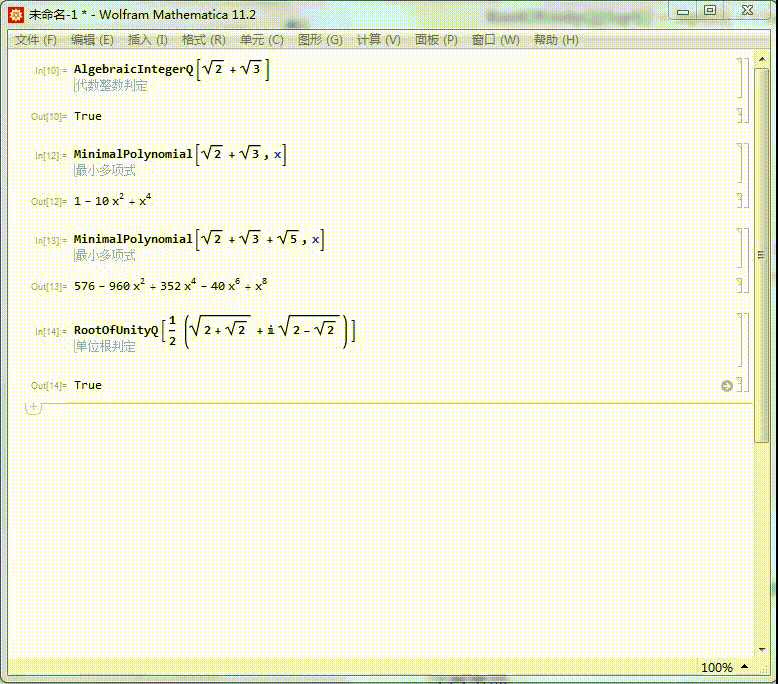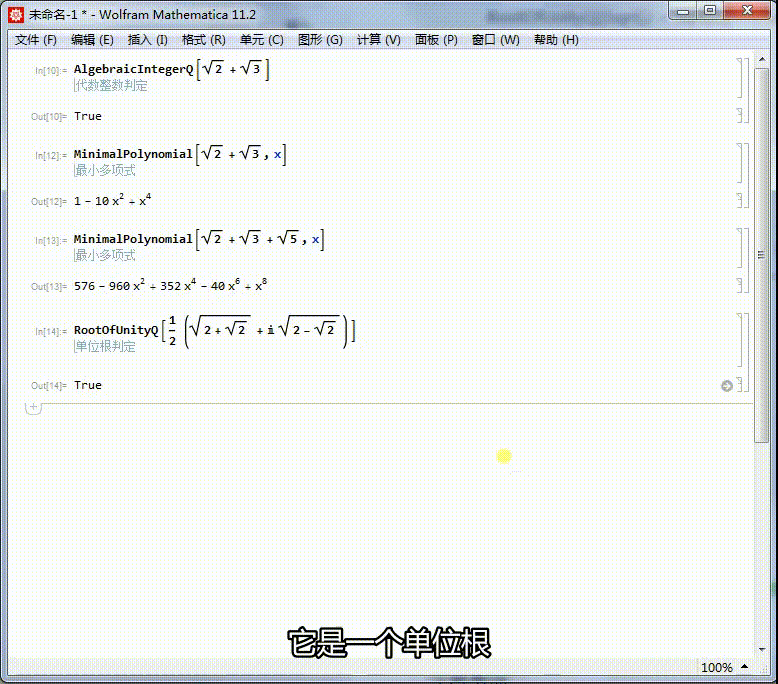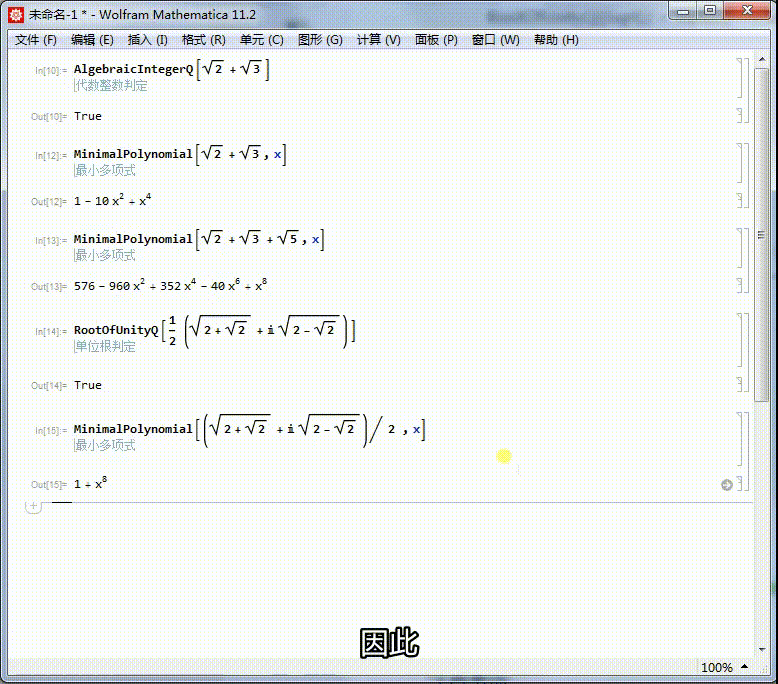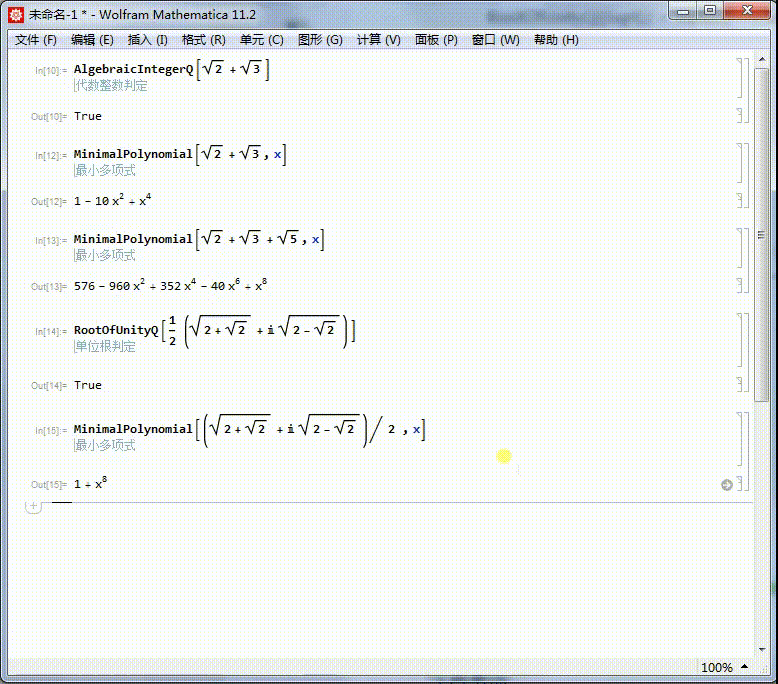
5、求出它的本原多项式,可以进一步证明,它是一个单位根。
它的本原方程是x^8+1=0,因此,它是一个16次单位根。
6、圆周率不存在本原多项式,所以它不是代数数。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:121
阅读量:141
阅读量:114
阅读量:114
阅读量:96