【射影几何】怎么用配极变换解决平面几何问题

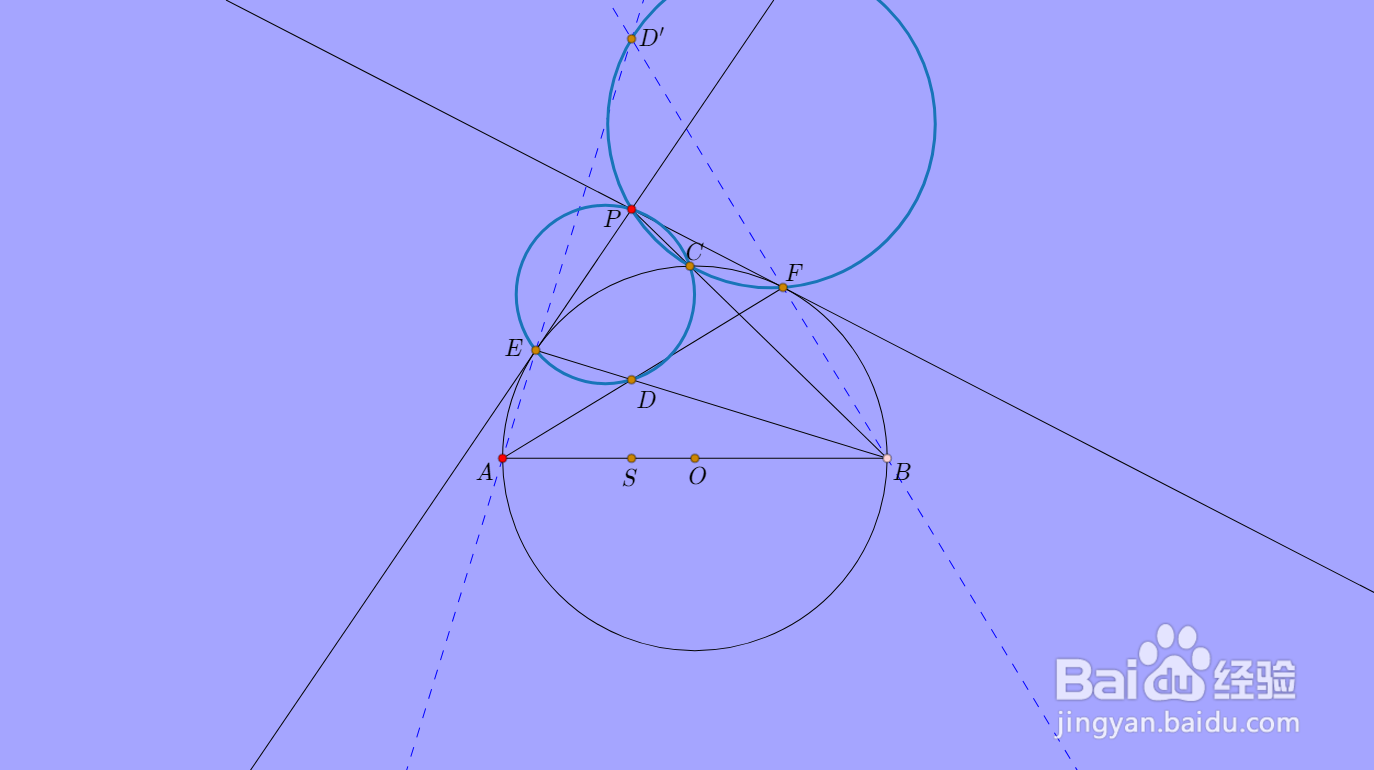
1、为了便于作图，用网络画板。题图如下：

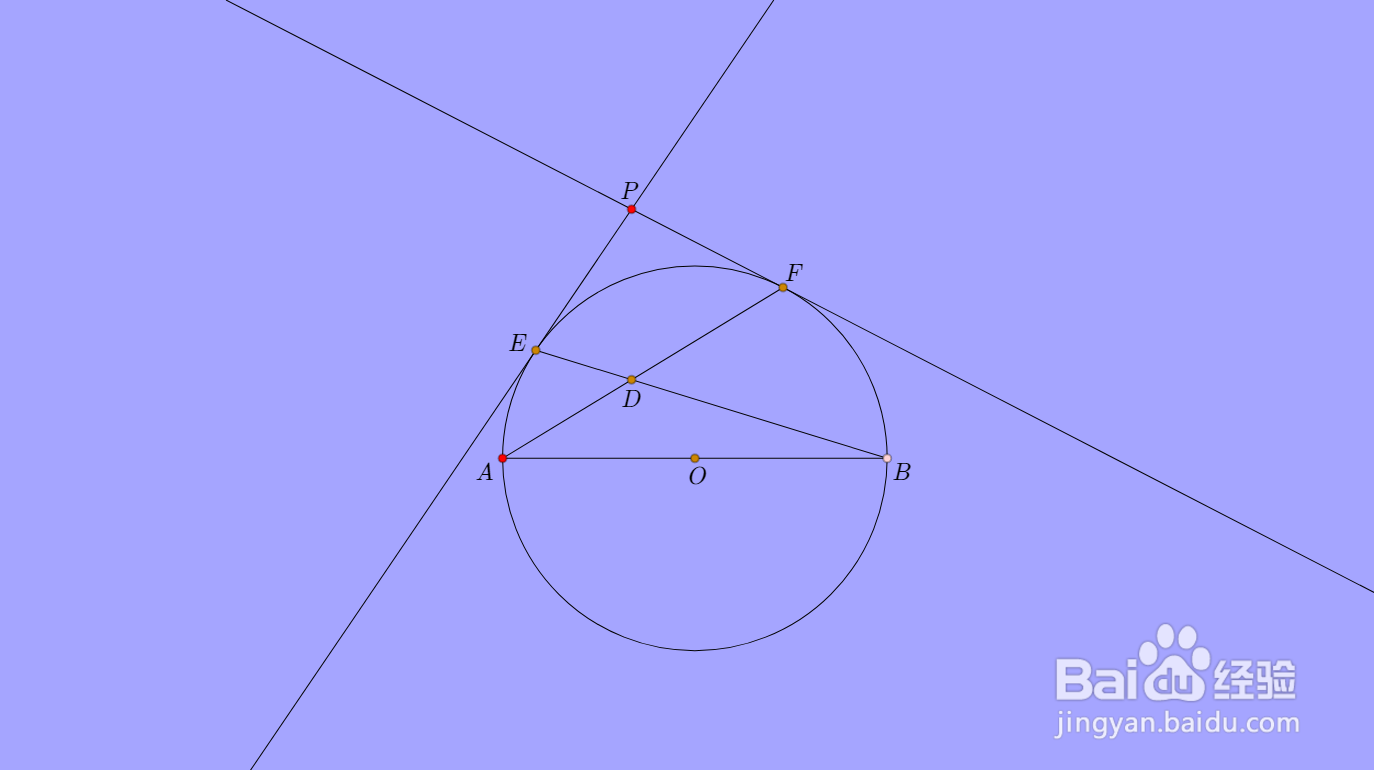
2、设直线AE和BF交于D'，那么容易发现D是三角形ABD'的垂心。

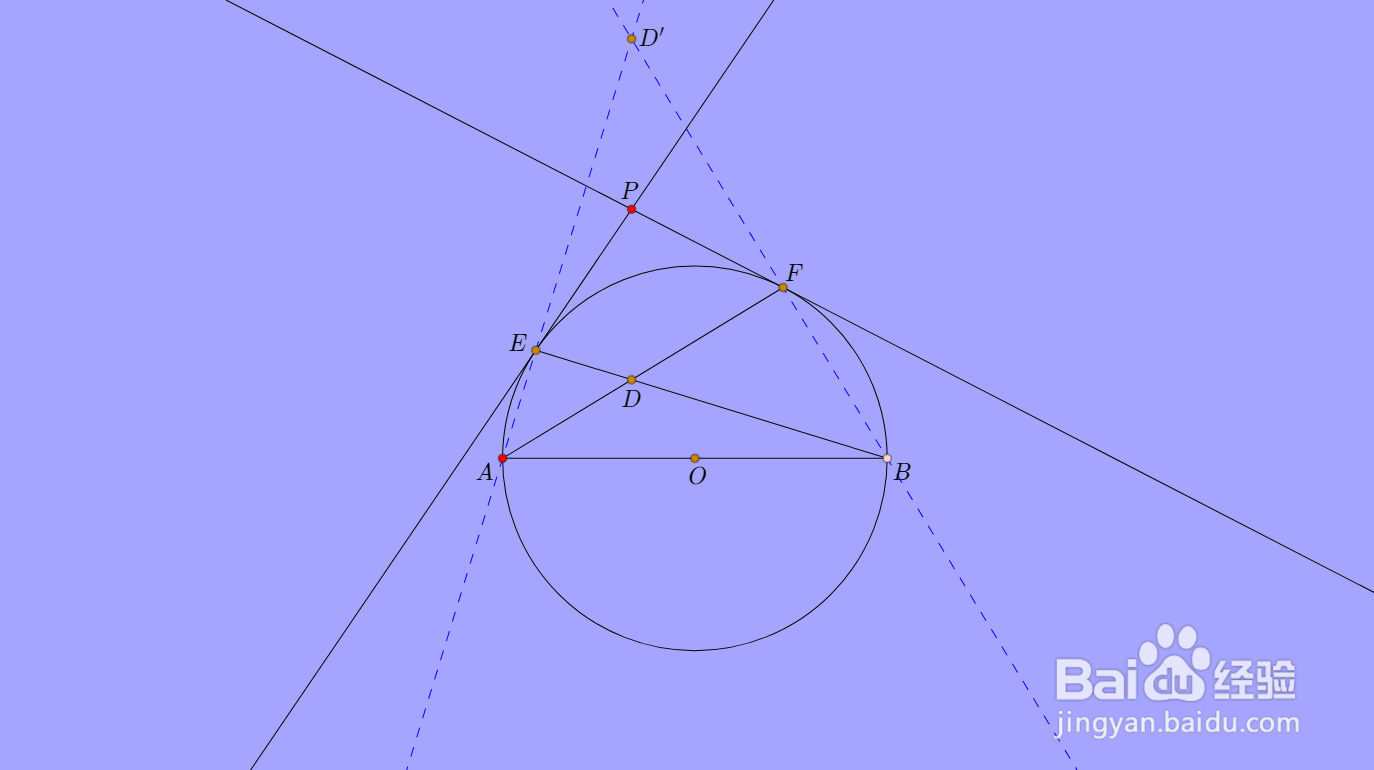
3、考虑D关于圆O的极线，是什么。D的极线必定经过D'点，另一个点则是AB和EF的交点U。那么直线UD'就是D的极线。

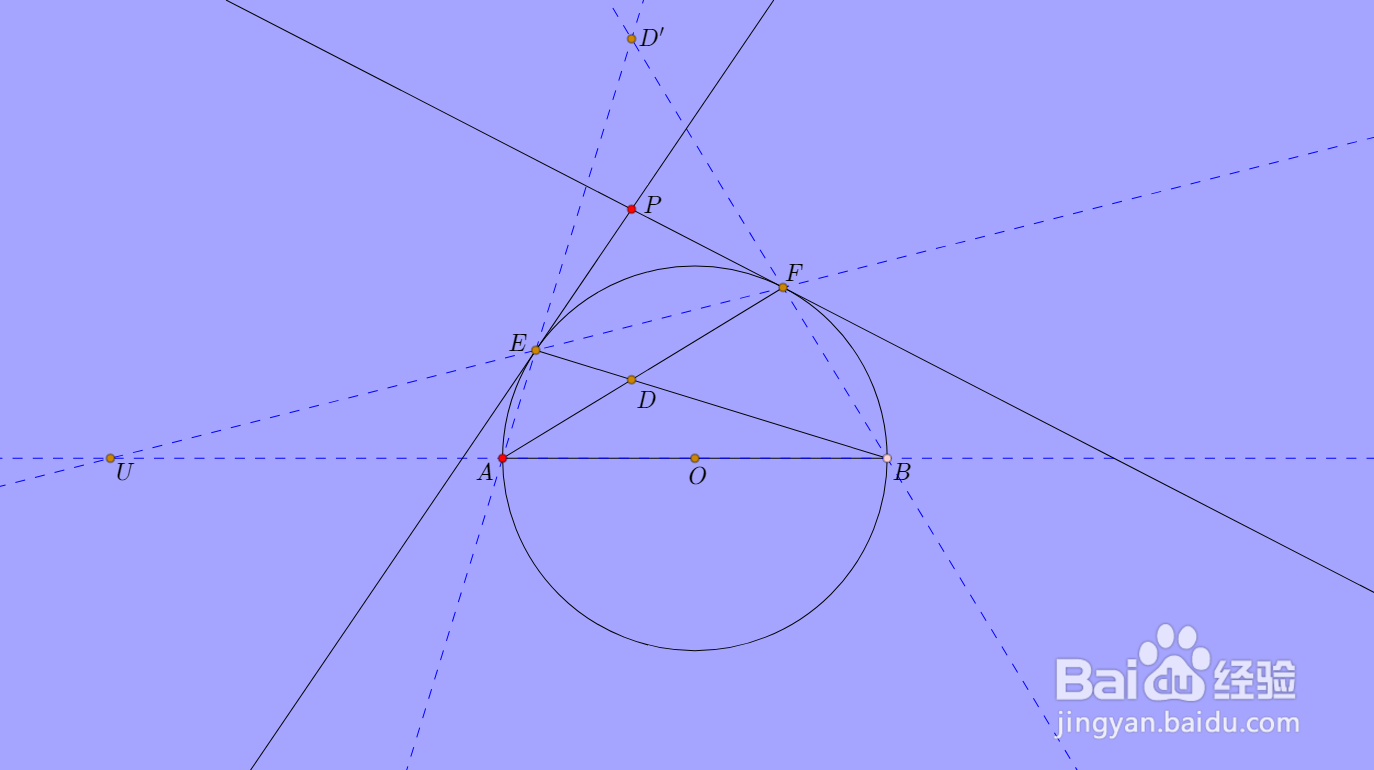
4、UDD'实际上是自极三点形：D的极线，是直线UD'；D'的极线，是直线UD；U的极线，是直线DD'。

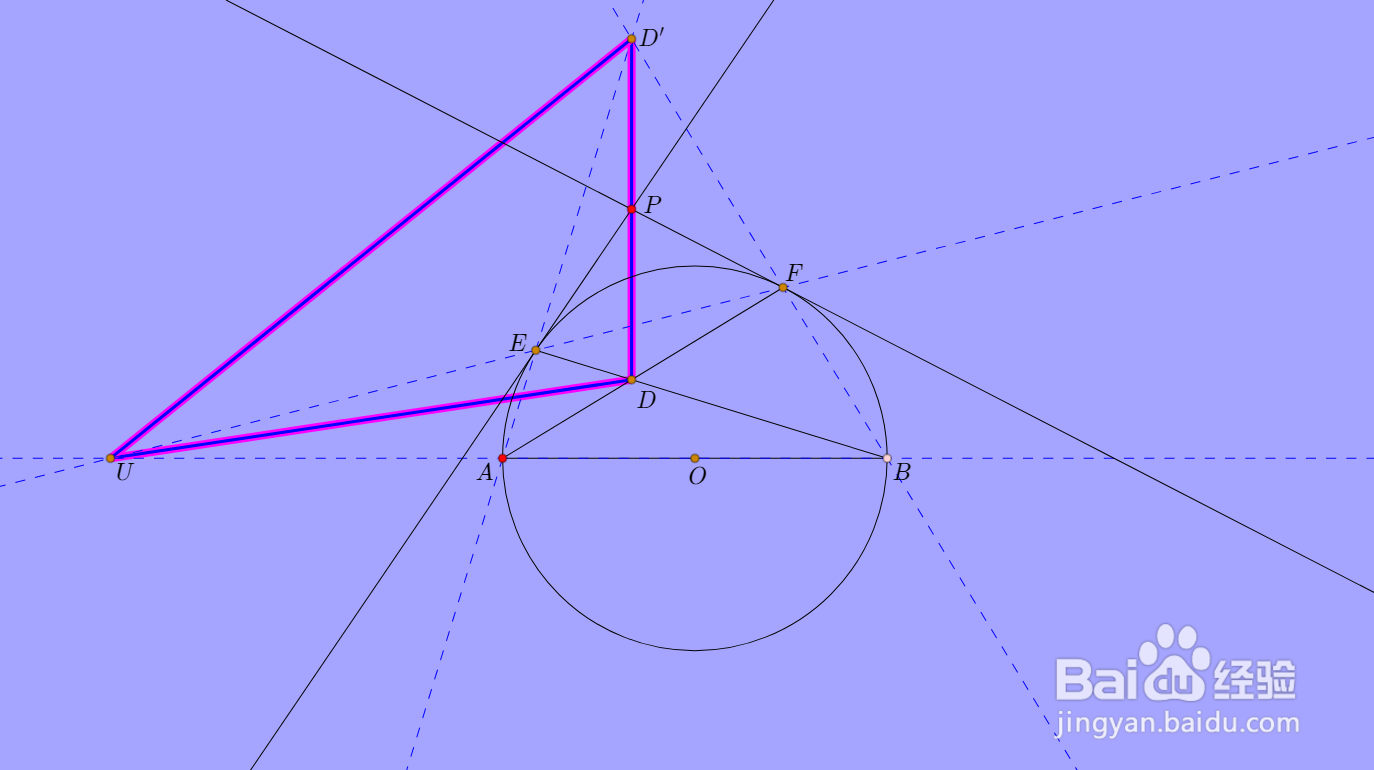
5、U、E、F三点共线，它们的极线也得共点，即DD'、PE、PF三线共点，这个点就是点P。也就是说，DD'P共线。进而说明，PD垂直于AB。

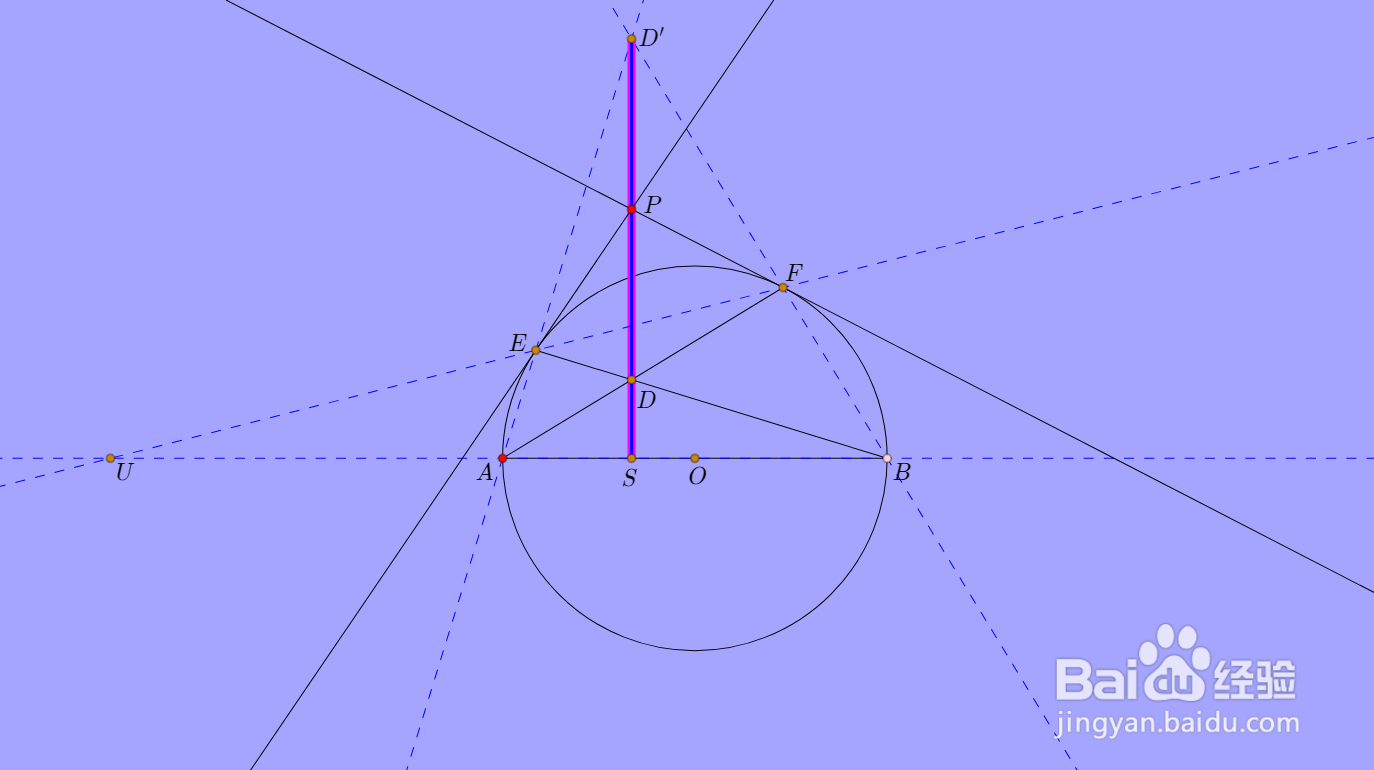
6、垂足记为点S，则：∠PDF=∠ADS=∠ABF=∠AFP，所以PD=PF。

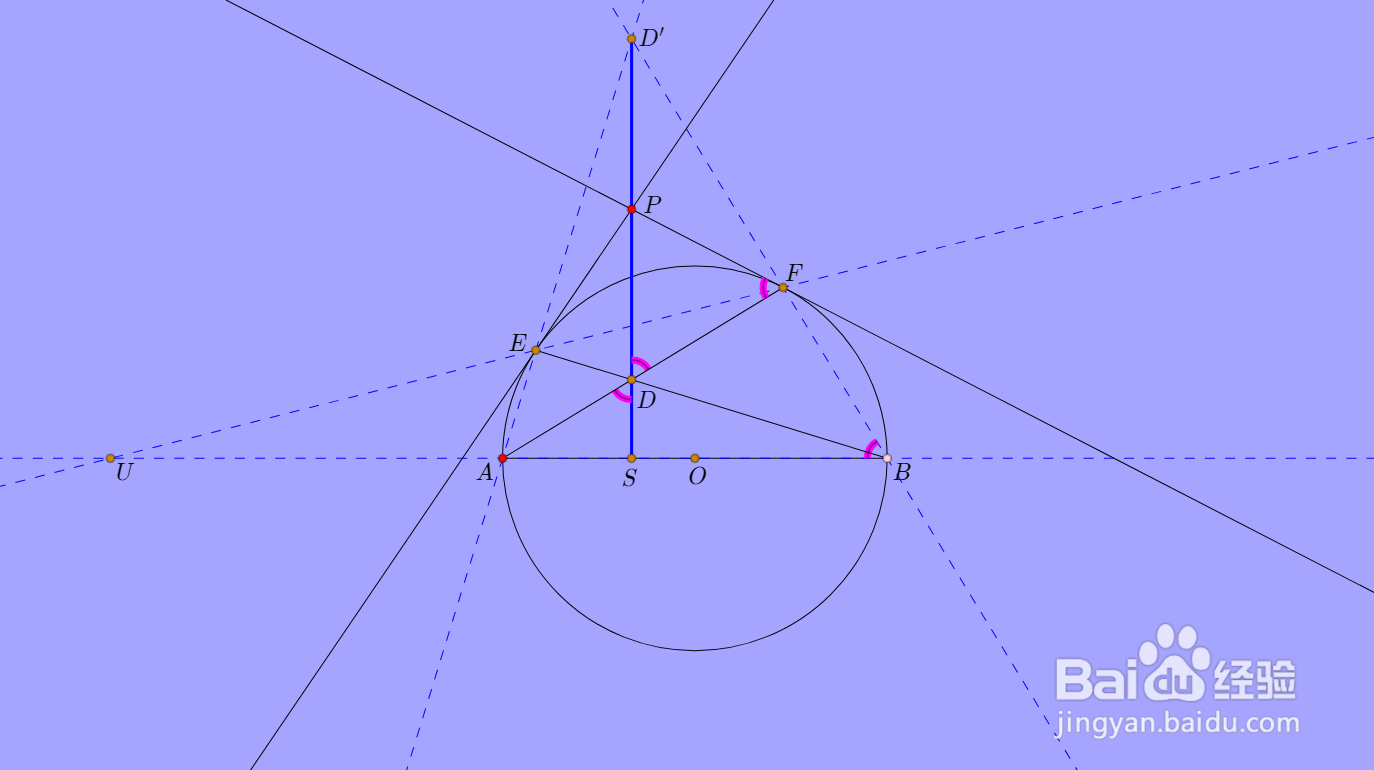
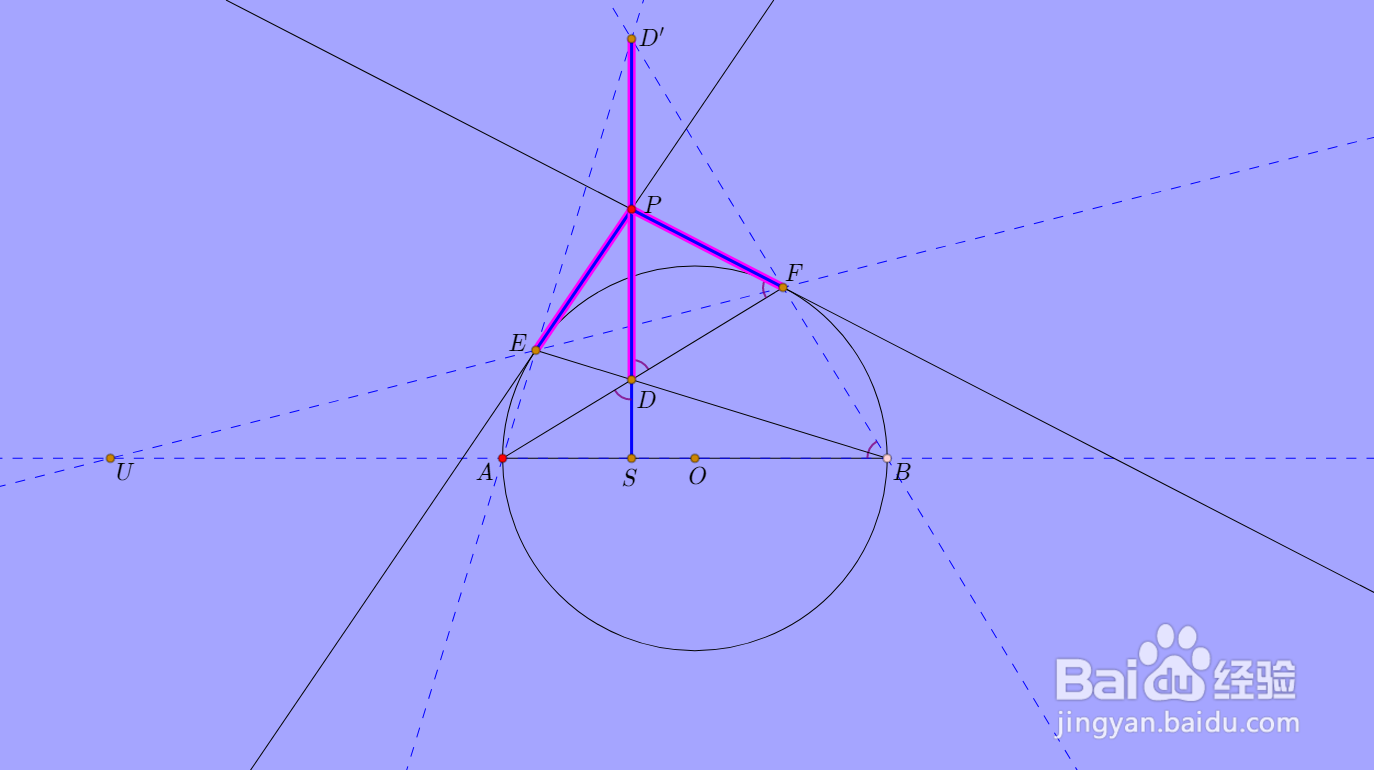
7、这样就证明了PD=PE=PF的结论。实际上，P是线段DD'的中点。

8、还可以进一步证明，PCDE四点共圆。

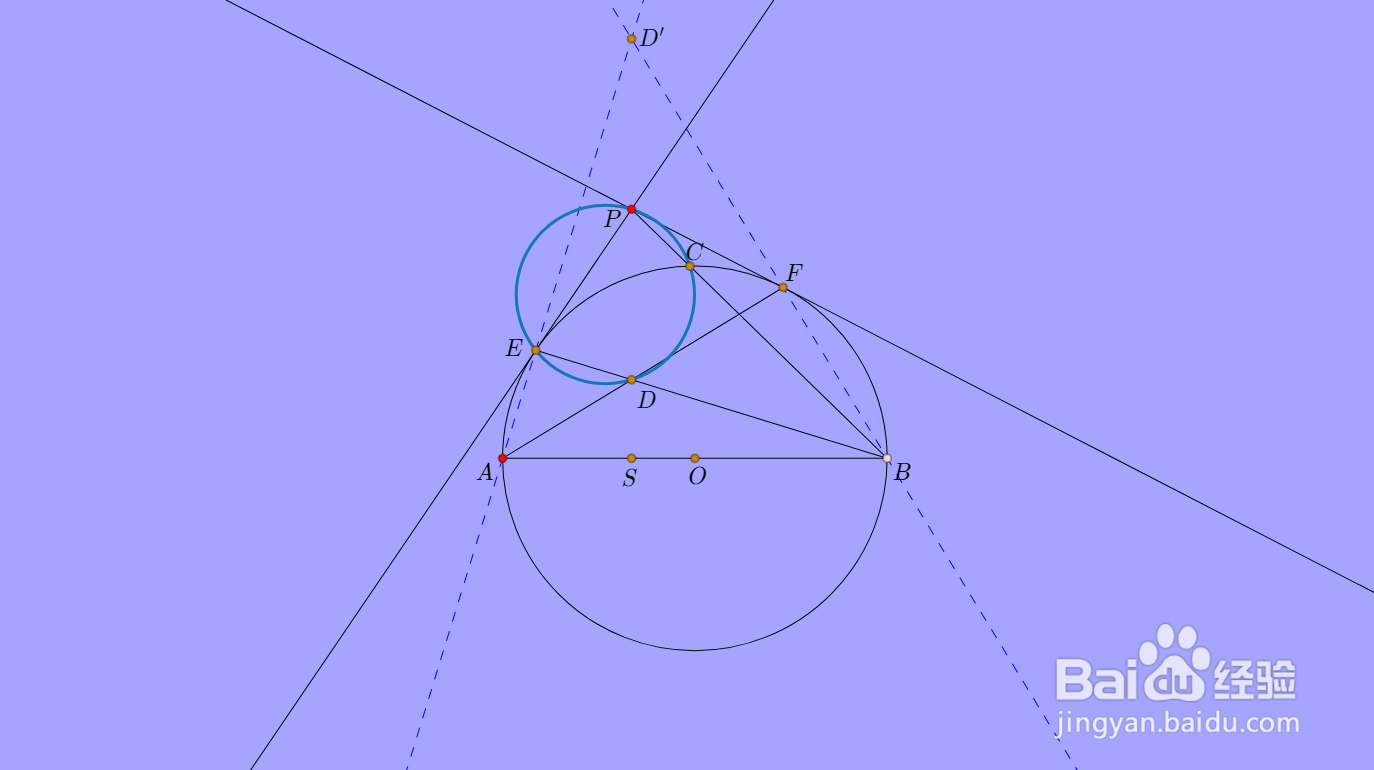
9、类似的，还有PCFD'四点共圆。