初中数学中如何通过特殊点来解题？

1、特殊点，不单单是点，还包括线、图形等。找到特殊点能给解题带来柳暗花明的感觉。

引入:在三角形ABC中有一个内角是36°，过顶点A做直线AD，将其分为两个等腰三角形。则满足上述条件的三角形ABC共有几个？

2、首先确定第一个特殊点。

第一个特殊点就是哪一个内角是36°？

∠A=36°？∠B=36°？∠C=36°？

这样就出现了三种不同的情形，需要进一步的演算。

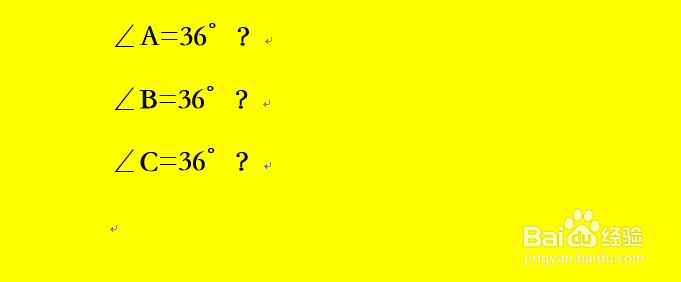
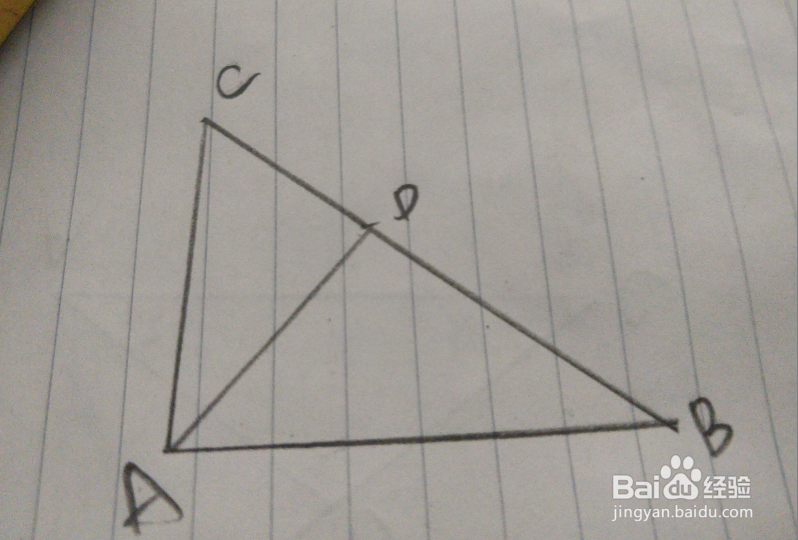
3、然后确定第二个特殊点。

第二个特殊点就是等腰三角形的哪两条边是腰？

三角形ABD中：BD=AD？AD=AB？

三角形ACD中：CD=AD？AD=AC？

这样就会出现四种不同的情况。

4、接着根据第一个特殊点进行展开。

题目尚未明确哪个内角是36°。所以呢，要分三种情况来分析。

第一种情况：∠A=36°；

第二种情况：∠B=36°；

第三种情况：∠C=36°。

5、当∠A=36°时，

假设∠B为锐角时，

∠DAB=∠B，∠CDA=∠CAD=2∠B，得∠A=3∠B，所以∠B=12°，∠C=132°。

6、假设∠B为钝角时，

同理可得，∠C=12°，∠B=132°。

不论∠B是锐角还是钝角，这两个三角形是全等的，算是一种三角形。

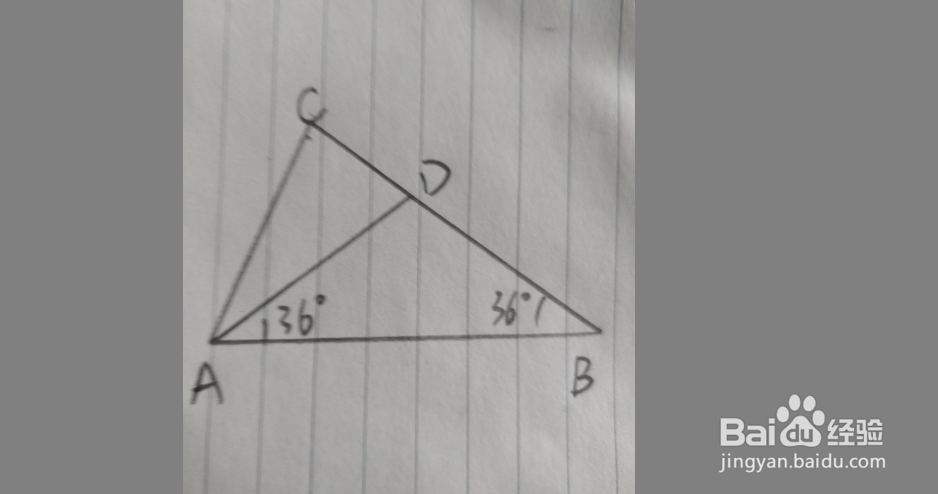
7、当∠B=36°时，

此时需要对第二个特殊点进行展开。

若AC=AD=BD，则∠C=∠CDA=72°，∠A=72°

8、若CD=AD=BD，则∠C=（180°-36°*2）/2=54°，∠A=90°

9、若AD=BD，AC=CD，

则∠A=∠BAD+∠CAD=36°+72°=108°，

∠C=180°-72°-72°=36°

10、若AD=AB时，∠ADB=36°，

∠CDA=180°-36°=144°，

∠C=∠DAC=（180°-144°）/2=18°，

∠A=126°

11、当∠C=36°时，

情况与∠B=36°时是一样的。

故符合题设的有五个不同的形状。