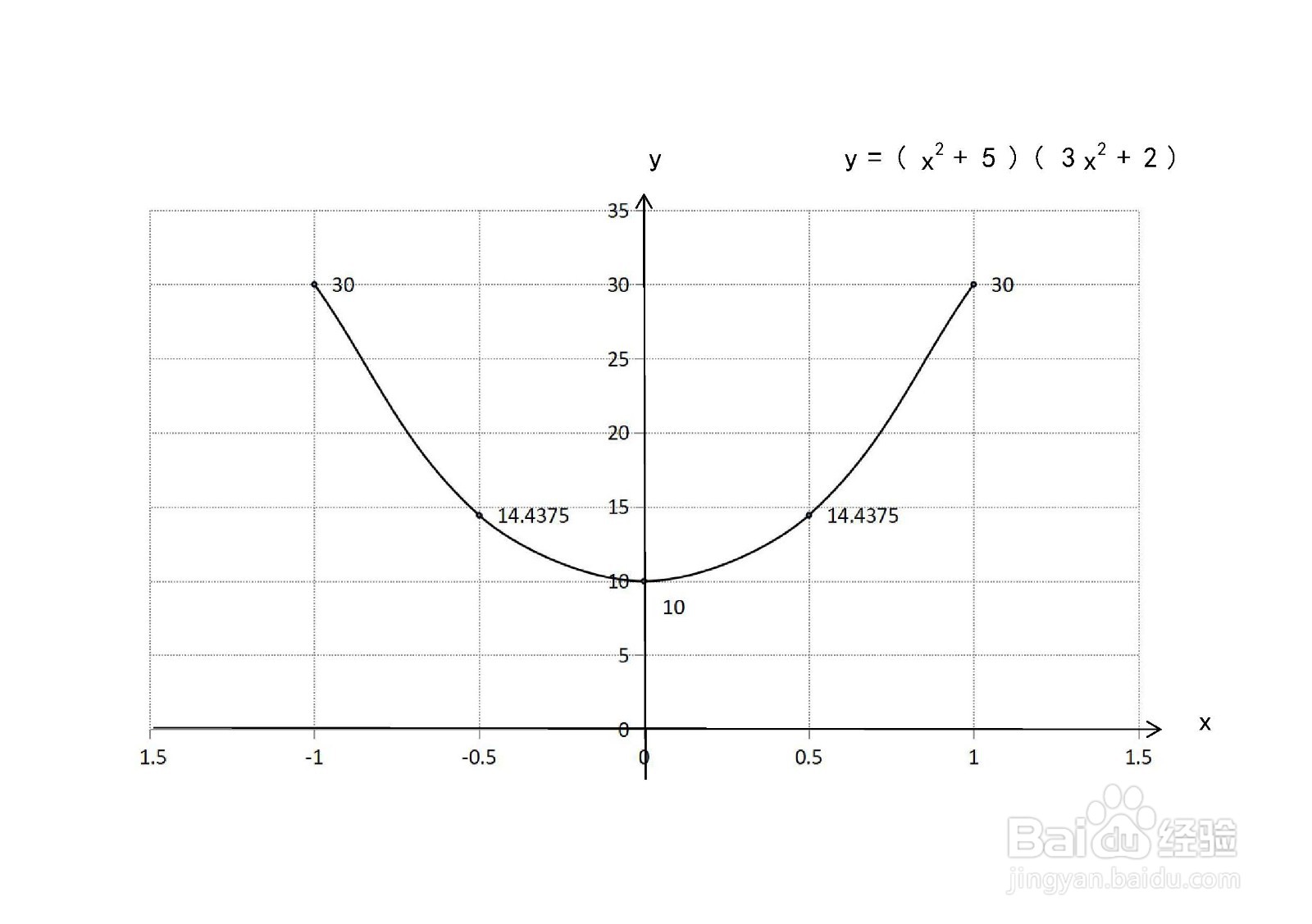
导数画两个偶函数乘积y=(x^2+5)(3x^2+2)图像

1、根据函数特征，自变量是二次函数乘积形式，函数自变量可以取全体实数，即定义域为(-∞，+∞）。

2、求出函数的一阶导数，令一阶导数为0，求出函数的驻点，再根据函数的驻点判断导数的符号，即可得函数的单调性，进而得函数的单调区间。

3、本题求一阶导数的主要过程和步骤为：

y=(x^2+5)(3x^2+2)

y'=2x(3x^2+2)+(x^2+5)*6x

=2x(3x^2+2+3x^2+15）

=2x(6x^2+17)

即可得到驻点为x=0。

4、如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加;反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。

5、二阶导数，是原函数导数的导数，将原函数进行二次求导。一般的，函数y=f(x)的导数y'=f'(x)仍然是x的函数，则y'=f'(x)的导数叫做函数y=f(x)的二阶导数。

6、通过函数的二阶导数，求出函数的拐点，再根据拐点判断二阶导数的符号，即可解析函数的凸凹性，进一步即得函数的凸凹区间,本题二阶导数的计算过程如下：

y'=2x(6x^2+17).

y''=2(6x^2+17)+2x*12x

=2(6x^2+17+12x^2)

=2(18x^2+17)>0,

函数为凹函数。

7、函数的极限，判断函数在端点处的极限及函数的极值。

8、根据函数奇偶性判断方法，本经验中可以得到f(-x)=f(x),判断函数为偶函数。

f(x)=(x^2+5)(3x^2+2),

则：f(-x)

=[(-x)^2+5][3(-x)^2+2]

=(x^2+5)(x^2+2).

=f(x),即函数为偶函数。

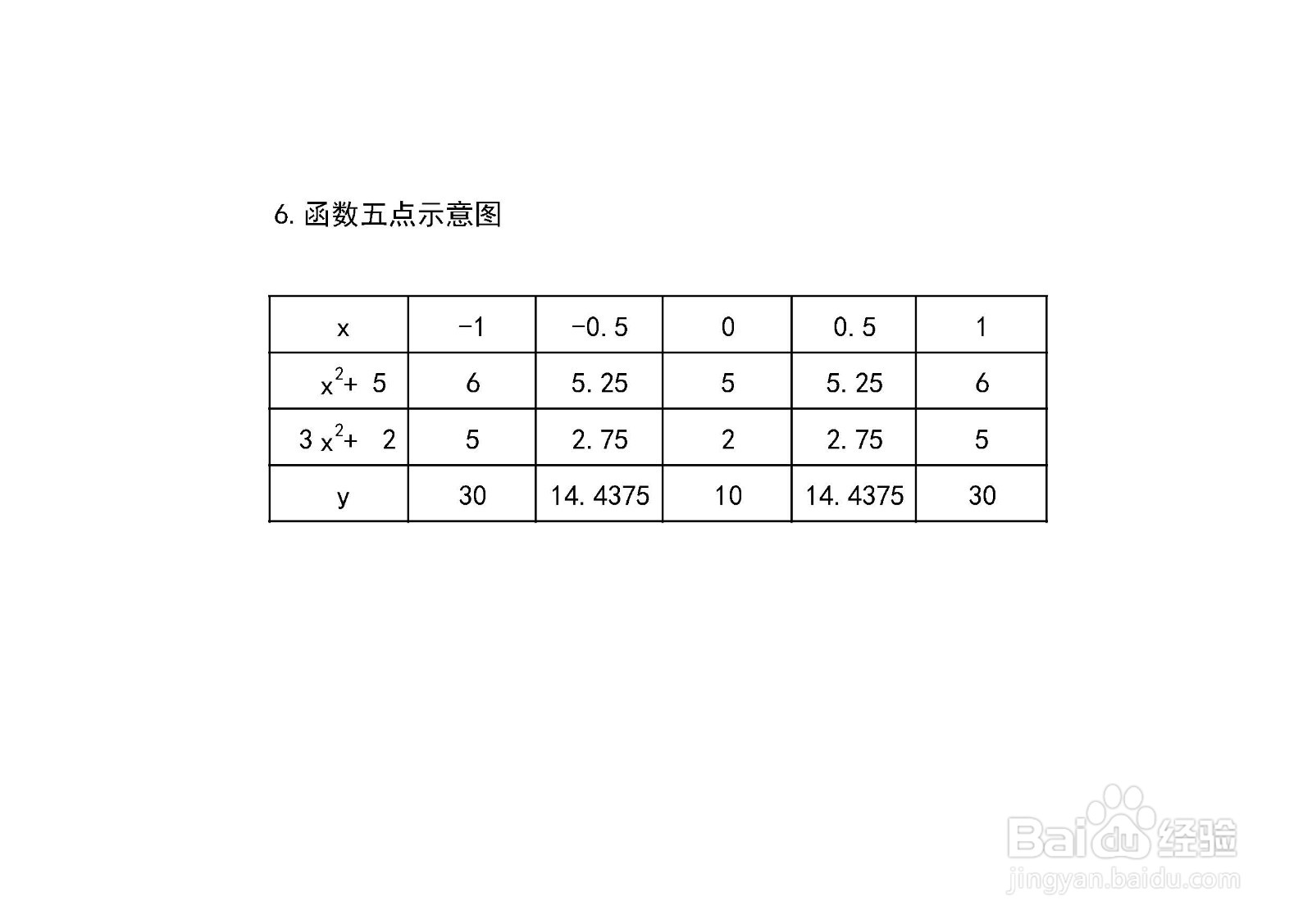
9、函数部分点解析表如下：

例如：当x=0时，y=(0+5)(0+2)=10；

当x=1时，y=(1^2+5)(3*1^2+2)=6*5=30；

当x=-1时，y=[(-1)^2+5][3*(-1)^2+2]=6*5=30.

10、根据函数的定义域、单调性、凸凹性、极限、奇偶性等性质，函数的示意图如下：