极值点偏移的基本解题方法?
1、极值点偏移问题的证明方法,第一种是函数的单调性,第二种是利用对数平均不等式证明。

2、首先我们需要两个正数a和b,算出他两个的平均数、集合平均数的大小关系,然后证明。

3、加下来需要分析构造对称函数、构造比较函数。

4、它总共有五种解决方法,一其次构造消参,二利用极值点偏移构造函数处理,三构造函数,四引入变量,五巧引入变量。
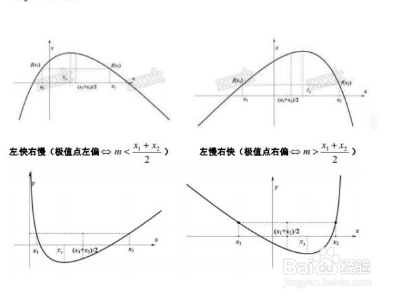
1、1、极值点偏移有两种证明方法。
2、需要分析构造对称函数、构造比较函数。
3、它总共有五种解决方法。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:97
阅读量:162
阅读量:118
阅读量:115
阅读量:54