sin1/x是有界函数吗

sin1/x是有界函数。

证明如下：

考虑x趋近于绣诅收蟮无穷时，1/x趋近于0，sin(1/x)趋近于0。

考虑x趋近于0，1/x趋近于无穷，sin(1/x)为周期函数，值域为[-1,1]，最小正周期为1/2pi。

以上，有界。

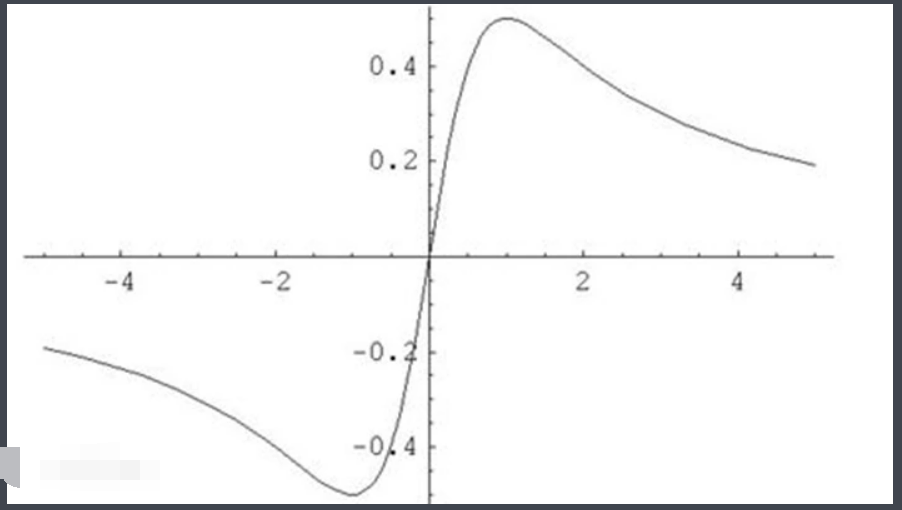
相关概念

设函数f(x)是某一个实数集A上有定义，如果存在正数M 对于一切X∈A都有不等式|f(x)|≤M的则称函数f(x)在A上有界，如果不存在这样定义的正数M则称函数f(x)在A上无界 设f为定义在D上的函数，若存在数M（L），使得对每一个x∈D有： ƒ(x)≤M（ƒ(x)≥L）。

则称ƒ在D上有上（下）界的函数，M（L）称为ƒ在D上的一个上（下）界。