【微分几何】椭球面怎么进行Gauss变换？

1、椭球面的参数方程可以是？贪块：

r[{u_, v_}] := {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}*{3, 4, 5}

.

这个椭球面没有焦点了。

2、Gauss变换的过程：

ru = D[r[{u, v}], u];

rv = D[r[{u, v}], v];

计算法向量：

uv = Cross[ru, rv];

把法向量化为单位向量：

uv/Sqrt[uv.uv]

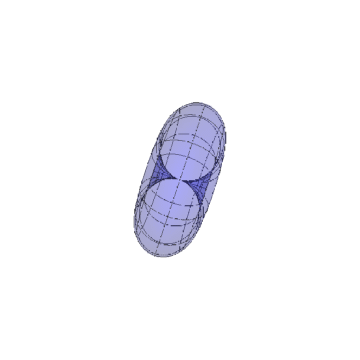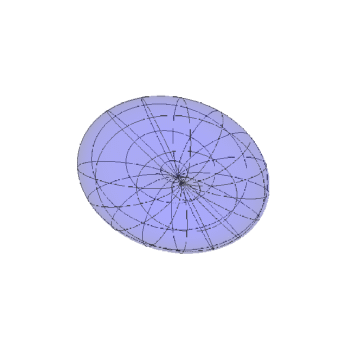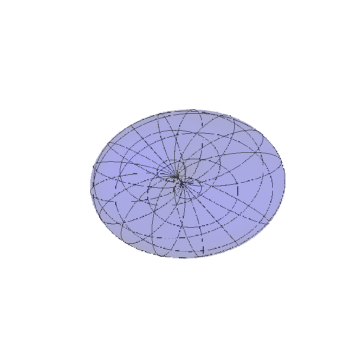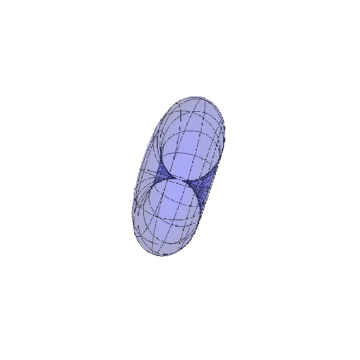
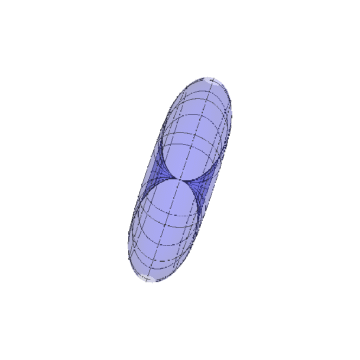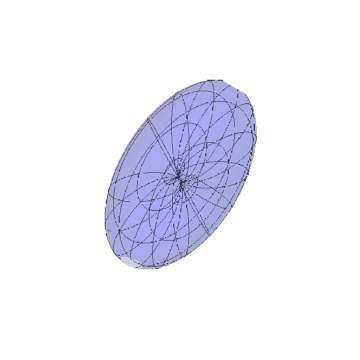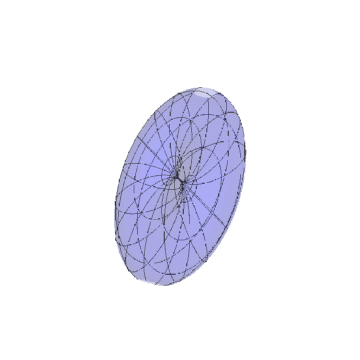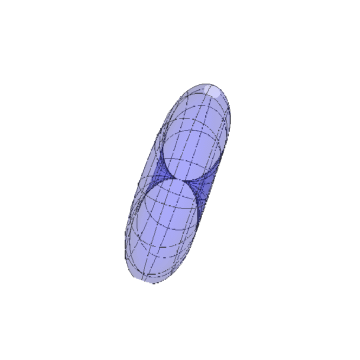
把归一化的法向量视为新区面的参数方瞧扯速程，得到一个类似于球面的曲面。

.

这个"球面"中间有一称茄个空腔？

3、如果直接把向量uv视为新区面的参数方程，得到的曲面如下。

可以看到，中间真的存在凹陷。

4、椭球面：

{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}*{3, 3, 5}

5、椭球面：

{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}*{5, 3, 5}