【抽象代数】不定方程x^3-1=2y^3的解法
1、在《【抽象代数】虚二次Euclid域》里面,我们证明了,Q[sqrt(-2)]是一个Euclid域,因此Q[sqrt(-2)]的代数整数环是唯一因子分解整环。
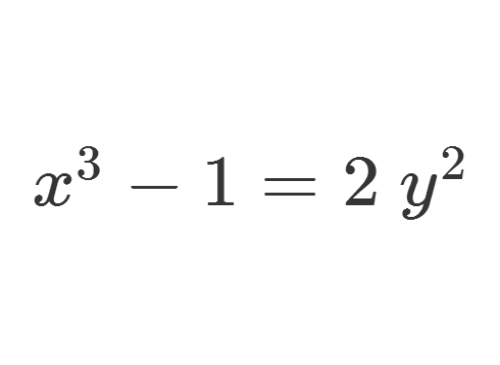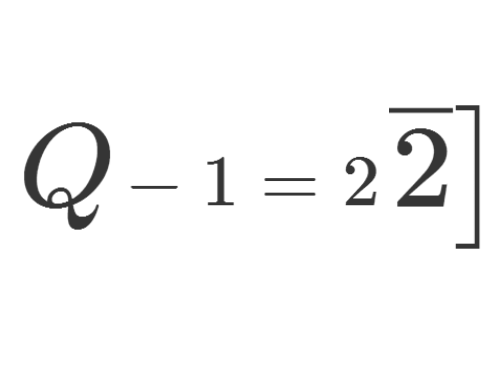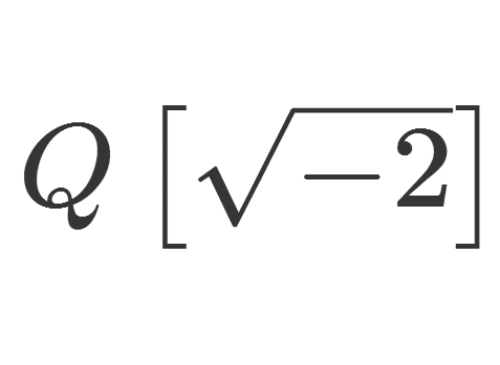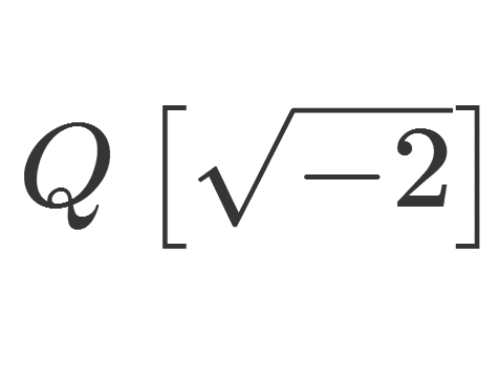
2、关于y的项的次数是2,且Q[sqrt(-2)]里面的代数整数环是唯一因子分解整环,所以我们要在Z[sqrt(-2)]里面,考察给定的不定方程。

3、假设上式右边两个分解式的最大公约数为δ,那么δ可以为1或sqrt(-2)。
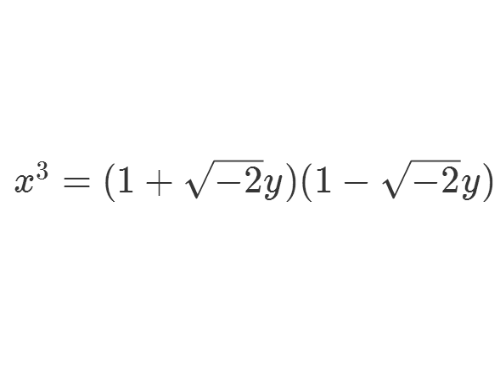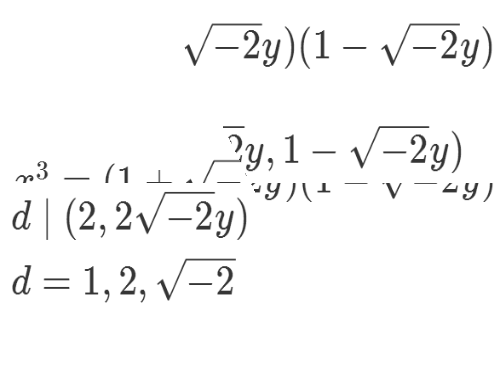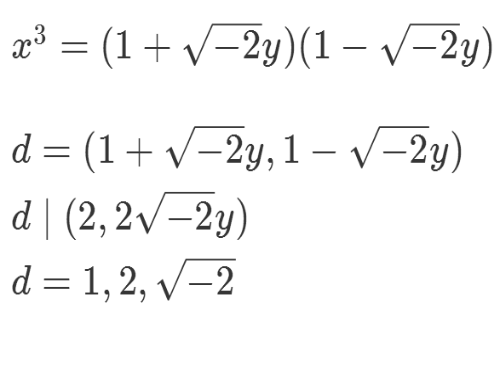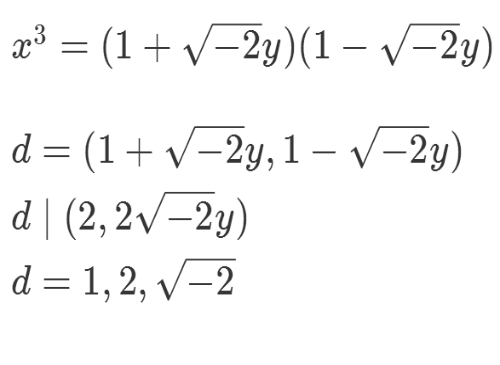
4、稍作分析,就可以证明,d只能等于1。
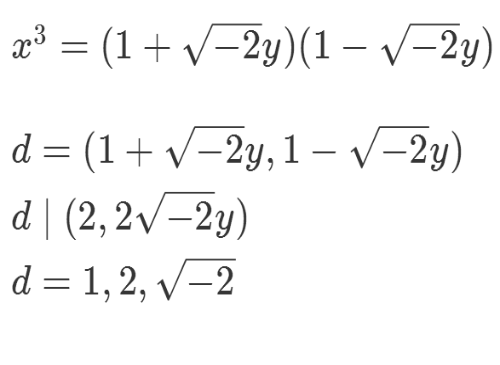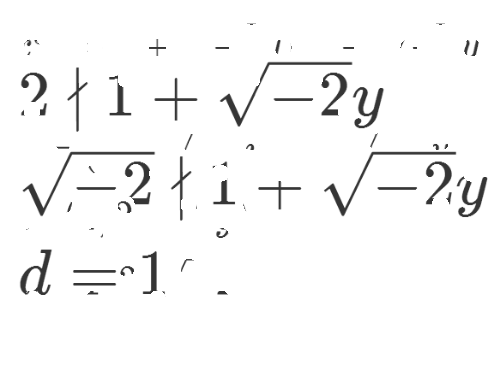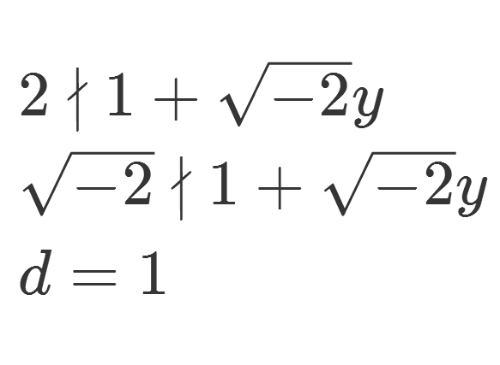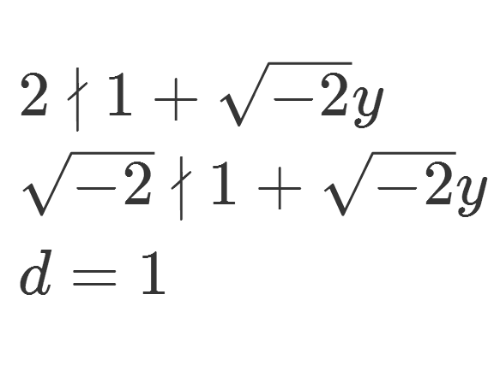
5、d等于1,说明右边两个因式是互素的,因此每个因式都只能是Q[sqrt(-2)]里面的代数整数的三次方,再分别考察实部和虚部。
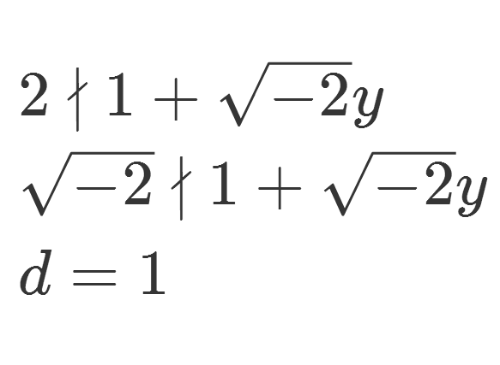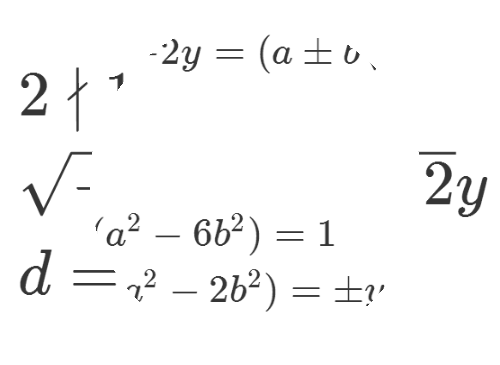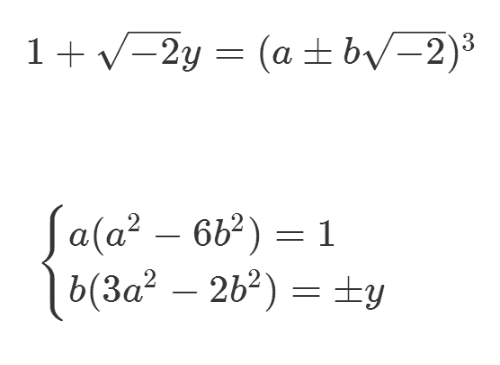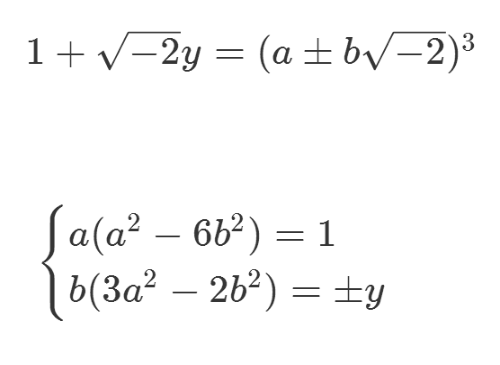
6、根据第一个式子,可以得到明确的结论:
a=1,b=0,y=0,x=1
于是,得到了这个不定方程的唯一的解。
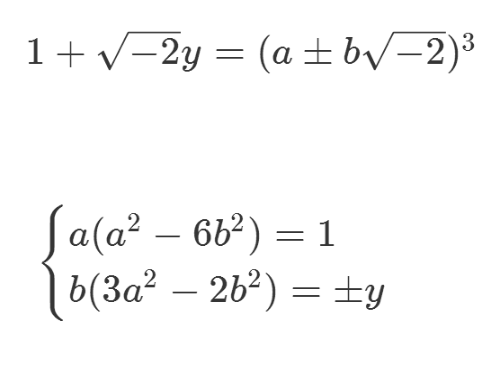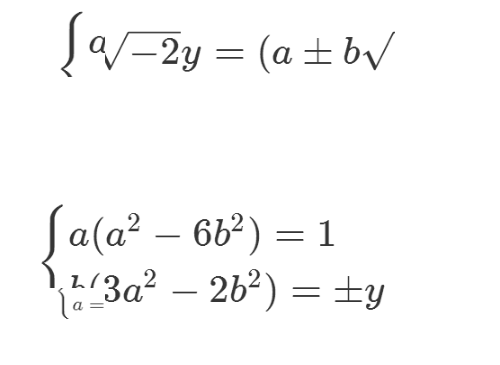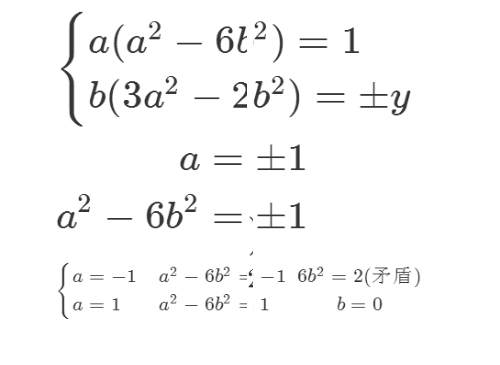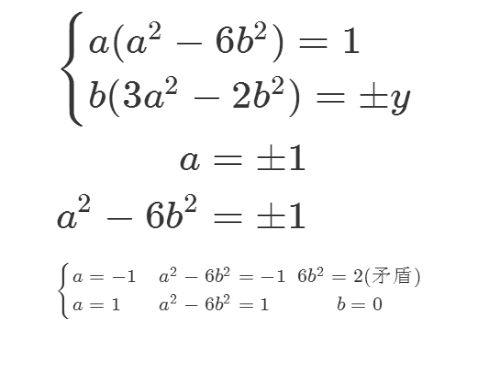
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:94
阅读量:151
阅读量:128
阅读量:154
阅读量:55