仿射变换下，椭圆有哪些不变的性质？

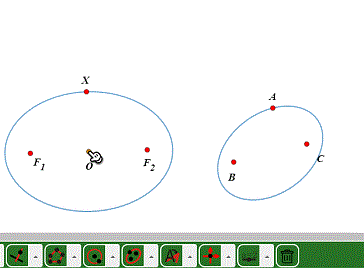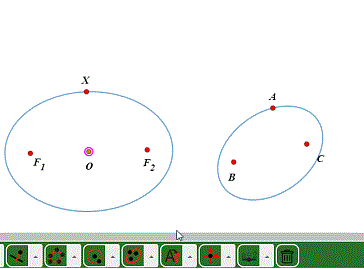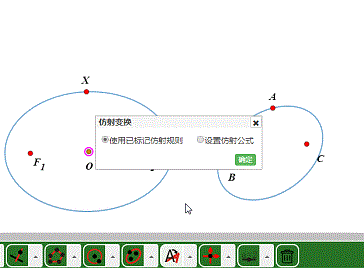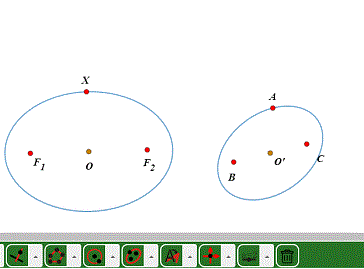
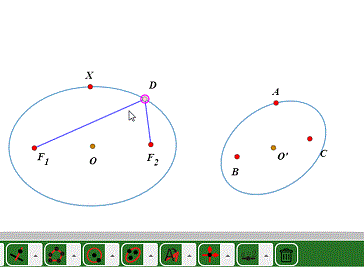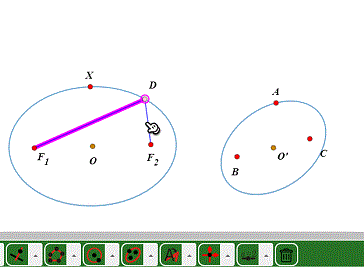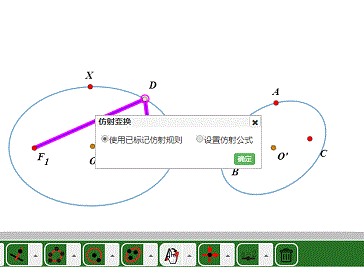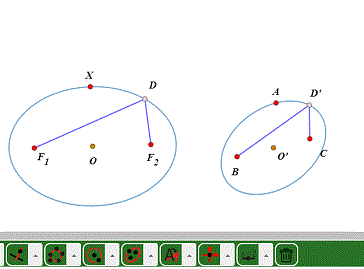
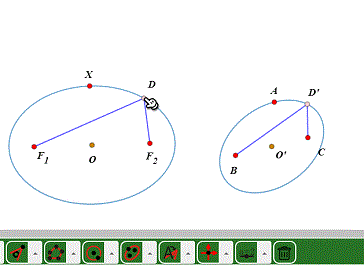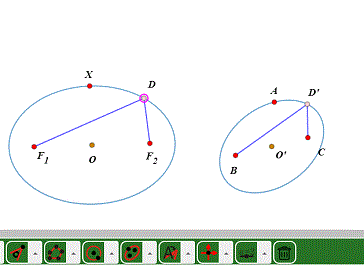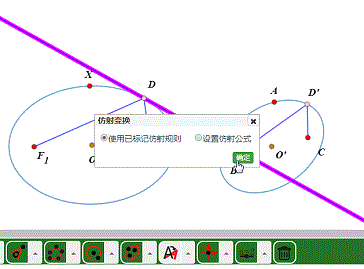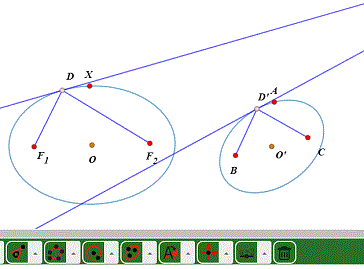
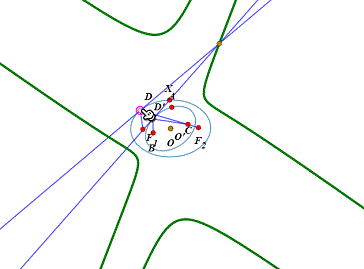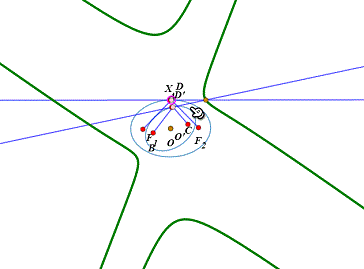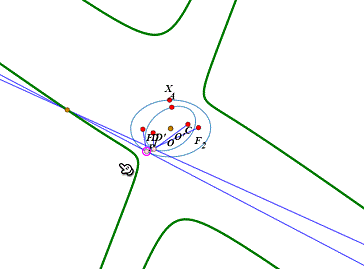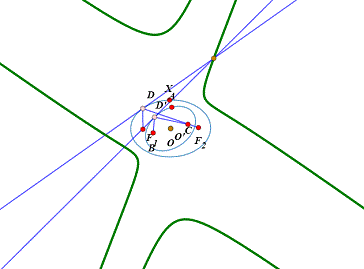
1、以F1、F2为焦点、X为椭圆上一点作椭圆。

2、标注X、F1、F2到A、B、C的仿射变换。

3、把椭圆变成另一个椭圆。

可以发现，椭圆的焦点经过仿射变换之后，已经不是另一个椭圆的焦点了。所以，椭圆的长轴和短轴的方向也改变了。

4、不过，椭圆的中心仍旧是椭圆的中心。

5、把D、线段DF1、DF2进行仿射变换。定长也变了，因为B、C根本就不是右边椭圆的焦点。

6、椭圆的切线仍旧是椭圆的切线。拖动D，可以看到两条线都与所在椭圆相切。

7、让两个椭圆的中心重合，过D和D'的切线的焦点的轨迹，是一条较复杂的曲线。