探究定积分求椭圆面积-的新思想---图形转化思想

1、关于椭圆和圆，我们观察他们的图形发现他们不是一个自变量对应一个函数值，所以想要利用定积分求面积就必须学会转化成几个部分求面积，比如中心在原点的椭圆，它在坐标轴四个象限的面积是相同的，我们就可以转化成求其中一个象限的面积。

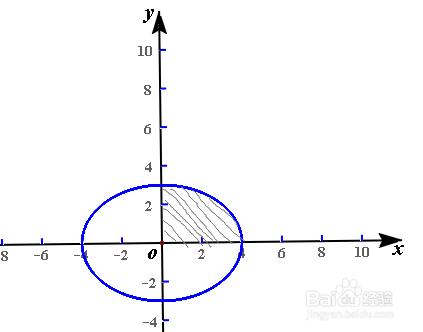
2、现在我们以：椭圆方程为x^2/16+y^2/9=1，求椭圆面积为例。来说明一下椭圆方程的转化问题。

3、接下来我们研究椭圆面积S椭圆，很显然椭圆面积是对第一象限积分值的四倍。我们来化简一下看有没有什么发现。

4、关于这个积分，以我们目前学的知识无法看出它的原函数，所以求解又出现了阻碍，那么有没有方法转化成我们学过的知识来求解呢？我们观察这个式子积分的部分很熟悉，好像和圆有某种联系。

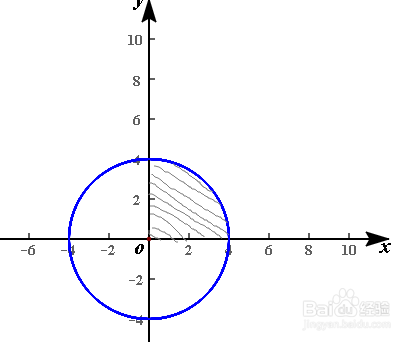
5、圆心在原点，半悄钸碌灵径为4的圆的面积为16π。它的四分之一为4π。根据四分之一圆的面积可以求得椭圆的面积3×4π=12π。观察椭圆方程发现长半轴锾攒揉敫a=4,b=3,这和面积中的3和4，是巧合吗?还是有一些联系？

6、看积分部分，可以表示为以原点为圆心，以a为半径的圆的四分之一。接下来我们推推看一般椭圆的面积公式。

7、这里我们利用图形转化思想，将积分转化成了圆面积的相关知识，不仅求得了椭圆的面积，还推理出了椭圆面积的一般表达式。这对我们以后的解题有很大的帮助。掌握这种思想会大大减少我们的计算，有事半功倍的作用。