浅谈无穷大与无界
1、我们从无穷大数列说起,首先明确这是一个用数列极限定义的概念,如果数列an满足liman=∞,则称an为无穷大数列,例如自然数列an=n。注意liman=∞只是一种方便的写法,意思是数列an发散(到∞),用数列极限的ε-N定义(这是数列极限的精确语言)表述为:对任意M>0,存在N,使得n>N时有|an|>M。再来看无界数列的定义,我们熟悉的是有界这个概念,它粗略地指数列各项只能在某个范围内取值,例如an=1/n是有界,由于an∈(0,1]。仿照数列极限的定义,可将有界定义为:存在M>0,使得对任意n,|an|≤M成立。我们把不是有界的数列定义为无界数列,根据对偶原理(“任意”与“存在”互换),可以得到无界的精确定义:对任意M>0,存在n,使得|an|>M。

2、分析上段给出的无穷大和无界的定义,可以发现它们的共同点在于都要求数列的某些项大于任意给定的正数M,而区别在于,无穷大量要求从某一确定的项aN起(N由事先选取的M决定),其后面的所有项(无限多项)都满足|an|>M;而无界量只要求满足|an|>M的n存在即可,至于有多少这样的项,以及这些项如何分布,都不做要求。由此可以看出,无穷大是比无界“更强”的概念,也就是说,无穷大量一定是无界量,但无界量不一定是无穷大量。
3、例如数列0,2,0,4,0,6,0,8,,, 显然此数列是无界的,因为其足够靠后的偶数项可以大过任意事先给定的正数M。但这个数列不是无穷大量,因为无穷大数列的定义要求,从数列的某项起,后面的所有项都要大于任意事先给定的M。可以看出这个数列不满足上述条件,因为不论从该数列的哪项起,后面都存在无穷多个0,这些0是不可能“大于任何事先给定的正数M”的。

4、类似地,函数中也可以定义无穷大和无界的概念,而且它们之间的关系完全和数列情况类似。例如考察函数f(x)=xsinx,它在R上是无界量,因为只需取x=2kπ+(π/2)即可(此时sinx=1,f(x)=2kπ+(π/2)随k的增大会大过任意事先给定的M);但它又不是无穷大量(当x趋于∞时),因为取x=kπ时,f(x)=0,即随着k的增大,函数值会无数次变为0,因此不管怎么选取X,都存在x>|X|使得f(x)=0,从而不满足|f(x)|>M的条件。
5、下图为函数f(x)=xsinx的图像,从图像角度结合定义,可以更加直观地理解无穷大和无界。粗略地说,无穷大量在x增大的过程中,|f(x)|虽然在局部上可以有小波动,但整体趋势上是稳定的(逐渐趋于∞),而无界量在x增大过程中|f(x)|在整体上可以有很大波动。事实上,后文的一个定理表明,非无穷大的无界量一定伴随着巨大波动。
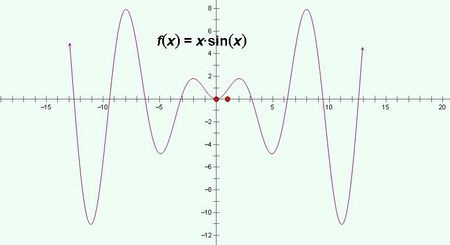
6、我们再从另一角度出发,借助数列极限的概念来描述函数的无穷大和无界。再次考察f(x)=xsinx,我们发现,在讨论中取x=2kπ+(π/2)和x’=kπ其实就是引入了两个数列。结合本例和数列极限的知识,可得用数列描述无穷大和无界的方法(证明略):若x趋于x0(或趋于∞)时,f(x)为无穷大量,则任意以x0为极限的数列xn,在f映射下得到的数列f(xn)都必定发散到∞。相应的,函数f(x)无界只需存在某一发散到∞的数列f(xn)即可。从这个角度看,函数f(x)=xsinx由于存在发散数列f(xn)=[2nπ+(π/2) ]sin[2nπ+(π/2)]从而是无界量,又由于存在收敛数列f(xn)'=(nπ)sin(nπ)从而不是无穷大量。更深入的理论表明,对于一个非无穷大的无界量,必定存在这样两个数列f(xn),其中一个发散至∞,另一个收敛。

7、对于数列的无穷大与无界,也可用类似方法描述,为此需要利用子列的概念。从一个数列an中取出一部分项构成一个新数列,称为数列an的一个子列,记作ank,项ank表示它是子列中的第k项,在原数列中是第nk项。例如an=n,则偶数列2,4,6...是an的一个子列,an1为子列中的第一项2,它在原数列中是第二项,因此n1=2。用子列来描述数列的无穷大和无界如下:无穷大数列的任意子列都发散至无穷大,无界数列只需存在一个发散至无穷大的子列即可。

8、最后以一个“期末考试”难度的习题结束本文,如果你理解了本文所讲内容,解决本题应该是“手到擒来”的。
