【平面几何】一个30°角和40°角的角格点问题

1、我初步看到这个问题，首先想到的是，线段BC绕着某个点旋转到AD的位置上，因此，我需要来确定这个旋转轴心。

方法很简单，线段AC和线段BD的垂直平分线的交点U，即为旋转轴心。

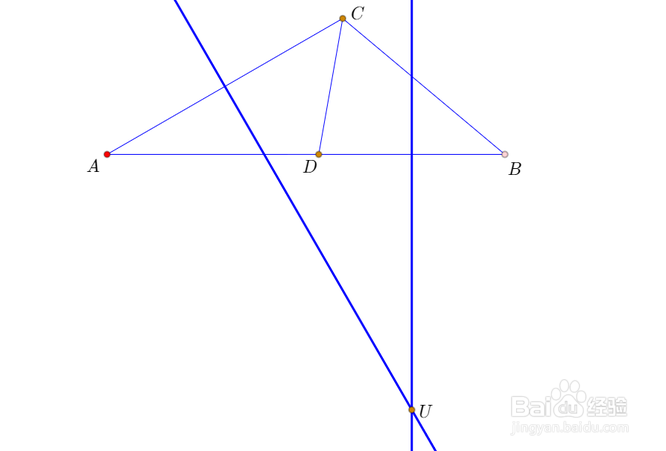
2、这样的话，△UAD全等于△UCB。

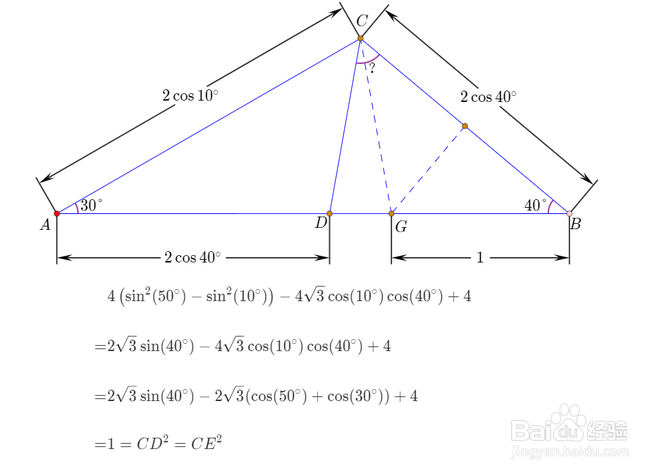
3、设UC和AB交于G，初步猜测CD=CG。

4、注意到，CG=BG，因此，可以假设BG=1，这样，AC、BC、AD的长度就可以计算出来。

5、再在△CAD里面，应用余弦定理，可以算出CD的长度来。

具体过程，如下图所示。

证得CD=CG之后，∠BCD=60°就是显而易见的结论了。

6、然而，上述方法很不完美，而且，计算过程也比较复杂。

为此，我需要寻求纯几何方法。

经过一番思考，得之。

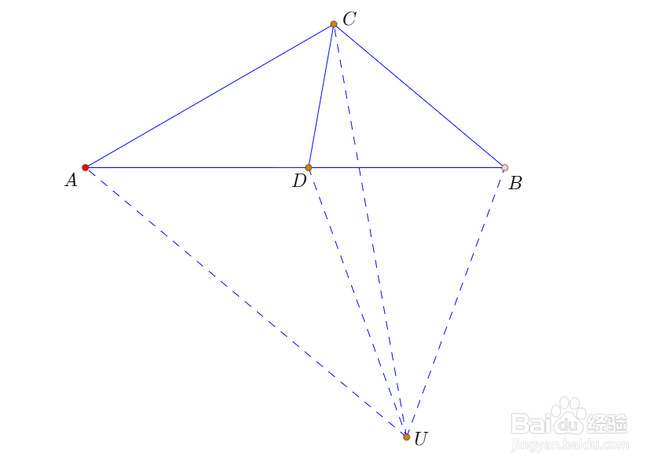
1、注意到BC到AD，是旋转了40°角，所以∠BUD=∠CUA=40°；

因为AU=CU，所以∠UAC=70°，∠UAB=40°，AU//BC；

因为BU=DU，所以∠ABU=70°，所以AB=AU=BC；

这说明AUBC是等腰梯形，CA=BU，进而确定∠CUD=10°。

2、取AC中点E，那么UE是线段AC的垂直平分线，又是∠CUA的平分线；

所以∠CUE=20°，UD平分∠CUE。

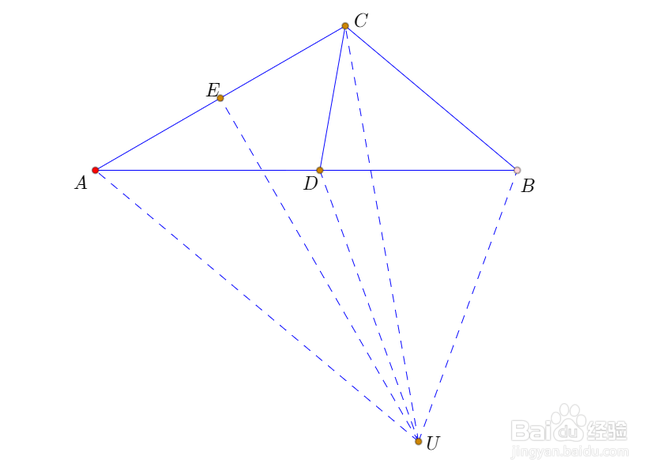
3、设CE交AB于F；

因为∠AUE=20°，所以∠UFD=60°。

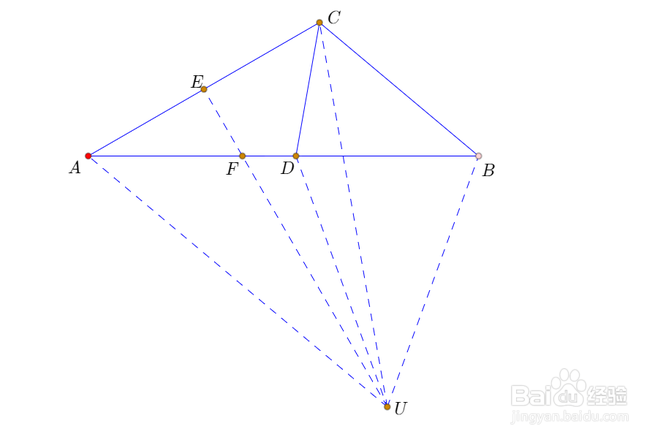
4、连接CF，可知CF=AF，所以∠CFD=60°。

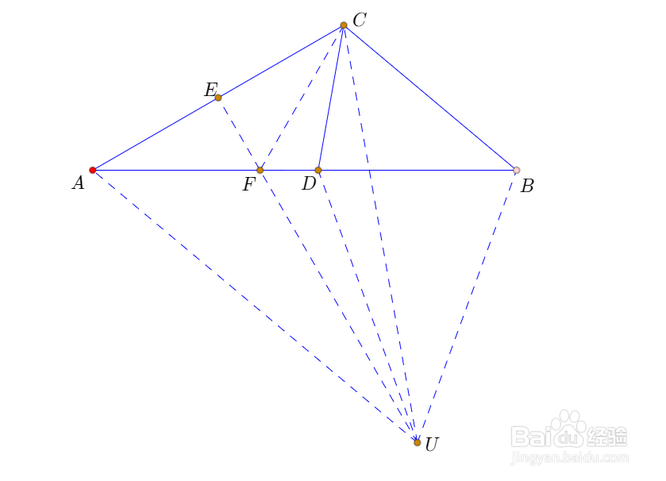
5、综上所述，D必为△UCF的内心，CD平分∠UCF；

注意到∠UCF=∠UAF=40°，所以∠UCD=20°，所以∠BCD=60°。

问题就这么轻松的解开了。

然而，这个思考过程却不那么容易，全是智慧的结晶啊。