Matlab实现“与”逻辑运算的单层神经网络感知器

1、双击matlab桌面图标，进入matlab工作区域 

2、首先我们展示了“与”逻辑运算的基本规则：

0 and 0=0

0 and 1=1

1 and 0=0

1 and 1=1

也就是说，我们需要在输入（0， 0），（0，1），（1，0），（1，1）时输出（0，0，0，1）

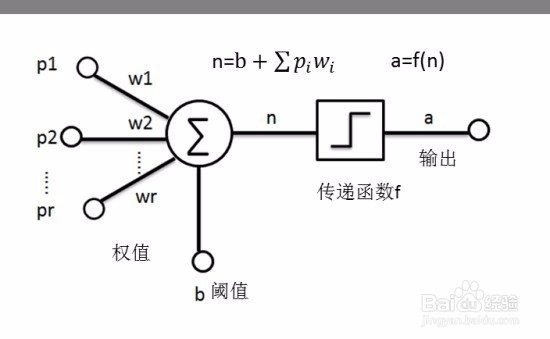
3、为解决这样一个“与”逻辑运算问题，我们构建了一个简单的单层神经网络感知器模型，如下图所示。输入为p1，p2，...，pn。权值为w1,w2,w3,...wn。神经元阈值为b。传递函数为f。输出为a

在该问题中，只有两个输入，故

a=f(p1w1+p2w2+b)

4、在上述的单层神经网络感知器模型中，我们选择一个阶跃函数作为传递函数。当自变量的值大于0，函数值为1,；自变量的值小于0，函数值为0.

在matlab中使用hardlim 作为阶跃函数。

5、感知器的学习规则也是一种训练方法，目的是不断调整权值和阈值。

6、代码实现如下图所示，将第一步的四个样本进行5次迭代训练，即可构建解决问题感知器。

往模型中输入（0， 0），（0，1），（1，0），（1，1），输出（0，0，0，1）。

MATLAB代码如下：

close all;

clear;

w=[1 1];b=0;%随机设置初始权值与阈值

%p,t为给定的训练样本，p为输入，t为对应的输出

%And计算网络迭代训练五次

p=[0 0;0 1;1 0;1 1];

t=[0;0;0;1];

p1=[p;p;p;p;p]

t1=[t;t;t;t;t]

%训练过程传递函数为阶跃函数

for i=1:20

    a=hardlim(p1(i,1:2)*w'+b);

    e=t1(i,1)-a;

    w=w+e*p1(i,1:2);b=b+e;

end

%网络输出

 a=hardlim(p(1:4,1:2)*w'+b)