一般式方程的法向量和方向向量

法向量一般直接看系数，,面的标准方程是ax+by+cz+d=0.法向量就是是（a,b,c）；

方向向量一芫王墙错般指的是线的方向向量.线可以由参数方程构成,也可以由2个面来表示.线的标准参数方程x=lt+a,y=mt+b,z=nt+c.方向向量是（l,m,n）。

一、法向量的求解

1、首先对该立体图形建立坐标系，如果能建，则可求面的法向量 ：

2、尽量在图中找到垂直于面的向量 ；

3、如果找不到，那么就设法向量n=（x,y,z）， 然后因为法向量垂直于面，所以n垂直于面内两相交直线，可列出两个含有x、y、z的方程，两个方程中有三个未知数，解不出一个唯一的解。

但可以根据题目情况、计算方便，使z（或x或y）等于一个具体的数，就变成了两个未知量两个方程的方程组了，是可解方程组，解出唯一的解，就是设的那个法向量n(x,y,z)了。

扩展资料：

方向向量的求解

只要给定直线，便可构造两个方向向量（以原点为起点）。

（1）即已知直线l：ax+by+c=0，则直线l的方向向量为

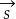
=(-b,a)或(b,-a)；

（2）若直线l的斜率为k,则l的一个方向向量为

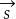
=(1,k)；

（3）若A(x1,y1),B(x2,y2),则AB所在直线的一个方向向量为

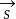
=(x2-x1,y2-y1)。