寻找《水仙花数》的Mathematica算法剖析
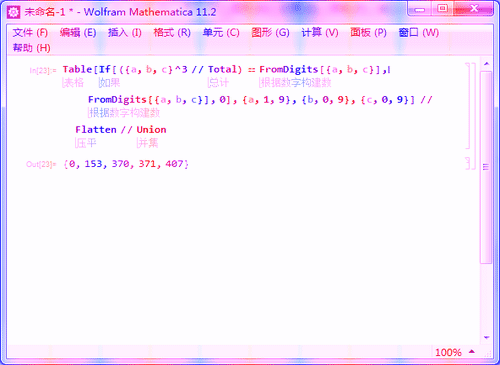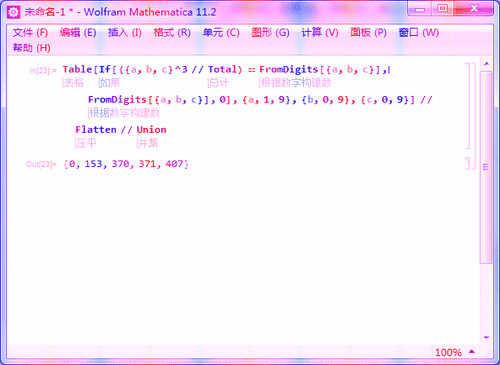
1、Table[If[({a, b, c}^3 // Total) == FromDigits[{a, b, c}],
FromDigits[{a, b, c}], 0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9}] //
Flatten // Union
得到四个三位数的水仙花数。
2、FromDigits[{a, b, c}]的作用是把三个数字串成一个数。

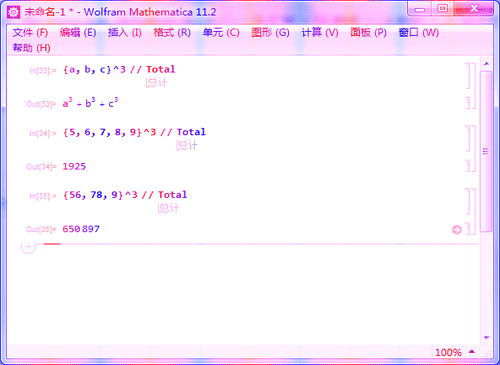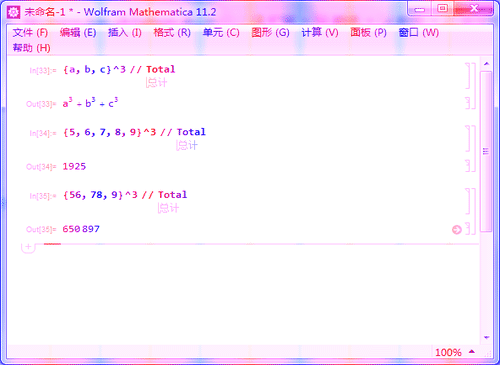
3、{a, b, c}^3 // Total
计算a、b、c的立方和。
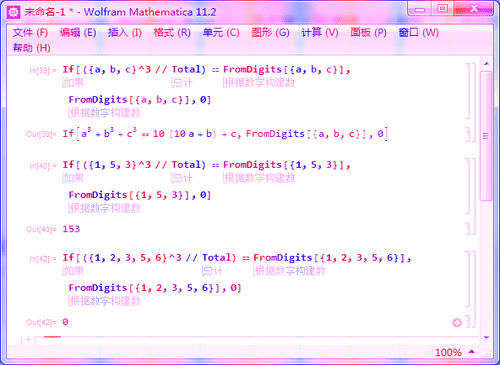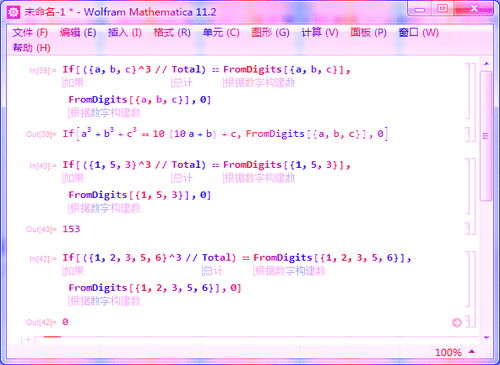
4、用If语句作出判断:
If[({a, b, c}^3 // Total) == FromDigits[{a, b, c}], FromDigits[{a, b, c}], 0]
如果a, b, c的立方和等于a, b, c串成的数字,那么这个数字就是三位数的水仙花数,保留下来;
否则,用0代替。
5、让a, b, c分别遍历0到9:
Table[If[({a, b, c}^3 // Total) == FromDigits[{a, b, c}],
FromDigits[{a, b, c}], 0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9}]
注意,a等于0没意义,不是三位数了。

6、把结果提取出来:
Table[If[({a, b, c}^3 // Total) == FromDigits[{a, b, c}],
FromDigits[{a, b, c}], 0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9}] //
Flatten // Union
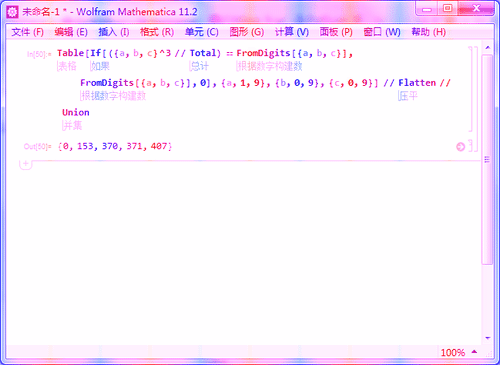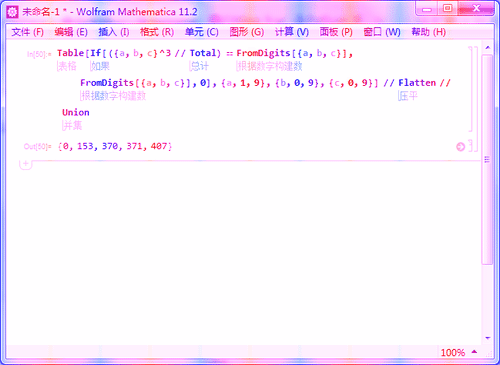
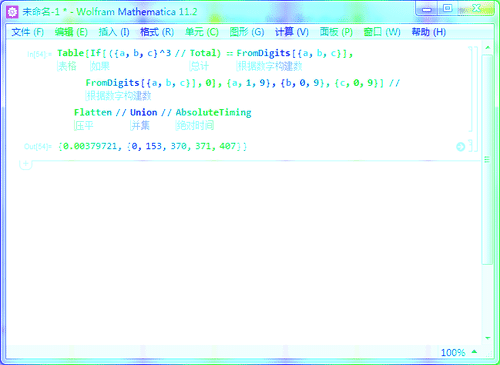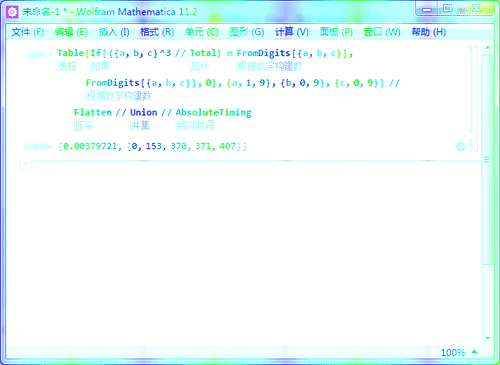
7、查看计算时间:
Table[If[({a, b, c}^3 // Total) == FromDigits[{a, b, c}],
FromDigits[{a, b, c}], 0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9}] //
Flatten // Union // AbsoluteTiming
用时不超过0.004秒。
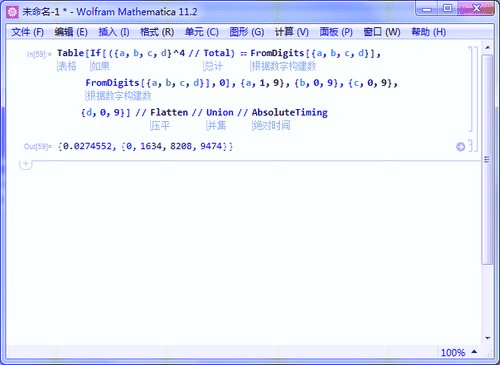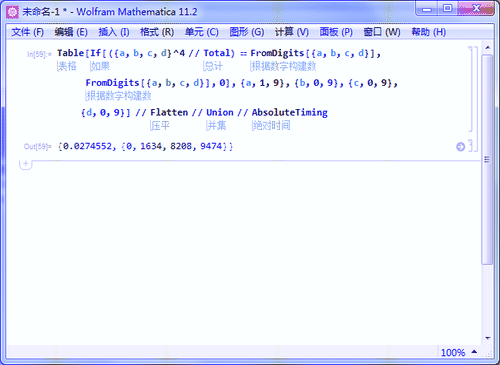
8、用时0.03秒,可以找到全部三个四位数水仙花数:
Table[If[({a, b, c, d}^4 // Total) == FromDigits[{a, b, c, d}],
FromDigits[{a, b, c, d}], 0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9}, {d, 0, 9}]
// Flatten // Union // AbsoluteTiming
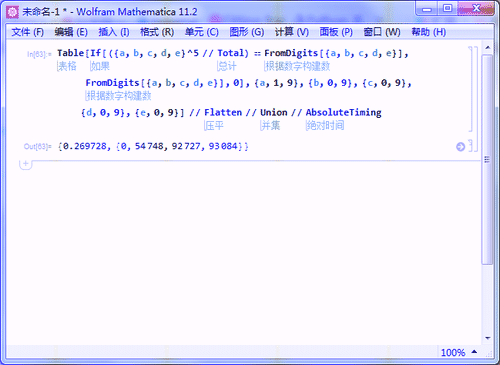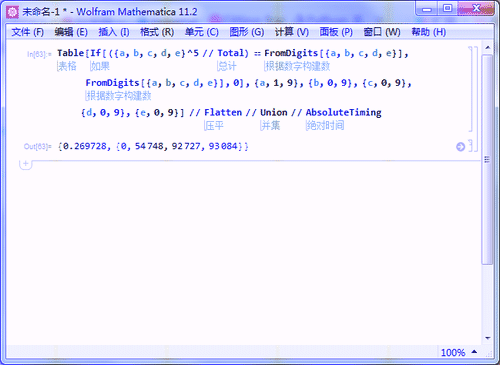
9、用时0.269秒左右,找到全部三个五位数水仙花数:
Table[If[({a, b, c, d, e}^5 // Total) == FromDigits[{a, b, c, d, e}],
FromDigits[{a, b, c, d, e}], 0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9},
{d, 0, 9}, {e, 0, 9}] // Flatten // Union // AbsoluteTiming
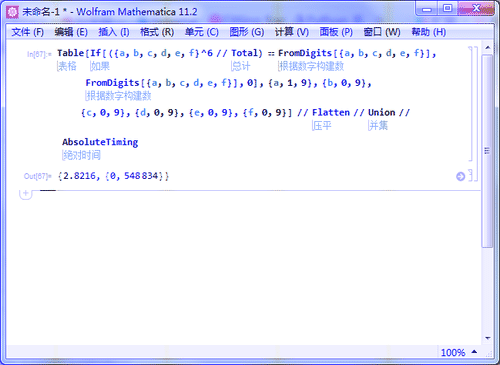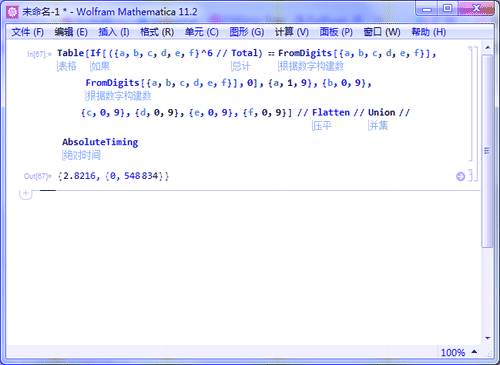
10、6位数的水仙花数只找到一个:
Table[If[({a, b, c, d, e, f}^6 // Total) ==
FromDigits[{a, b, c, d, e, f}], FromDigits[{a, b, c, d, e, f}],
0], {a, 1, 9}, {b, 0, 9}, {c, 0, 9}, {d, 0, 9}, {e, 0, 9}, {f, 0,
9}] // Flatten // Union // AbsoluteTiming
耗时将近3秒左右。