求解分式函数y=(3x+1)^2/(2x^3+2x-5)的多阶导数

1、用对数函数和函数商的求导法则等知识，介绍分式函数y=(3x+1)^2/(2x^3+2x-5)的导数的主要方法和步骤。

2、对数法求解函数y的一阶导数，主要用到对数函数的求导公式，具体步骤如下。

∵y=(3x+1)^2/(2x^3+2x-5)，

∴lny=ln(3x+1)^2/(2x^3+2x-5),即：

lny=ln(3x+1)2-ln(2x3+2x-5)，

lny=2ln(3x+1)-ln(2x3+2x-5)，两边求导。

3、过程进行化简，变形即可得到一阶导数y'的最终结果。

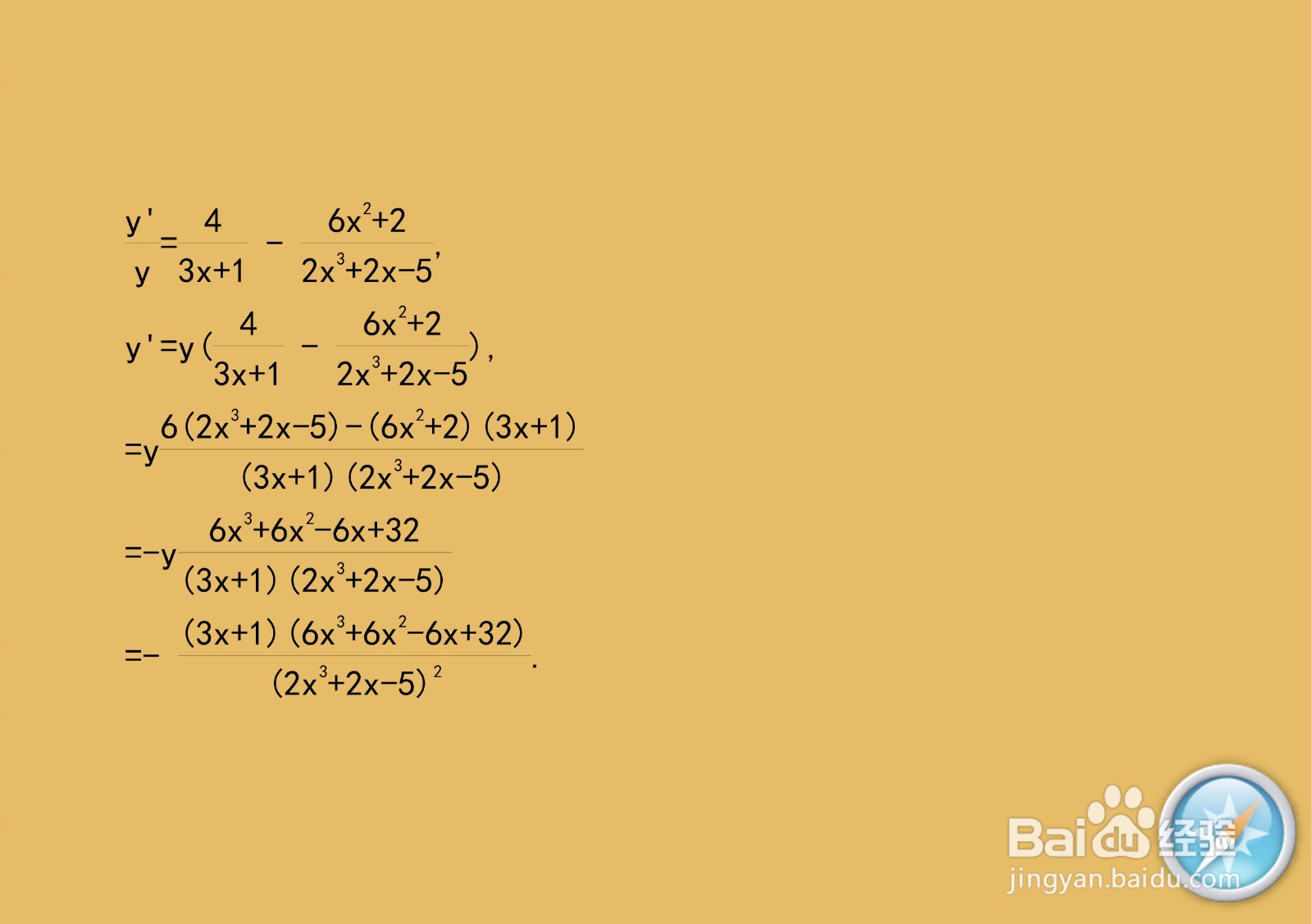
4、使用函数商的求导法则，也即可计算出函数的一阶导数。

5、利用函数乘积求导法则，计算求解函数y的二阶导数。

y'(2x3+2x-5)2=(3x+1)(6x3+6x2-6x+32)，

设w=6x3+6x2-6x+32，

则w'=18x2+12x-6，代入得：

两边再次对x求导得：

y"(2x3+2x-5)2+2y'(2x3+2x-5)(6x2+2x) 

=3w+(3x+1)w',则：

y"(2x3+2x-5)2=3w+(3x+1)w'-2y'(2x3+2x-5)(6x2+2x)，

y"(2x3+2x-5)2=3w+(3x+1)w'+2(6x2+2x)，

6、变形化简二阶导数过程,即可计算出函数的二阶导数y''.

7、再次使用函数商的求导法则，计算该函数的二阶导数y''步骤如下：

u=(3x+1)(6x3+6x2-6x+32)，w=6x3+6x2-6x+32，v=(2x3+2x-5)2，

u'=3w+(2x+1)w'，v'=2(6x2+2x)(2x3+2x-5)，

w'=18x2+12x-6，代入得：