含2kπ+α诱导类型三角函数的不定积分

本经验介绍含2kπ+α诱导类型三角函数的不定积分，即求∫si艘绒庳焰n(2kπ+α)dα，∫cos(2kπ+α)dα，∫tan(2kπ+α)dα，∫cot(2kπ+α)dα，∫sec(2kπ+α)dα，∫csc(2kπ+α)dα的步骤。

工具/原料

三角函数基本知识

不定积分基本知识

1.含2kπ+α的诱导公式

1、sin(2kπ+α)=sin αcos(2kπ+α)=cos αtan(2kπ+α)=tan αcot(2kπ+α)=cot αsec(2kπ+α)=sec αcsc(2kπ+α)=csc α

2.sin(2kπ+α)的不定积分

1、∫sin(2kπ+α)dα=∫sin(2kπ+α)d(2kπ+α)=-cos(2kπ+α)+c=-cosα+c

2、图例解析如下：

3.cos(2kπ+α)的不定积分

1、∫cos(2kπ+α)dα=∫cos(2kπ+α)d(2kπ+α)=sina(2kπ+α)+c=sinα+c

2、图例解析如下：

4.tan(2kπ+α)的不定积分

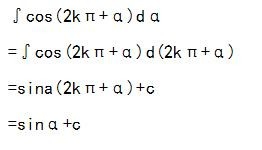
1、∫tan(2kπ+α)d拿骛蟊痊α=∫[sin(2kπ+α) d(2kπ+α)/ cos(2kπ+α)]=-∫d cos(2kπ+α)/cos(2kπ+α)=-ln|cos(2kπ+α)|+c=-ln|cosα|+c

2、图例解析如下：

5.cot(2kπ+α)的不定积分

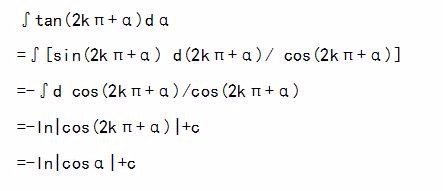
1、∫ctg(2kπ+α)dα=∫[cos(2kπ+α) d(2kπ+α)/ sin(2kπ+α)]=∫d sin(2kπ+α)/sin(2kπ+α)=ln|sin(2kπ+α)|+c=ln|sinα|+c

2、图例解析如下：

6.sec(2kπ+α)的不定积分

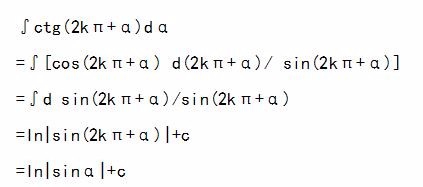
1、∫sec(2kπ+α)d拿骛蟊痊α=∫dα/ cos(2kπ+α)=∫d(2kπ+α)/ cos(2kπ+α)=∫cos(2kπ+α)d(2娱浣嫁装kπ+α)/ [cos(2kπ+α)]^2=∫dsin(2kπ+α)/ {1-[sin(2kπ+α)]^2}=∫dsin(2kπ+α)/ {[1-sin(2kπ+α)][1+ sin(2kπ+α)]}=(1/2){∫dsin(2kπ+α)/ [1-sin(2kπ+α)]+∫dsin(2kπ+α)/ [1+sin(2kπ+α)]}=(1/2)ln{[1+sin(2kπ+α)]/ [1-sin(2kπ+α)]}+c=(1/2)ln[(1+sinα)/(1-sinα)]+c=(1/2)ln[(1+sinα)^2/(cosα)^2]+c=ln|(1+sinα)/cosα|+c=ln|secα+tana|+c

2、图例解析如下：

7.csc(2kπ+α)的不定积分

1、∫csc(2kπ+α)d拿骛蟊痊α=∫dα/ sin(2kπ+α)=∫d(2kπ+α)/ sin(2kπ+α)=∫sin(2kπ+α)d(2娱浣嫁装kπ+α)/ [sin(2kπ+α)]^2=-∫dcos(2kπ+α)/ {1-[cos(2kπ+α)]^2}=-∫dcos(2kπ+α)/ {[1-cos(2kπ+α)][1+ cos(2kπ+α)]}=-(1/2){∫dcos(2kπ+α)/ [1-cos(2kπ+α)]+∫dcos(2kπ+α)/ [1+cos(2kπ+α)]}=-(1/2)ln{[1+cos(2kπ+α)]/ [1-cos(2kπ+α)]}+c=-(1/2)ln[(1+cosα)/(1-cosα)]+c=-(1/2)ln[(1+cosα)^2/(sinα)^2]+c=-ln|(1+cosα)/sinα|+c=-ln|cscα+ctga|+c

2、图例解析如下：