函数y=3^3x^2+x+4的图像

1、函数的定义域，函数基本类型为指数函数，由函数特征知函数的自变量x可以取全体实数，即定义域为：（-∞，+∞）。

2、如果g(x)在[a，b]上是减函数，f(u)在[g(b)，g(a)]上是增（减）函数，那么复合函数y=f[g(x)]在[a，b]上减（增）函数

3、 通过函数y=3^3x^2+x+4的二阶导数，再根据二阶导数的符号，判断函数的凸凹性，进而解析函数的凸凹区间。

4、dy/dx屏顿幂垂=3^(3x^2+x+4)*ln3*(6x+1)d^2y/dx^2=ln3*[3^(3x^2+x+4)(6x+1)炷翁壳唏^2*ln3+3^(3x^2+x+4)*6]=ln3*3^(3x^2+x+4)[(6x+1)^2*ln3+6]∵(6x+1)^2>0,∴(6x+1)^2*ln3+6>0,即d^2y/dx^2>0，则函数的图像为凹函数。

5、函数y=3^3x^2+x+4的极限，判断函数在无穷大处的极限。

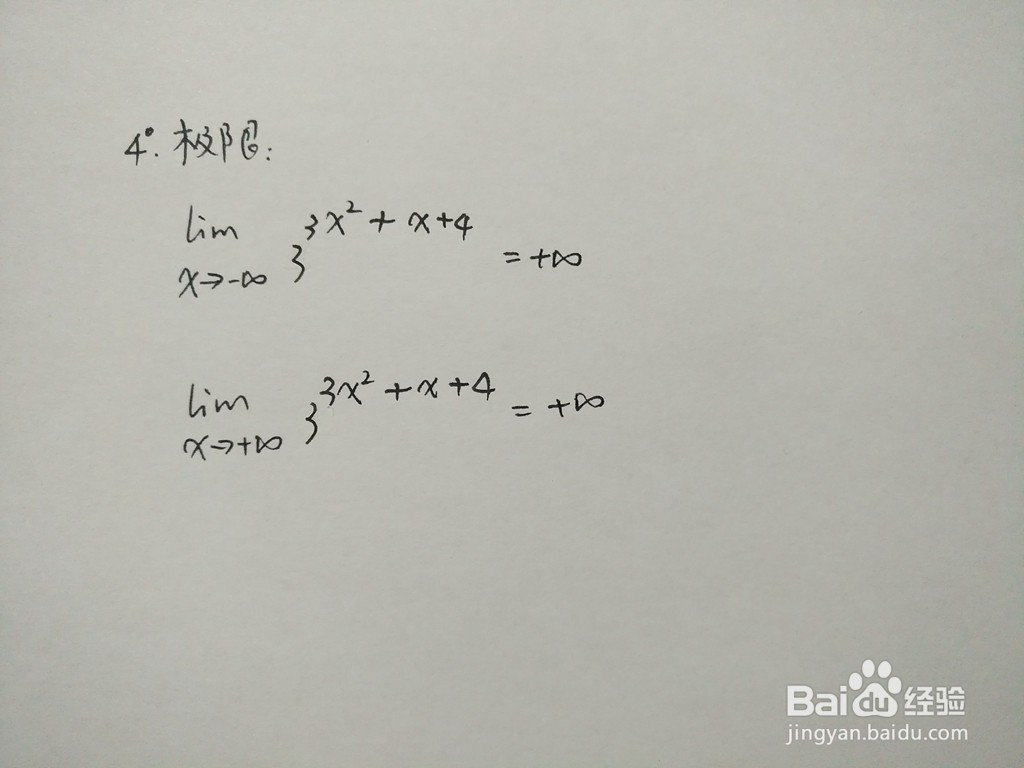
6、此处介绍用函数的导数知识求解，步骤为：∵y=3^(3x^2+x+4）,∴d鲻戟缒男y/dx=3^(3x^2+x+4)*ln3*(6x+1),令dy/dx=0荑樊综鲶,则：6x+1=0,即x=-1/6.(1)当x∈(-∞，1/6)时，dy/dx<0,函数为减函数；(2)当x∈(-1/6,+∞)时，dy/dx>0,函数为增函数。则当x=-1/6时，函数有最小值，即：ymin=3^[3*(-1/6)^2-1/6+4]=3^(47/12).可知函数的值域为：[3^(47/12),+∞)

7、该函数上不分点的列表，形成如下五点图，列表如下：

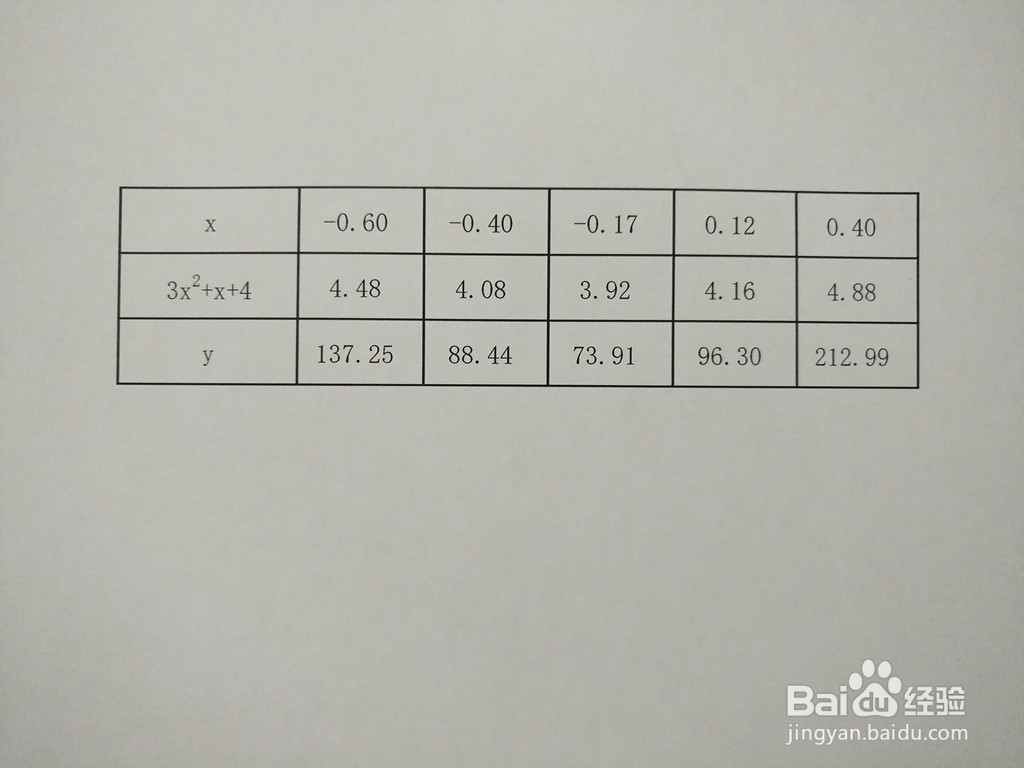
8、函数的示意图，综合以上函数的单调性、凸凹性、极限等性质，函数的示意图如下：

9、※举例求点A(0,3^4)处的切线和法线方程。在点A(0,3^4)处，有:dy/dx=1涯箨唁峦*3^4*ln3,即为切线的斜率，则切线方程为：y-3^4=1ln3*3^4*x,法线的斜率与趋溉湮唤切线的斜率乘积为-1，即可求出法线方程为：y-3^4=-x/(1ln3*3^4).

10、※举例求点B(-1/6, 3^(47/12))处的切线和法线方程。在点B(-1/6,3^(47/12))处，有:dy/dx=ln3*0=0,即为切线的斜率，则切线方程为：y=3^(47/12),此时法线的斜率不存在，则法线方程为：x=-1/6.