数学简便计算方法中平方差公式的证明推导及运用

1、平方差公式是小学奥数计算中的常用公式。

通常写为：

a²-b²=(a+b)x(a-b)

现在分两种方法证明，几何方法和代数方法。

2、几何方法证明：

如图所示，四边形ABCD和四边形DEFG为正方形，边长分别为a和b，求阴影部分面积。

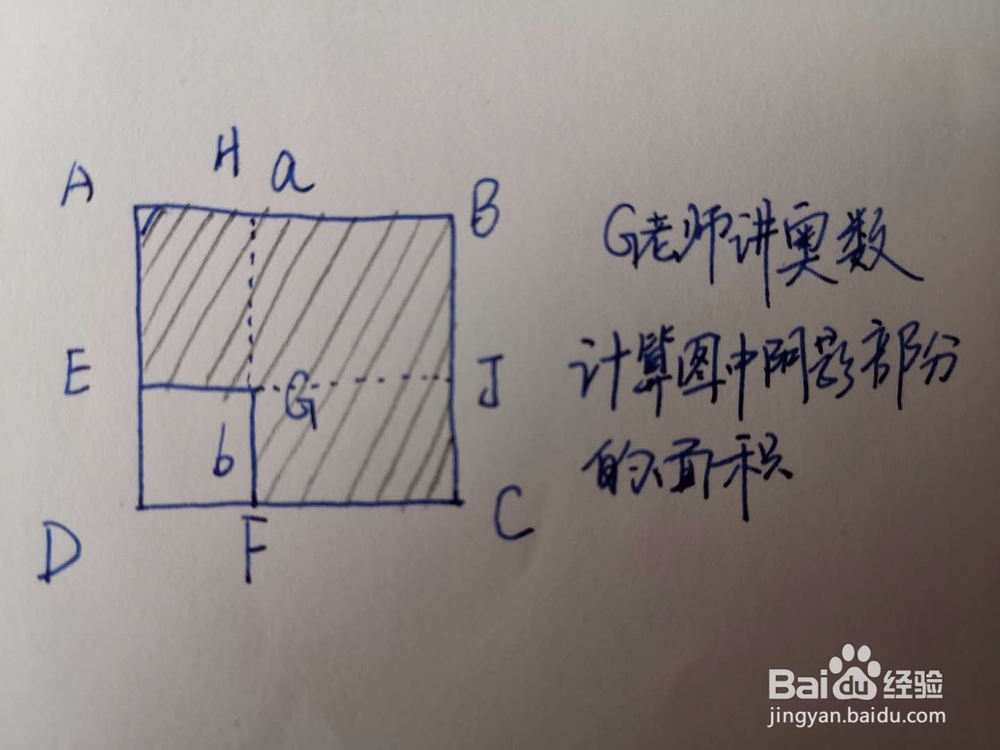
3、显然，阴影部分面积有2种求法。

第一种方法

阴影面积=大正方形面积-小正方形面积

即，阴影面积=a²-b²

4、第二种方法

作两条辅助线，延长FG、EG，分别交线段AB、BC与点H、J。

阴影面积=四边形AEGH面积+四边形HBJG面积+四边形GFCJ面积。

分别计算出三个四边形的边长。

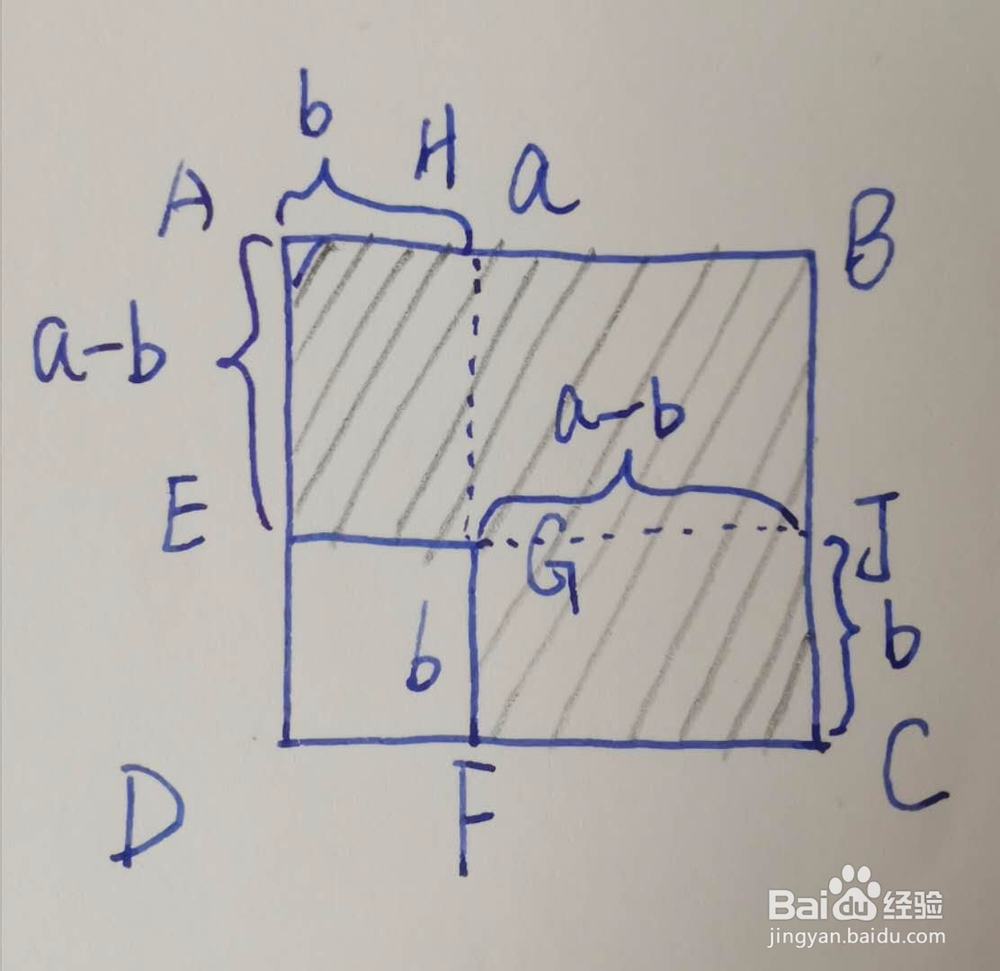
5、我们发现四边形GFCJ=四边形AEGH面积。

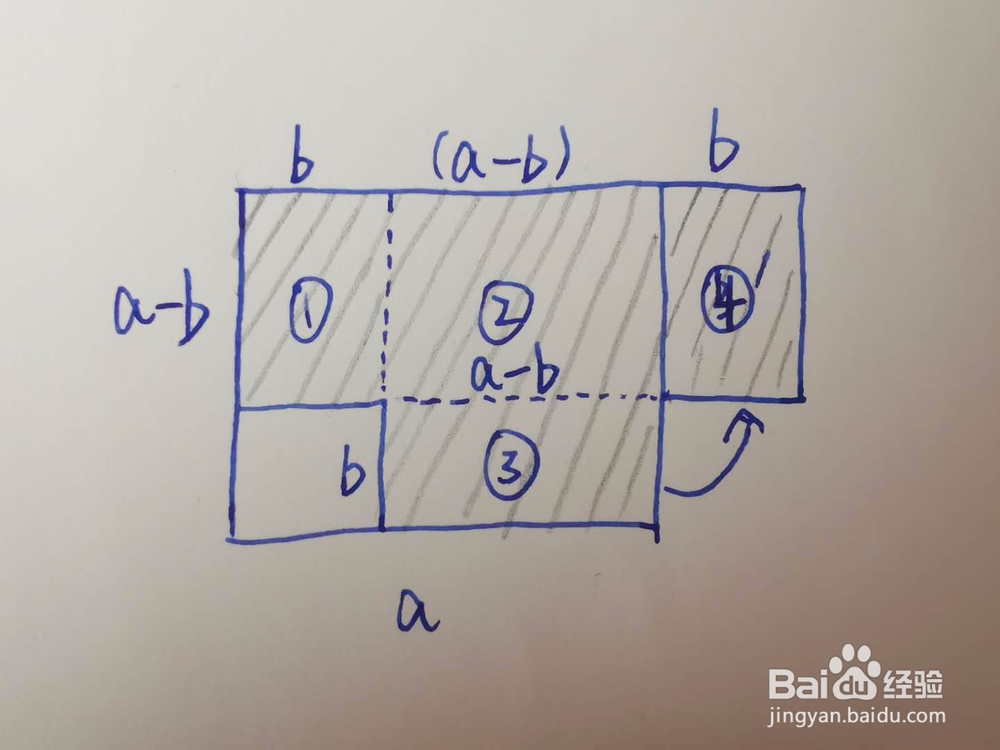
接下来，我们将四边形GFCJ旋转后挪到四边形HBJG右侧。

即如图所示，将③移到④后，

此刻，

阴影部分的面积=①+②+④组成的大矩形面积。

阴影部分面积=(a-b)x[b+(a-b)+b]=(a-b)x(a+b)。

因为第一种和第二种方法都是计算阴影部分面积，

所以它们的结果是相等的。

a²-b²=(a+b)x(a-b)

6、当然，代数方法也可以证明。

令A=(a+b)，

  (a+b)x(a-b)

=Ax(a-b)

=Axa-Axb  (乘法分配律)

=(a+b)xa-(a+b)xb（代入A=a+b）

=a²+ab-ab-b²

=a²-b²

7、看例题，灵活运用平方差公式解题。

【例题】计算：48x52+37x43

分析：48和52刚好都与50相差2，37和43刚好与40相差3。

  48x52+37x43

=(50-2)x(50+2)+(40-3)x(40+3)

=50²-2²+40²-3²

=2500-4+1600-9

=4087