曲面拟合的难处在哪里？

1、给出一幅单通道图片。

2、为了节省计算时间，这里把图片缩小。

img = ImageResize[img, 30]

3、获取图片数据：

data=ImageData[img]

4、把每一个像素的坐标转化为点坐标，并把像素值转化为数据集，得到一个三元数据集：

shuju = Flatten[

  Table[{m, n, data[[m, n]]}, {m, 1, Length[data], 1}, {n, 1, 

    Length[data[[1]]], 1}], 1]

5、画出数据的散点图：

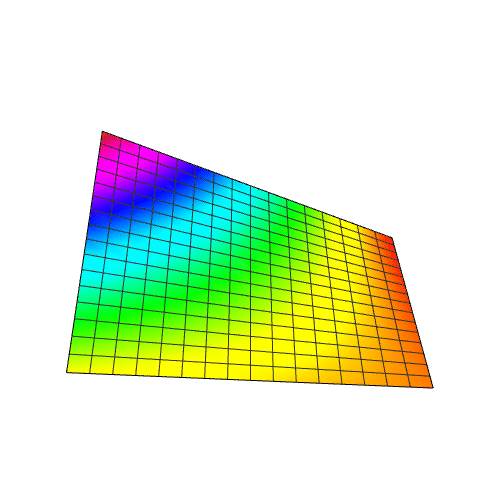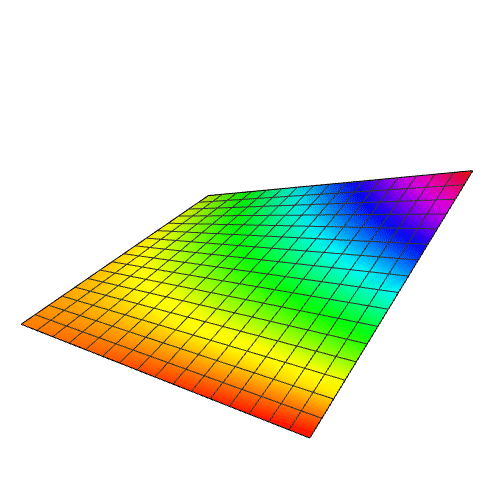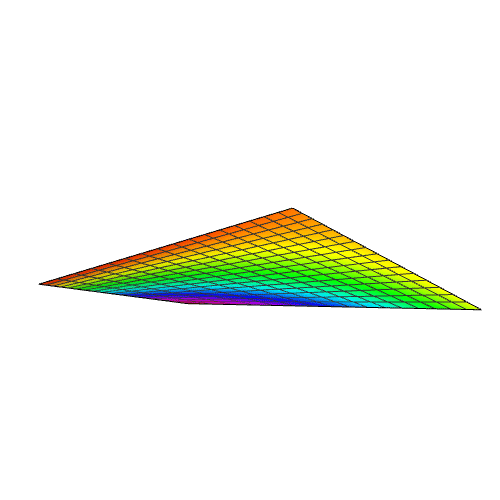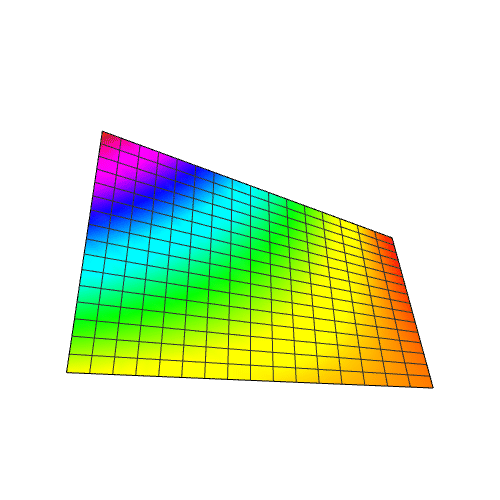
sandiantu = ListPlot3D[shuju, PlotRange -> All]

6、用一种方案拟合数据：

nihe = Fit[shuju, {1, x, y, x y}, {x, y}]

并画出曲面图：

Plot3D[nihe, {x, 1, 30}, {y, 1, 30}]

与上面的散点图相差甚远。

7、改变拟合方案，增加复杂度：

nihe = Fit[

  shuju, {x, y, x y, x^2, y^2, x^3, y^2, x y^2, x^2 y, x^4, y^4, 

   x y^3, x^3 y, x^2 y^2}, {x, y}]

看样子，复杂度还是不够。

8、引进正弦函数：

nihe = Fit[shuju, 

  Sin /@ {x, y, x y, x^2, y^2, x^3, y^2, x y^2, x^2 y}, {x, y}]

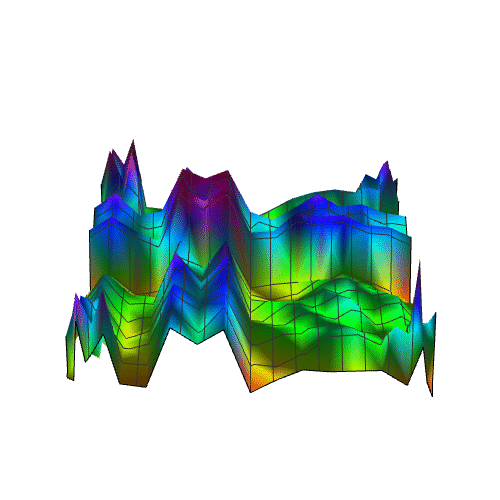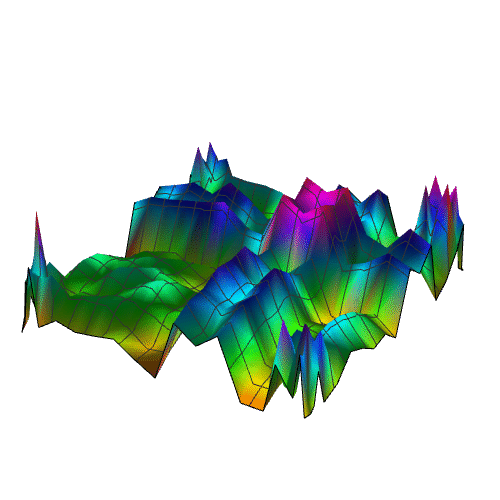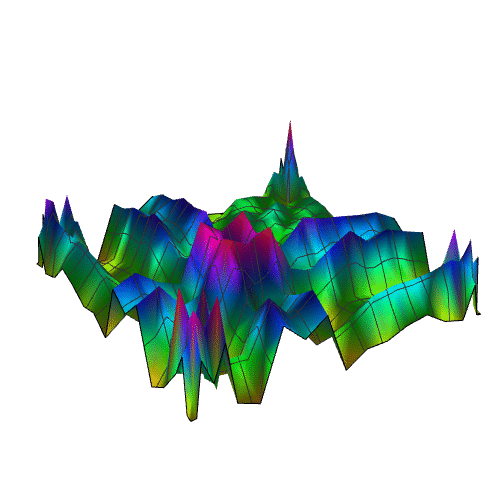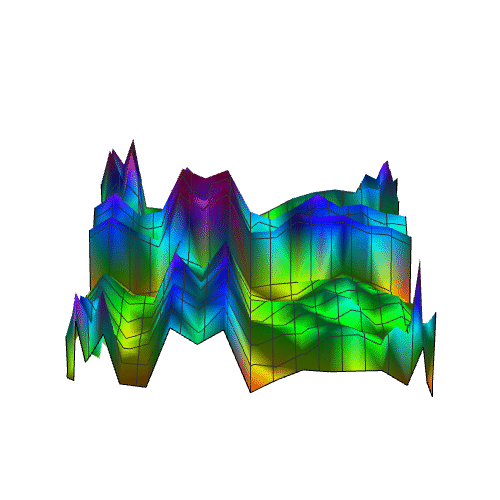
9、再增加复杂度：

nihe = Fit[shuju, 

  Flatten[{a0 = 

     Flatten[{1, Table[x^m y^n, {m, 1, 9, 1}, {n, 1, 9, 1}]}], 

    Sin /@ a0}], {x, y}]

10、出图效果。

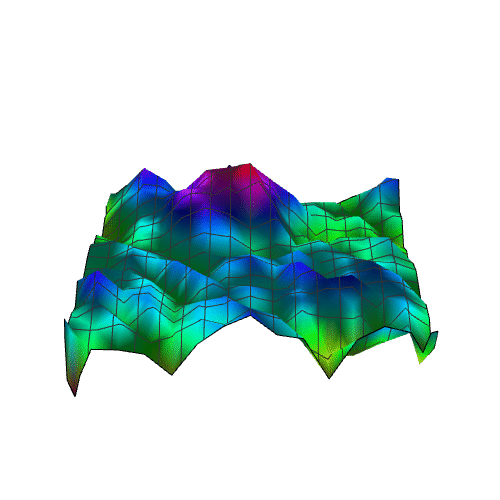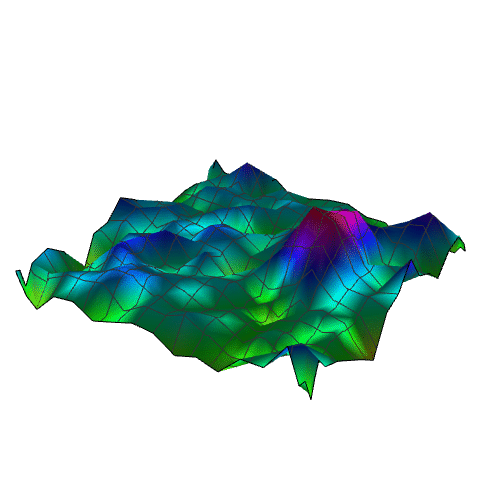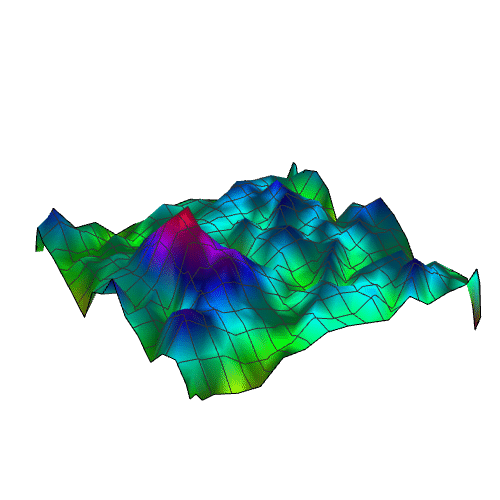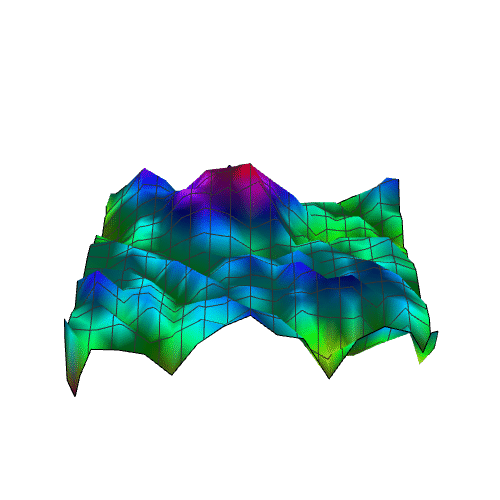
11、用这个拟合出来的曲面，来还原原来的img：

Image[Table[nihe, {x, 1, 30, 1}, {y, 1, 30, 1}]]

把图片放大到500像素，结果得到下图，与原图相差太远。