【高等几何】怎么用几何代数解决平面几何问题？

1、欧几里德空间和齐次空间是同构的，每一个欧几里德空间的点，都有唯一的齐次点与之对应，反之亦然。

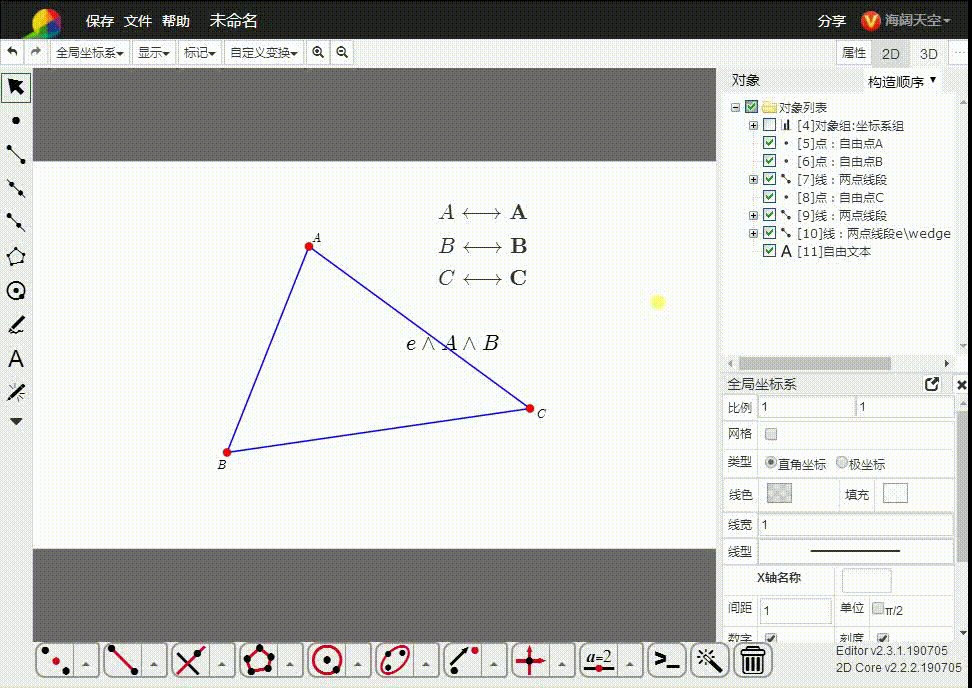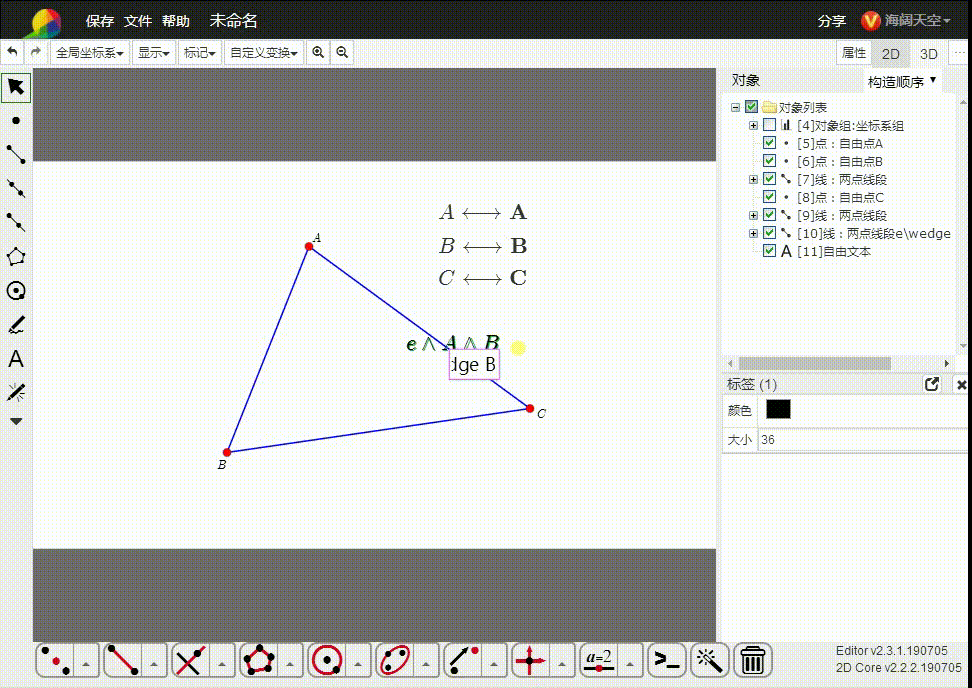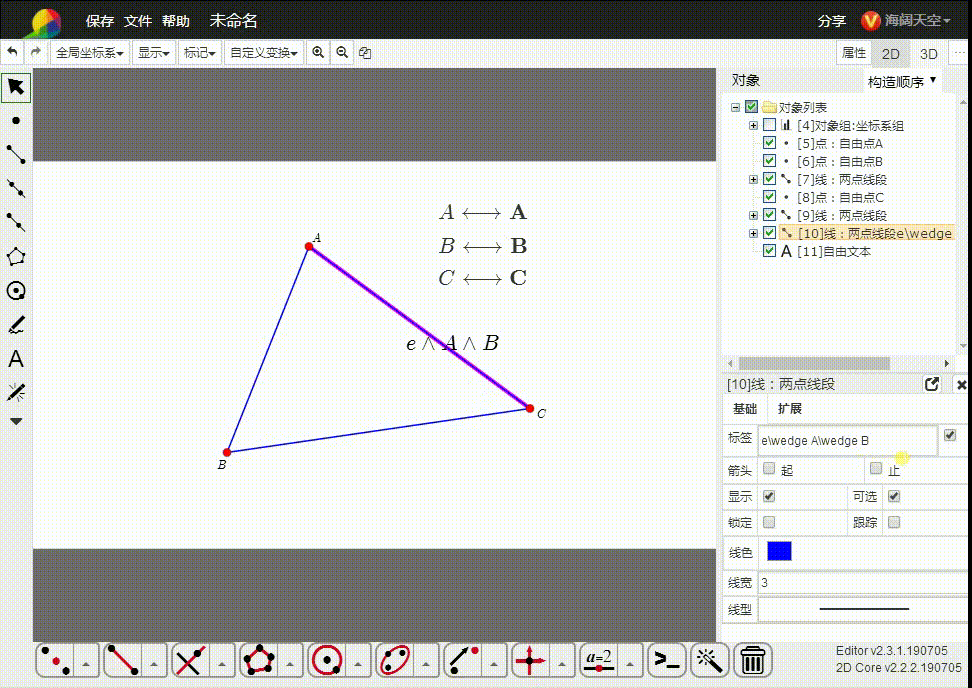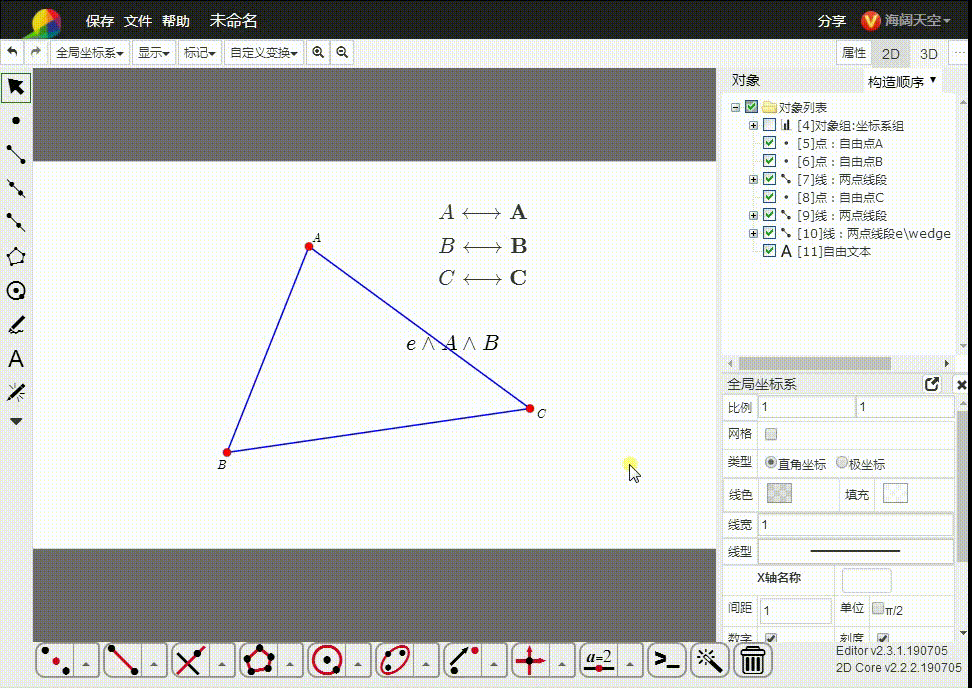
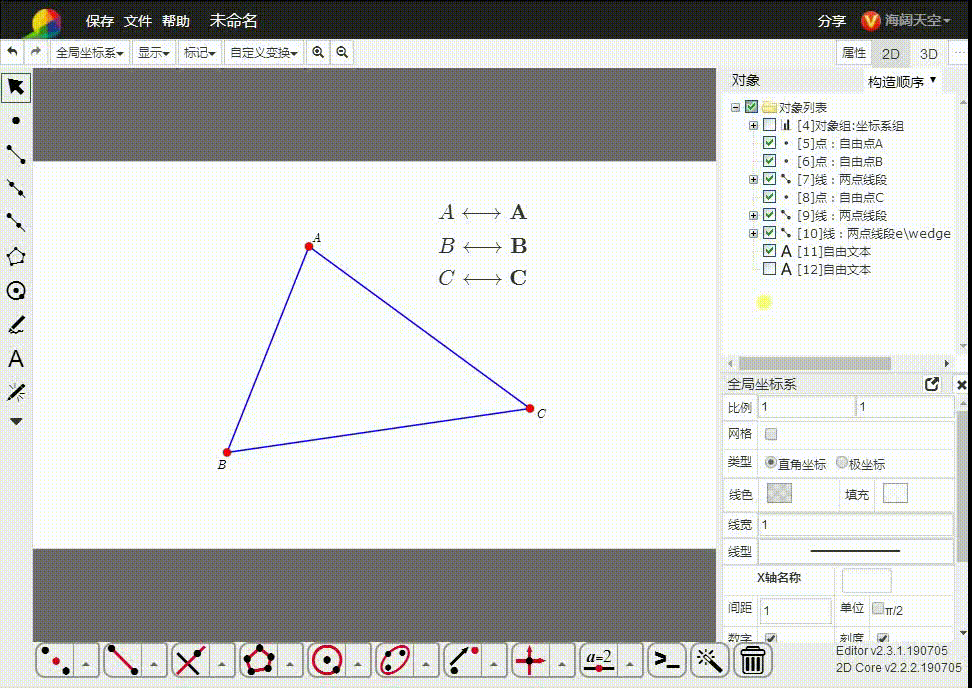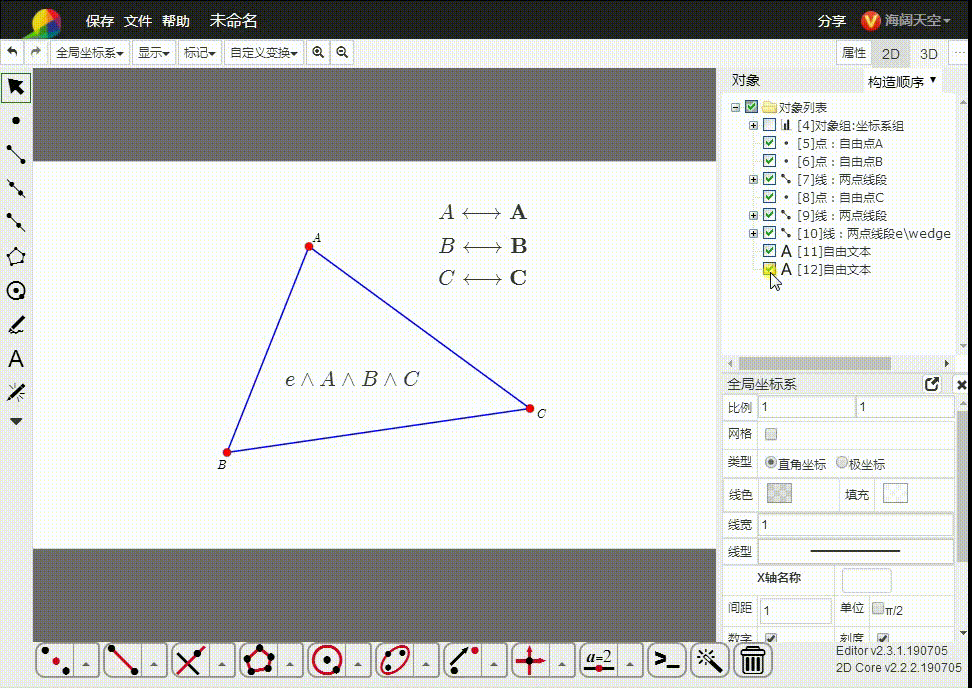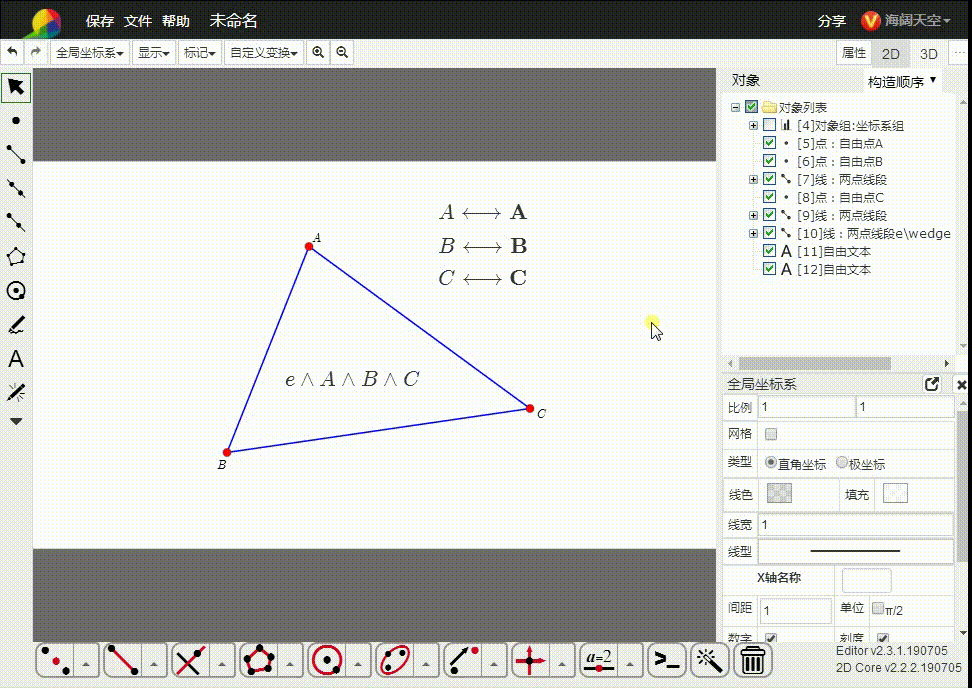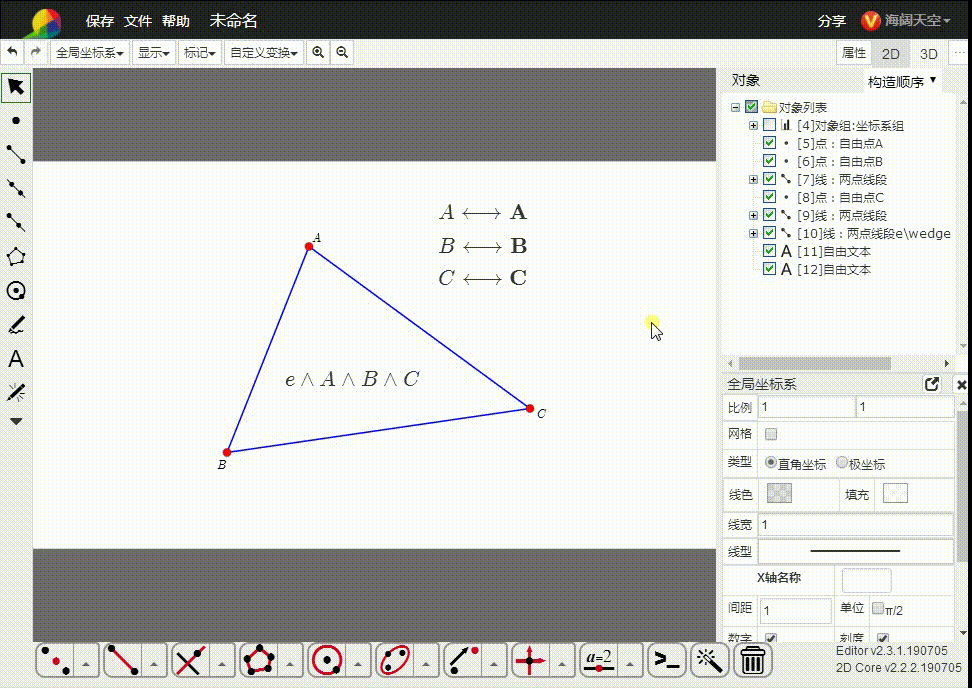
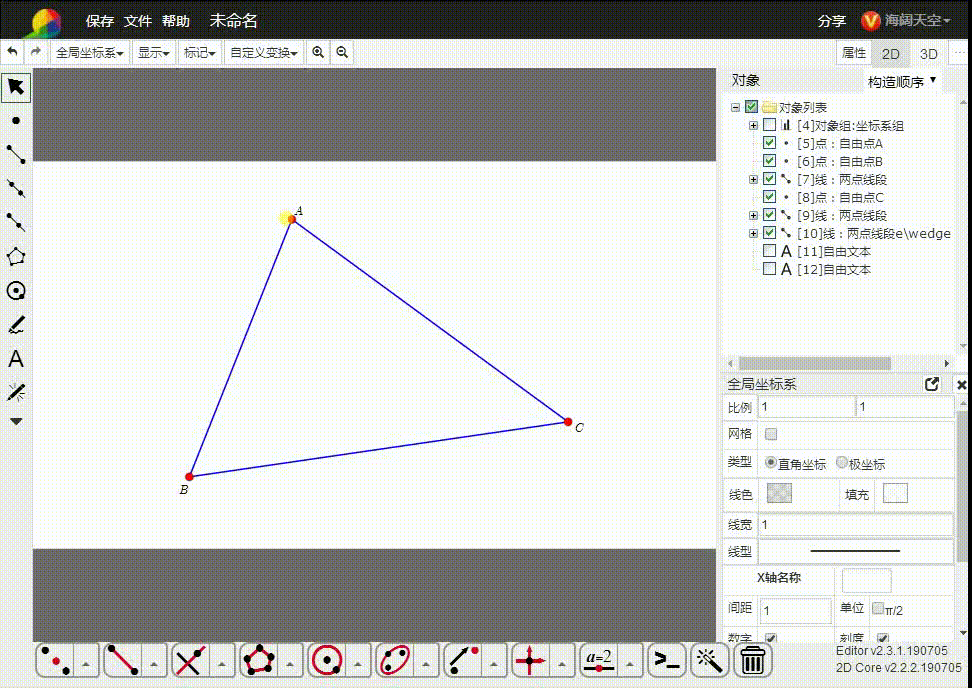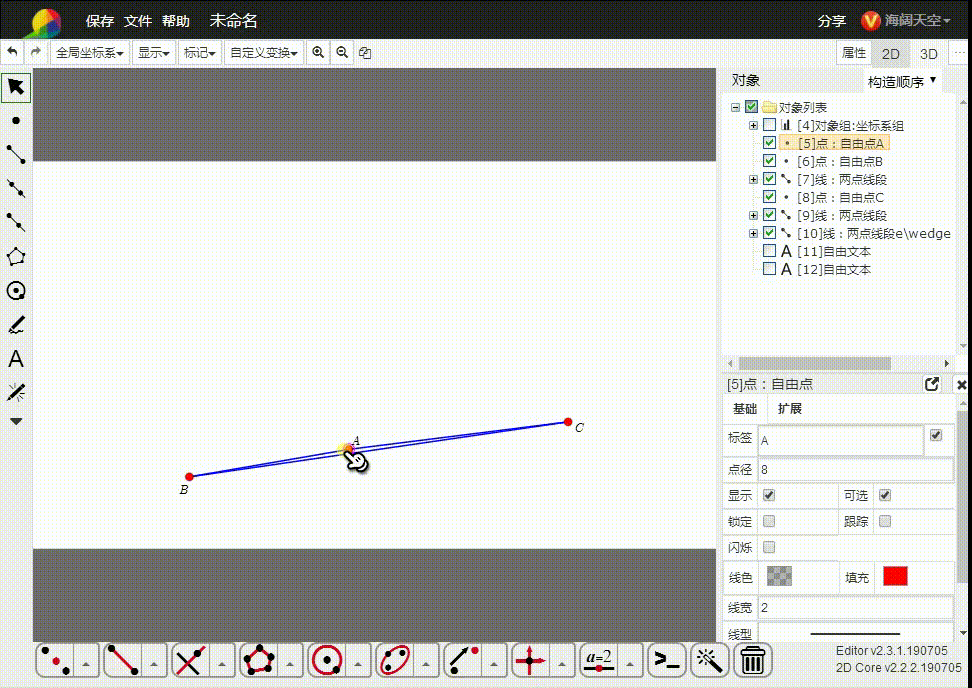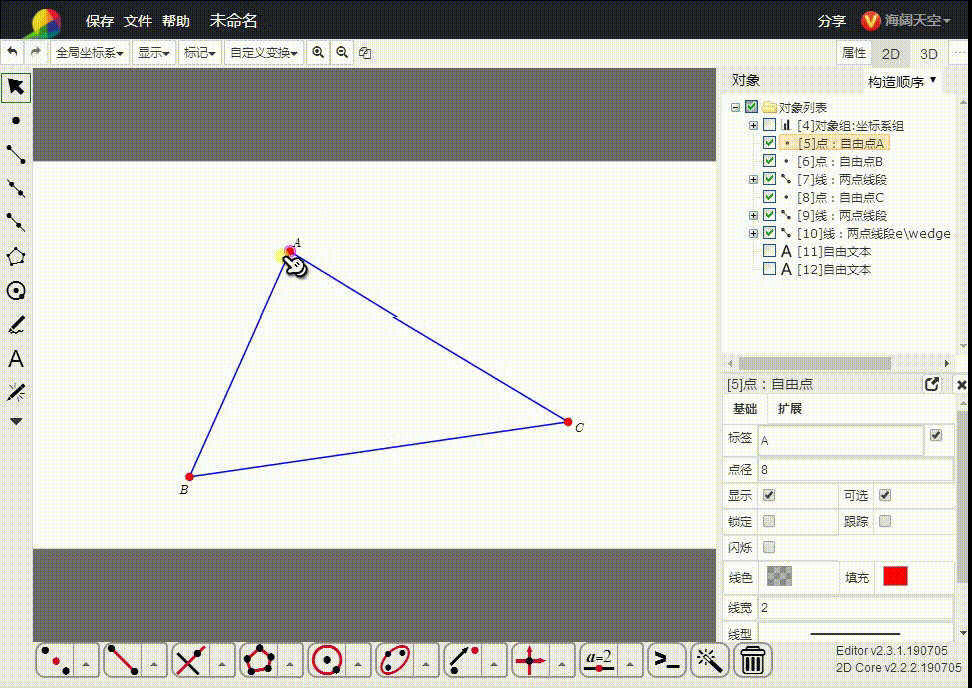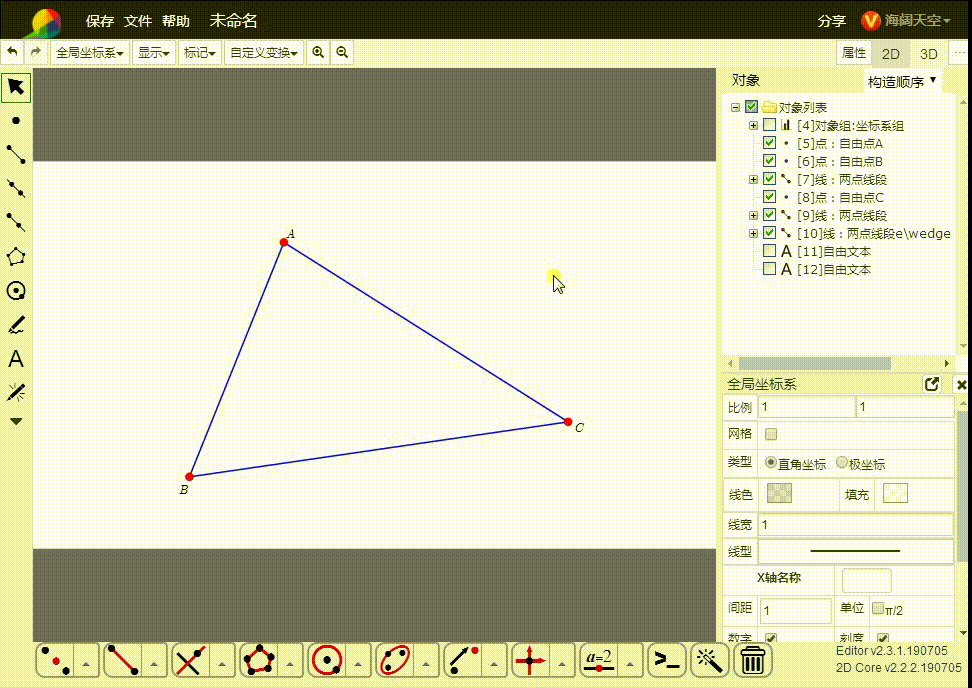
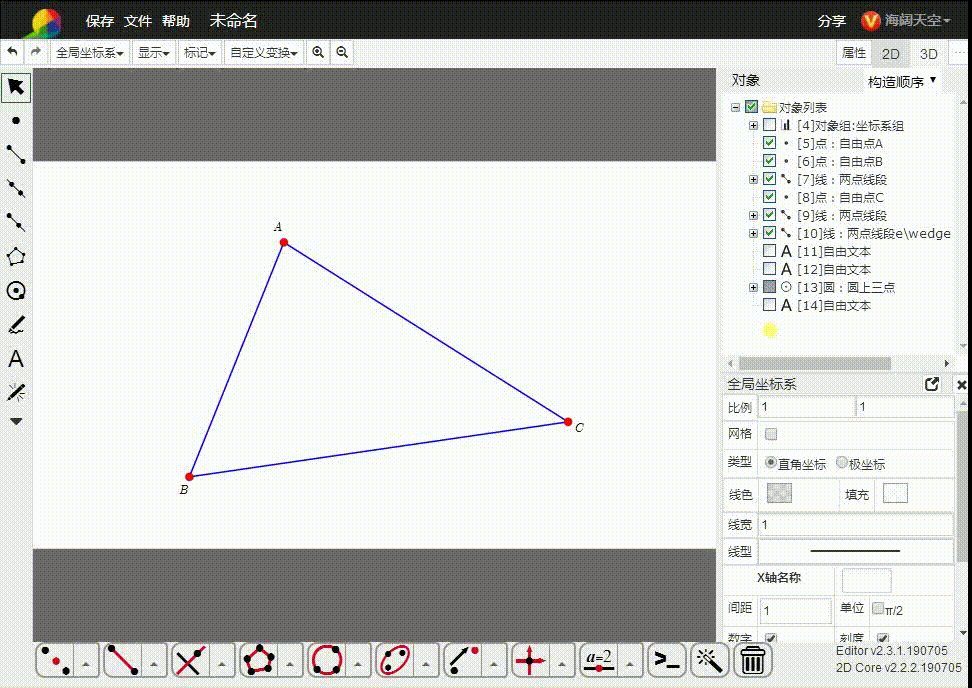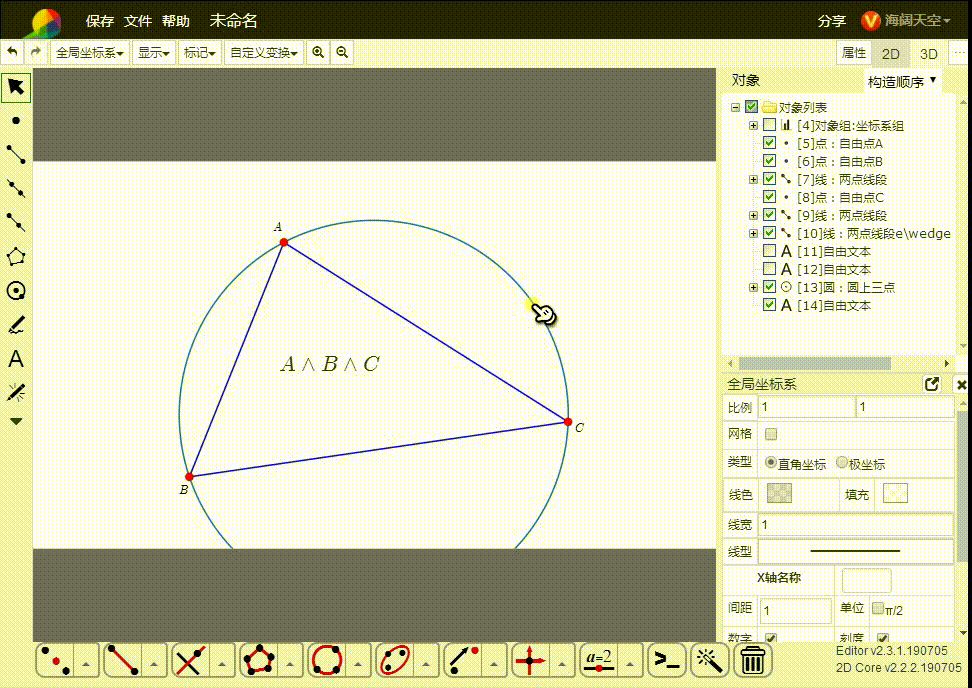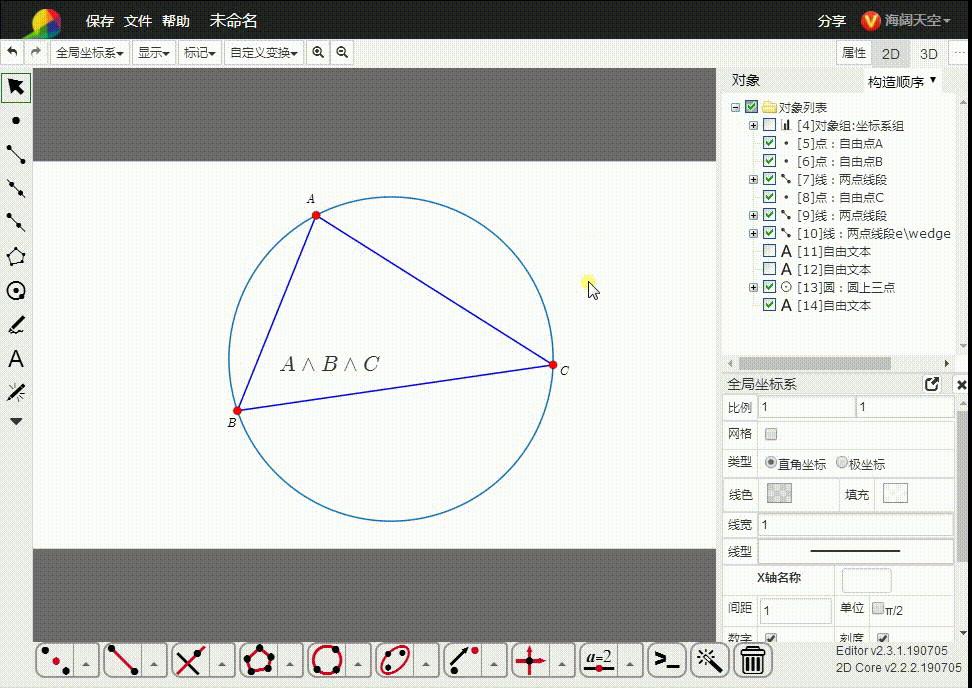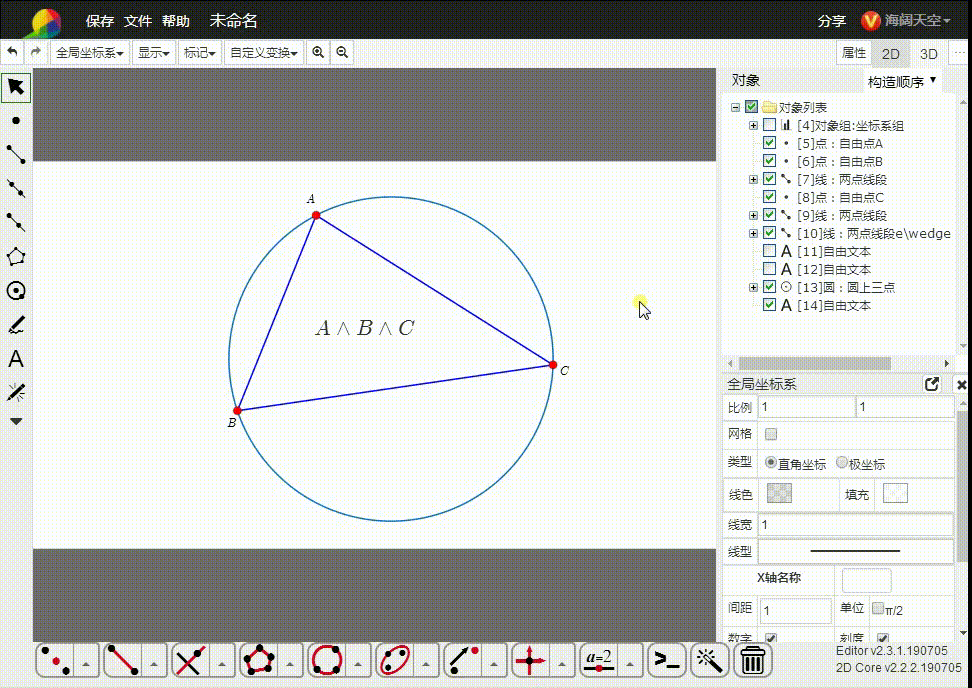
所以，我们直接把平面几何置于齐次空间里面。如图，△ABC的三个顶点都是齐次点，而A、B、C是与之对应的欧几里德空间的点。

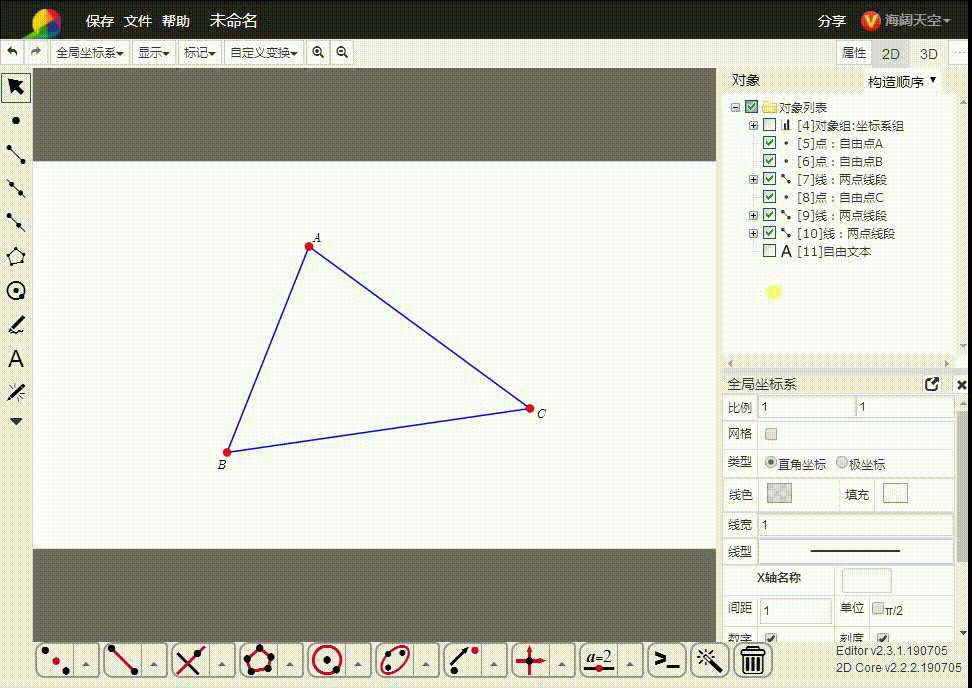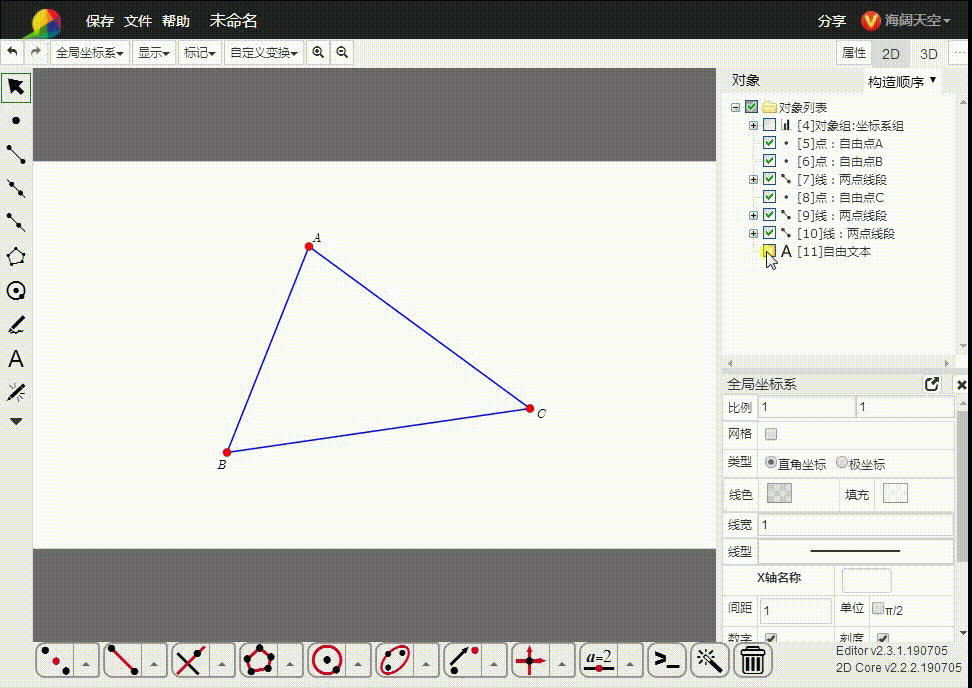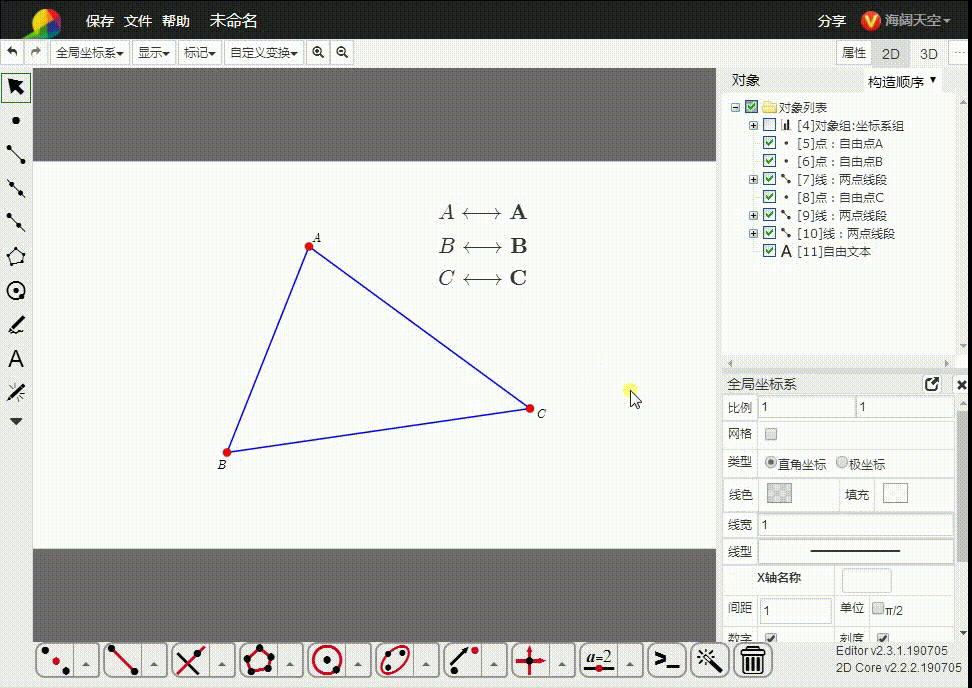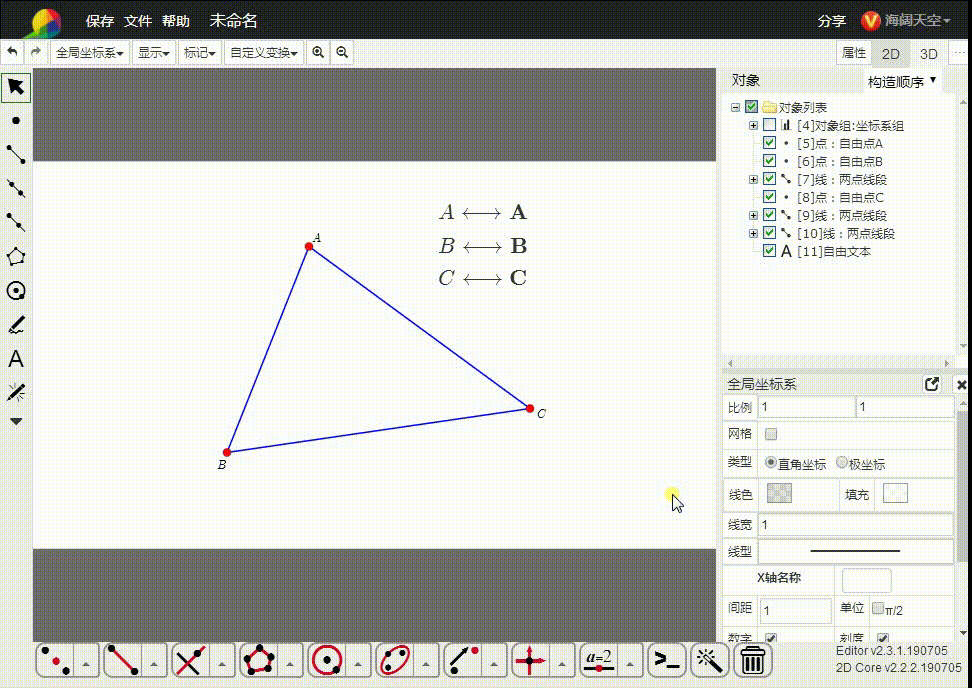
2、我们实际上是，在欧几里德空间里面添加一个与此空间正交的空向量e，扩张而成的齐次空间。可以说，齐次空间比欧几里德空间的维度大1。

这样，我们用点之间的外积来表示直线和线段：

e∧A∧B，表示经过A和B的直线，也可以表示线段AB。

这里的线段AB可以称为一维单形。

3、e∧A∧B∧C，表示由三点A、B、C确定的平面，也可以表示△ABC。

这里的△ABC是二维单形。

4、e∧A∧B 的平方，可以理解为线段AB的长度的平方。

实际上，欧几里德空间到齐次空间的变换，是等距变换。

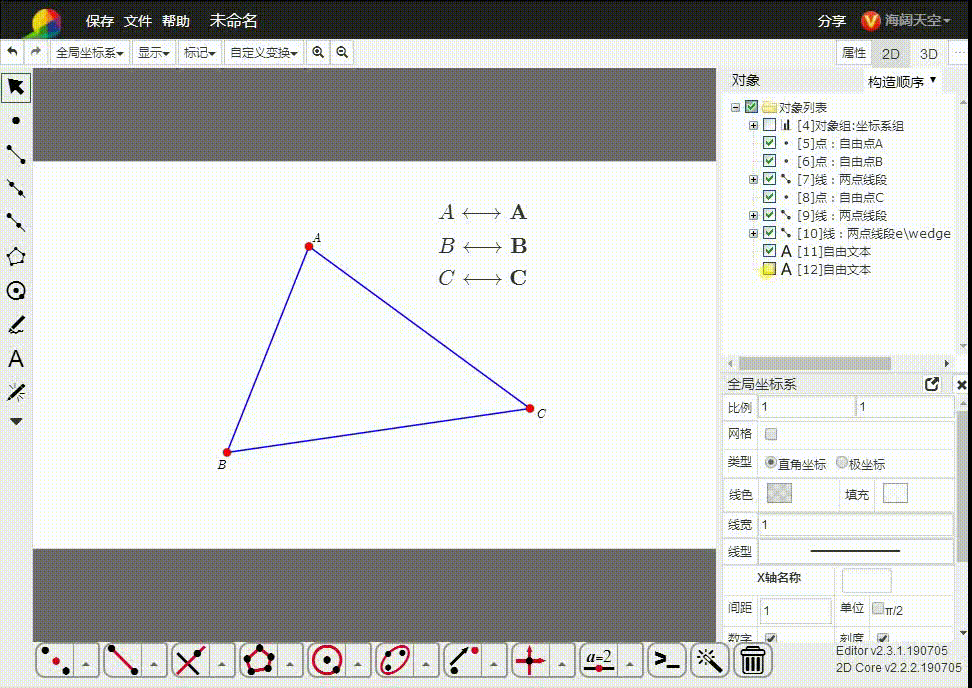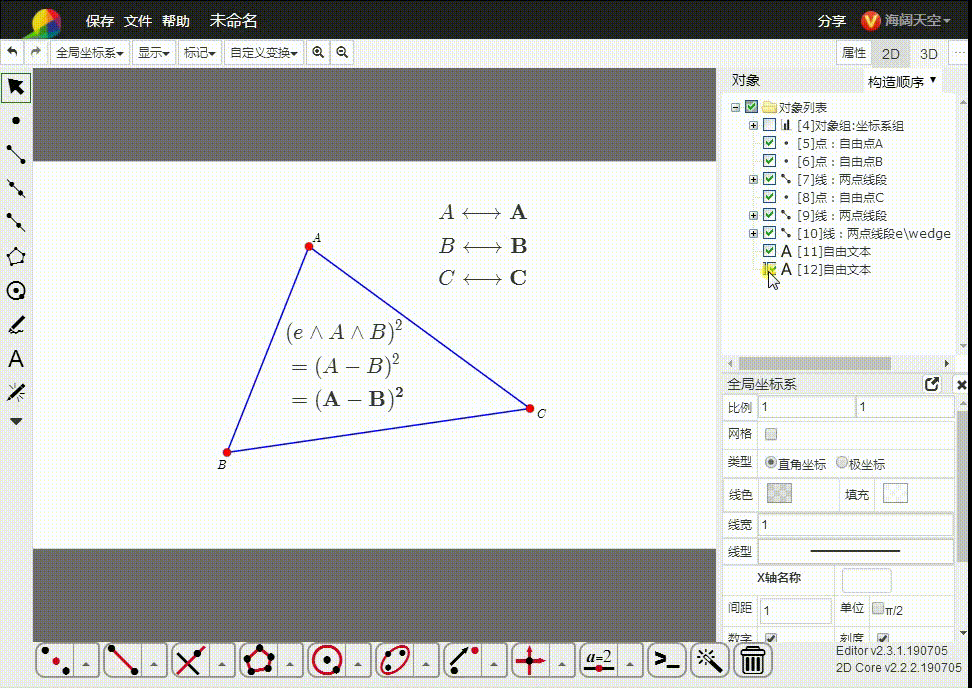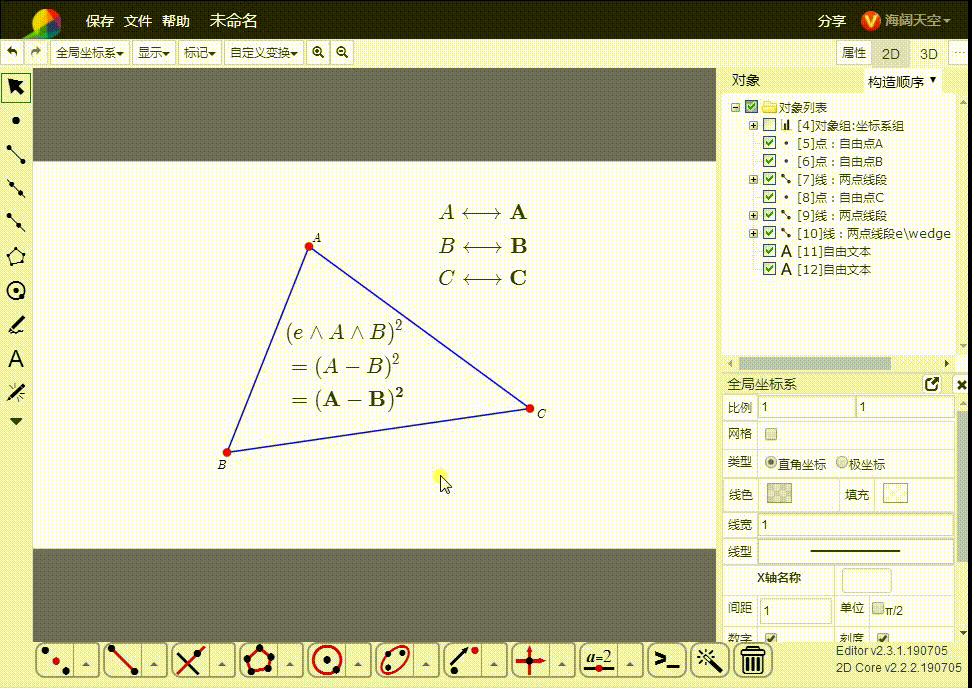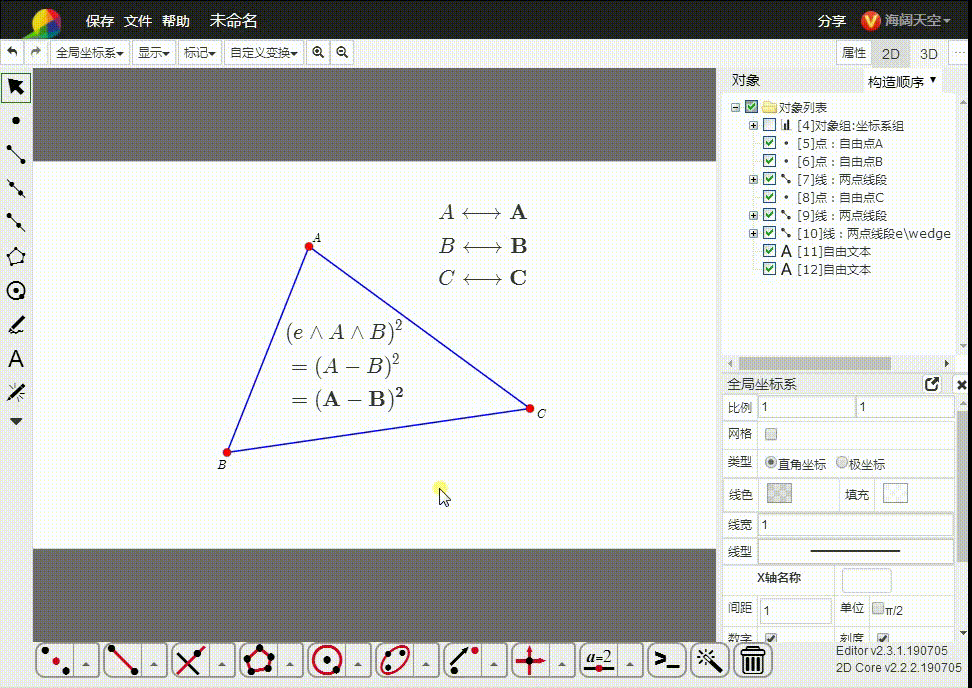
5、e∧A∧B∧C的平方，是△ABC的面积的平方。

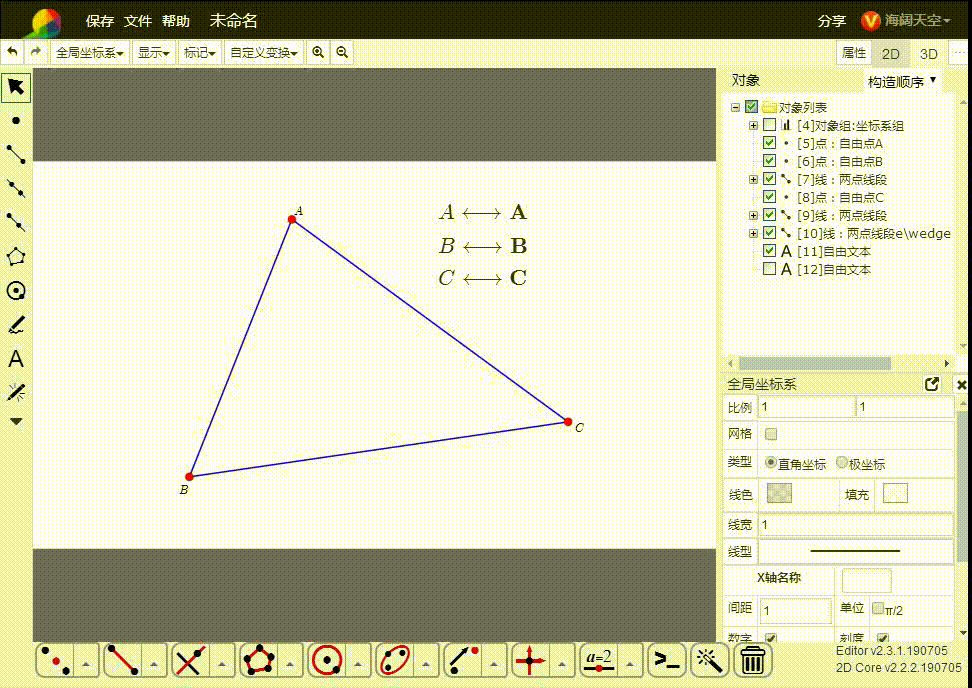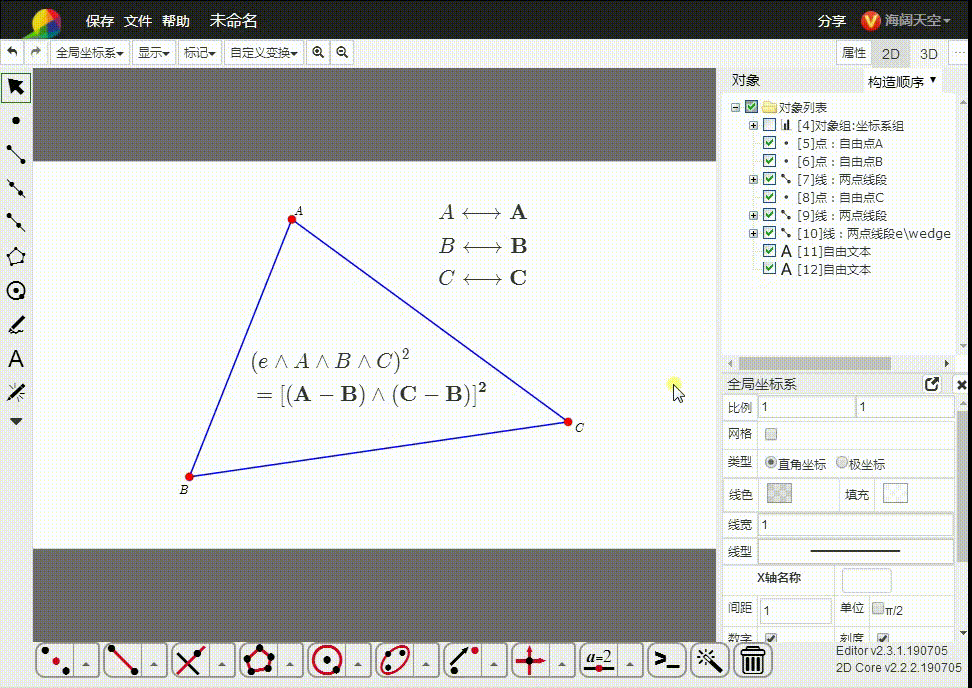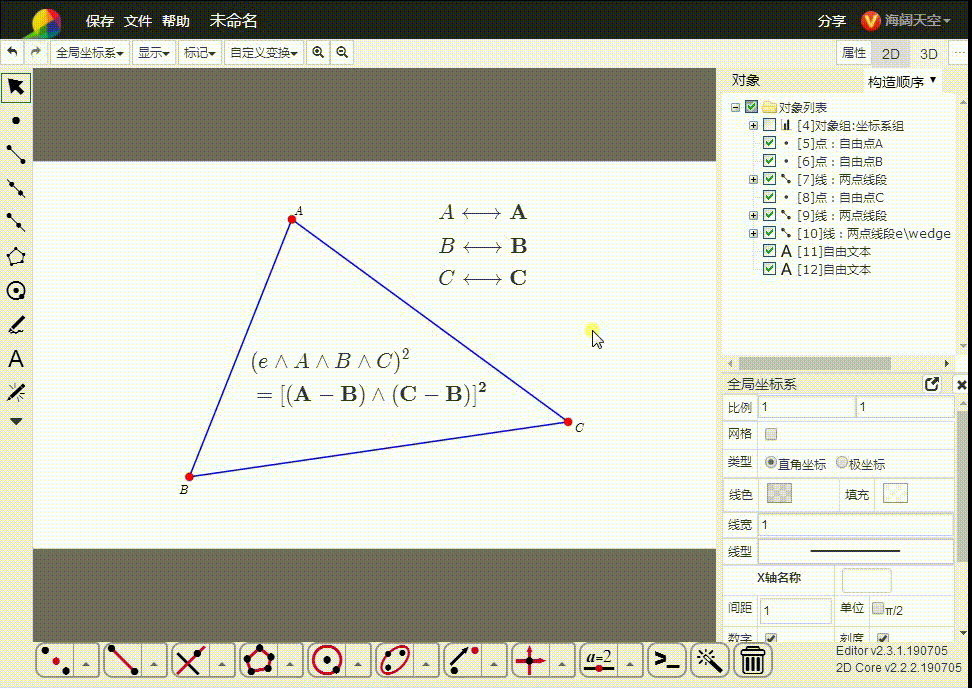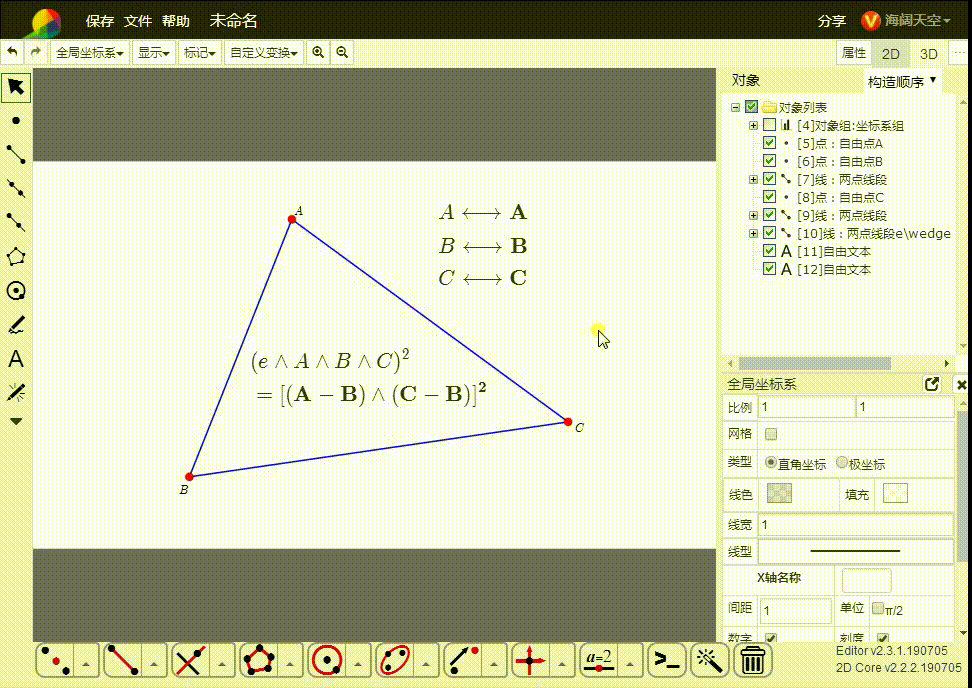
6、特殊情况是，A、B、C三点共线，e∧A∧B∧C=0（二维单形消失了，共线三点不能确定一个平面），这与△ABC面积为0是一致的。

7、A∧B∧C表示△ABC的外接圆。