训练孩子是牵引智慧的帆

1、三个三角有个空

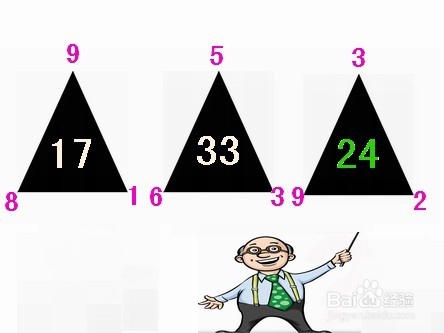
     如图，三个三角形，周围都有数字；三角形中间也有数字，就是最右边的没有，需要你填上。

     当然，外边的数字和中间的数字肯定有点关系，请你把它们的规律找出来，再计算出“？”处应该是个什么数。你能做到吗？

2、填空计算

     看出来了吗？别急，先找找规律。三角形三个角的三个数，与三角形中间的数，是有数字关系的……

     突然，你可能眼睛一亮，看出了规律：

     三角形中间的数，等于上角数加上左下角数，再与右下角数相乘。即：

     三角形中间的数=（上角数＋左下角数）×右下角数

     “？”=（3＋9）×2=24

1、残缺的算式

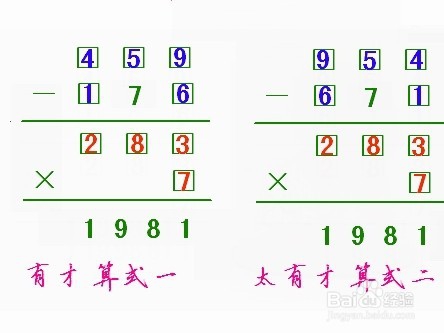
     如图，是个残缺的算式，你需要好好动动脑筋，把1、2、3、4、5、6、7、8、9这九个数分别填入“□”小方框中，使算式成立。

2、起步艰难

     我们只知道得数是“1981”，所以先要从乘法部分推导。

     看“1981”的尾数是1，乘法中只有9×9和3×7的尾数能得到“1”，9×9要用两个9，和题意不符，故取3×7。如图，3放下面为乘数，7为被乘数的尾数。

     进一步，三、七得二十一后，写1，进2，要和“1981”的“8”对上，还需要个“6”，所以被乘数中间的数字只能是2，二、三得六，加二得八，推导顺利。

     可是，再往下就不行了，什么数乘以3能得19呀？推演到此止步，如图。

3、重捋思路

     开始的思路是对的，是不是“3”和“7”的位置搞错了。如图，调整为7为乘数，3为被乘数的尾数。

     同样是三、七得二十一，写1，进2，“7”和什么数相乘尾数是“6”？只有8。所以被乘数中间的数字填写8，被乘数前面的数字填写2（只能填2）。仔细看一遍，乘法部分推导成功了！如图。

4、缜密思维

     相对而言，减法部分就容易一些。现在我们知道，还有剩下的1、4、5、6、9五个数，还知道减法部分的得数“差”是“283”。要使这个“差”的个位是3的，只能有9－6和4－1两种可能，我们分别试一试：

     ①在“被减数”的个位填写9，“减数”的个位填写6。再推导“被减数”的中间数字。什么数减7等于8？当然是15，这就确定了“被减数”中间数字是5，剩下的4和1就好办了，4填写在上面，1填写在下面，检查一遍，成功了，如图。

     ②换一换，看看能否可行。

     “被减数”的个位填写4，“减数”的个位填写1。“被减数”中间数字还是填5，剩下的9和6分别填写在上面和下面，检查一遍，也成功了，如图。

     即本题有两种填法，太有才了。

1、事出有因

     甲、乙、丙三个要好的同学放学一起回家。在途中捡到一块手表，就交给了执勤的警察。警察问他们三人是谁最先发现的手表。三个机灵的小朋友这样表述。

     甲说：“不是我发现的，也不是乙。”

     乙说：“不是我，也不是丙。”

     丙说：“不是我，我也不知道是谁发现的。”

     三个小朋友又告诉警察，他们每个人说的两句话中，都有一句是真的，一句是假的。

     这个年青的警察很聪明，马上就指出了发现手表的小朋友。

     给你10分钟，能推断是谁发现的手表吗？

2、警察神断

    警察根据每个人的话中，一句是真，一句是假，很容易推断出结果，思路如下：

     三个同学一起回家，自然发生的事情都知道。丙同学的第二句话，说他不知道是谁发现的，肯定是假话，那么，丙同学的第一句话，就是真的。也就是说丙同学不是首先发生手表的人。

     这样，乙同学“不是我，也不是丙”的话中，后半是真的，那么前面的“不是我”是假的，所以，首先发现手表的是同学乙。

你是这样思考的吗？