平行四边形的判定方法

1、1，两组对边分别平行四边形是平行四边形。平行四边形的定义为两组对边分别平行的四边形为平行四边形。所以这种方法叫做定义法。

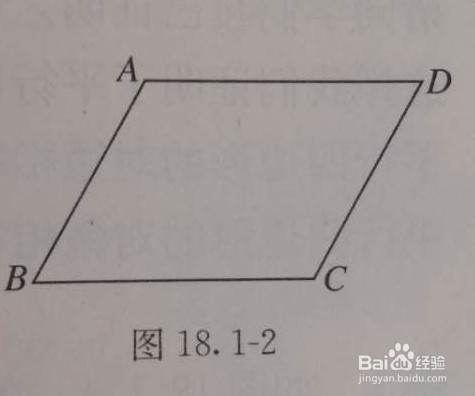
例：如图，因为AB平行于CD，AD平行于BC。

                 所以四边形ABCD为平行四边形。

2、2，对角线互相平分的四边形是平行四边形。

例：如图，在四边形ABCD中，AC,BD相交与点O，且OA=OC，OB=OD。求证：四边形ABCD是平行四边形。

证明：因为OA=OC，OB=OD，∠AOD=∠COB.

所以△AOD全等于△COB

所以∠OAD=∠OCB

所以AD平行于BC

同理AB平行于DC

所以四边形ABCD是平行四边形。

3、3，两组对边分别相等的四边形是平行四边形。

例：如图，在四边形ABCD中，AC,BD相交与点O，且AD=CB，AB=DC。求证：四边形ABCD是平行四边形。

证明：因为AD=CB，AB=DC，AC=AC。

所以△ADC全等于△CBA。

所以∠DAC=∠BCA，∠DCA=∠CAB。

所以AB平行于DC，AD平行于BC

所以四边形ABCD为平行四边形。

4、4，两组对角分别相等的四边形是平行四边形。

例：如图，在四边形ABCD中，∠A=∠C，∠B=∠D。求证：四边形ABCD是平行四边形。

证明：因为在四边形ABCD中，∠A+∠C+∠B+∠D=360°，∠A=∠C，∠B=∠D。

所以∠A+∠B=180°，∠C+∠D=180°

所以AB平行于DC，AD平行于BC。

所以四边形ABCD是平行四边形。

5、5，一组对边平行且相等的四边形是平行四边形。

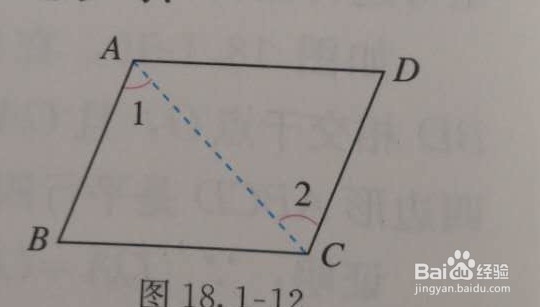
例：如图，在四边形ABCD中，AB平行于CD，AB=CD。求证：四边形ABCD是平行四边形。

证明：连接AC，因为AB平行于CD，

所以∠1=∠2.

又因为AB=CD，AC=AC,

所以△ABC全等于△CDA

所以BC=DA

所以四边形ABCD为平行四边形