位运算经典指南

1、判断奇偶数判断一个数是基于还是偶数，相信很多人都做过，一般的做法的代码如下

3、有人可能会说，我们写成 n % 2 的形式，编译器也会自动帮我们优化成位运算啊，这个确实，有些编译器确实会自动帮我们优化。但是，我们自己能够采用位运算的形式写出来，当然更好了。

4、交换两个数交换两个数相信很多人天天写过，我也相信你每次都会使用一个额外来变量来辅助交换，例如，我们要交换 x 与 y 值，传统代码如下：

6、三个都是 x ^ y，就莫名交换成功了。在此我解释下吧，我们知道，两个相同的数异或之后结果会等于 0，即 n ^ n = 0。并且任何数与 0 异或等于它本身，即 n ^ 0 = n。所以，解释如下：把（1）中的 x 带入 （2）中的 x，有y = x^y = (xy)y = x(yy) = x^0 = x。 x 的值成功赋给了 y。对于（3）,推导如下：x = x^y = (xy)x = (xx)y = 0^y = y。

8、这道题可能很多人会用一个哈希表来存储，每次存储的时候，记录 某个数出现的次数，最后再遍历哈希表，看芬简砝鬃看哪个数只出现了一次。这种方法的时间复杂度为 O(n)，空间复杂度也为 O(n)了。然而我想告诉你的是，采用位运算来做，绝对高逼格！我们刚才说过，两个相同的数异或的结果是 0，一个数和 0 异或的结果是它本身，所以我们把这一组整型全部异或一下，例如这组数据是：1， 2， 3， 4， 5， 1， 2， 3， 4。其中 5 只出现了一次，其他都出现了两次，把他们全部异或一下，结果如下：由于异或支持交换律和结合律，所以:123451234 = （11)(22)(33)(44)5= 00005 = 5。也就是说，那些出现了两次的数异或之后会变成0，那个出现一次的数，和 0 异或之后就等于它本身。就问这个解法牛不牛逼？所以代码如下

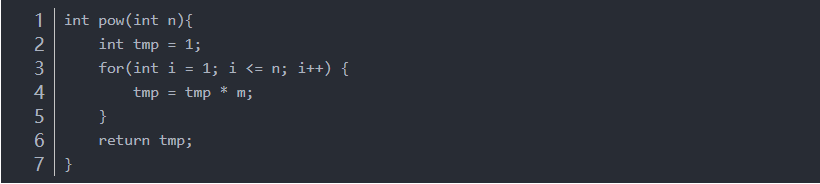
11、不过你要是这样做的话，我只能澍瘩镏舟呵呵，时间复杂度为 O(n) 了，怕是小学生都会！如果让你用位运算来做，你会怎么做呢？我举个例子吧，例如 n = 13，则 n 的二进制表示为 1101, 那么 m 的 13 次方可以拆解为:m^1101 = m^0001 * m^0100 * m^1000。我们可以通过 & 1和 >>1 来逐位读取 1101，为1时将该位代表的乘数累乘到最终结果。直接看代码吧，反而容易理解：

13、找出不大于N的最大的2的幂指数传统的做法就是让 1 不断着乘以 2，代码如下：

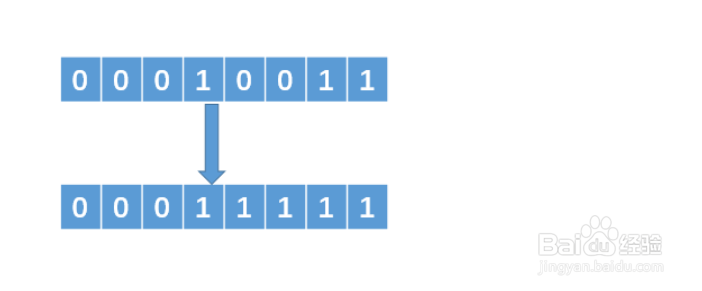
15、把得到的数值加 1，可以得到 00100000即 00011111 + 1 = 00100000。3、把 得到的 00100000 向右移动一位，即可得到 00010000，即 00100000 >> 1 = 00010000。那么问题来了，第一步中把最左边 1 中后面的 0 转化为 1 该怎么弄呢？我先给出代码再解释吧。下面这段代码就可以把最左边 1 中后面的 0 全部转化为 1，

17、这种做法的时间复杂度近似 O(1)