怎么用抽象代数的思想，解同余方程组

本文，用抽象代数的方法，来求解下面的同余方程组：3 x+4 y+5 z≡2 (mod 17)6 x+y≡5 (mod 17)2 x+10 y-z≡13 (mod 17)

工具/原料

电脑

Mathematica

初解

1、首先，这个方程组可以用矩阵的的乘法来表示：A.X==B

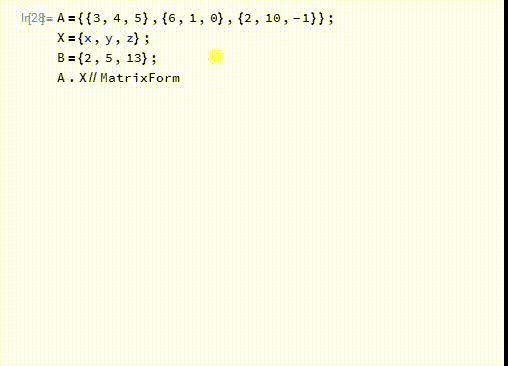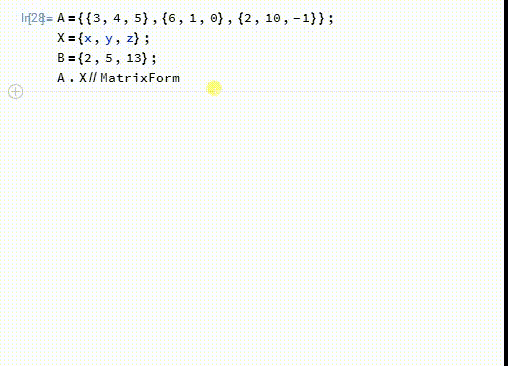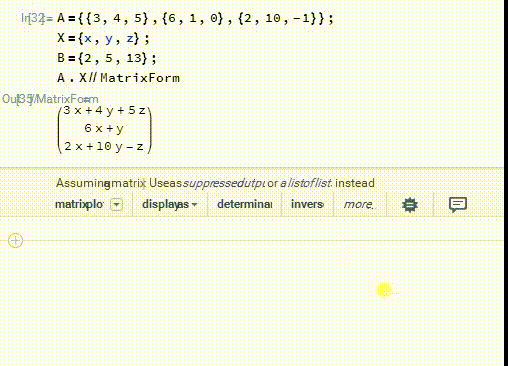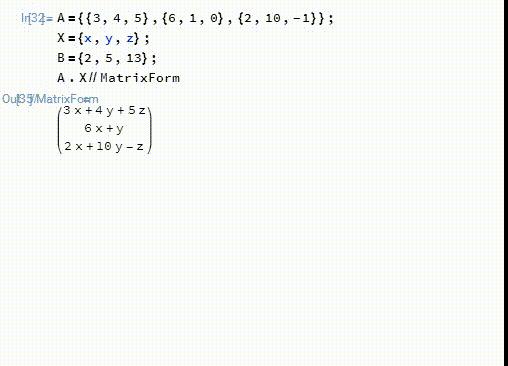
2、模17的剩余类组成一个域——F17：在这个域里面，A的逆矩阵是：A2={{16,3,12},{6,4,13},{7,12,13}}

3、那么，X就可以用矩阵乘法表示出来：X=A2.B那么答案就是X={x,y,z}={-1,-3,5}(mod 17)

检验

1、注意，上面的答案不知道出什么问题了，跟另一个方法得到的答案不一样，所以，检验答案，是必不可少的步骤。Mathematica可以直接在F17里面计算A的逆——A3，见下图。

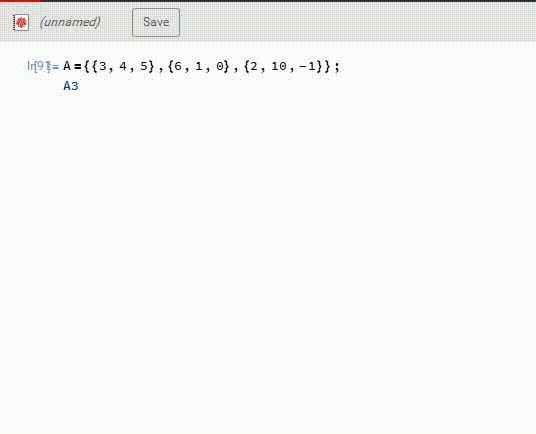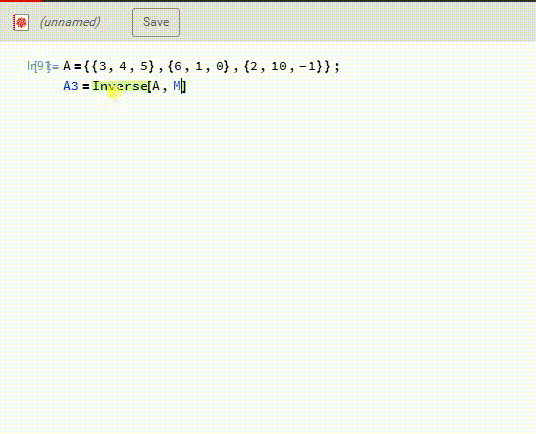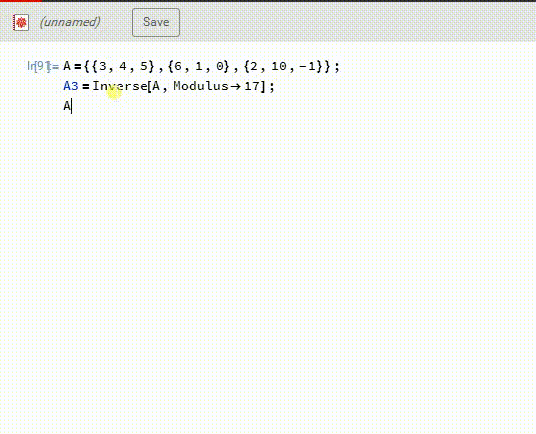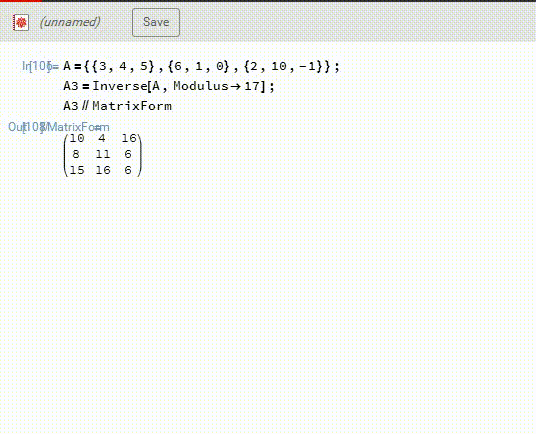
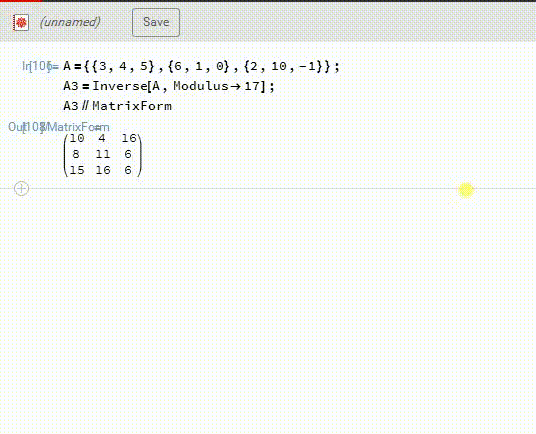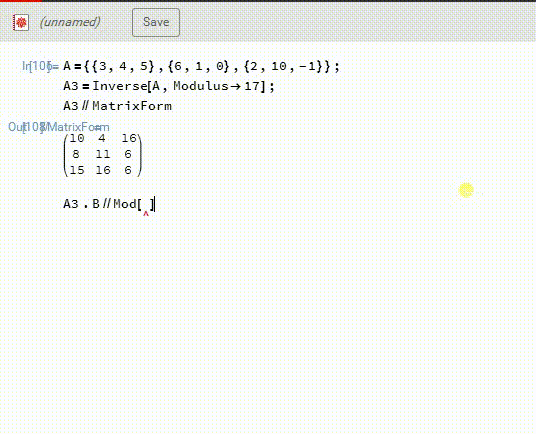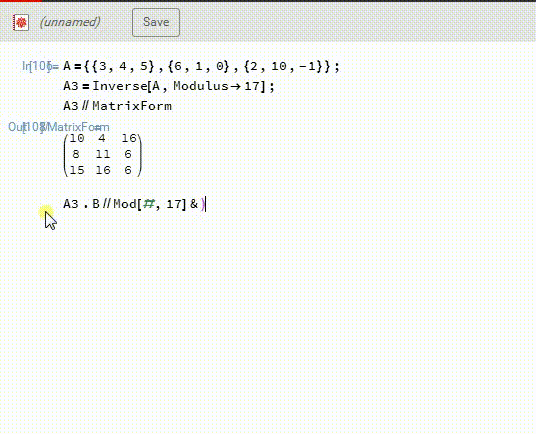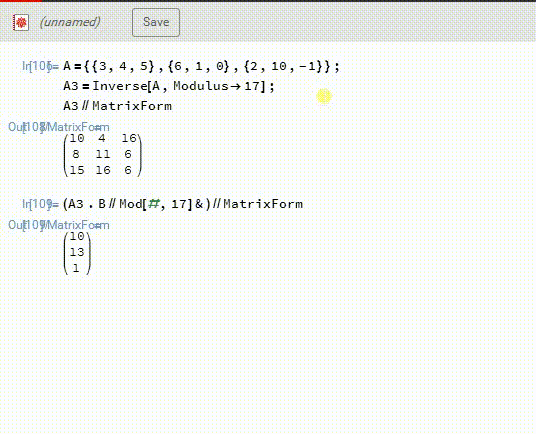
2、然后，A3.B，再模17，得到X。这一次得到的答案是X={10,13,1}，和上面的答案不相同。

再检验

1、如果两个方法得的结果不同，就需要再检验，这一次，直接用Mathematica解同余方程组：Solve[……,{x,y,z},Modulus->17]得到的答案也是X={10,13,1}。